CONTRASTES DE HIPÓTESIS

Introducción

En el Capítulo 9 se abordó una parte de la Inferencia Estadística, la referida a la Estimación Puntual y por Intervalos.

En este capítulo se abordará otra área de la Inferencia llamada Contraste (o Test) de Hipótesis.

En la Teoría de la Estimación la información que se desea conocer de la población es el valor de alguno de sus parámetros, en los Contrastes de Hipótesis se establecen procedimientos para aceptar o rechazar una hipótesis que se emite acerca de un parámetro u otra característica de la población.

Podemos considerar las siguientes etapas en el proceso:

1) El investigador formula una hipótesis sobre un parámetro poblacional, por ejemplo que toma un determinado valor

2) Selecciona una muestra de la población

3) Comprueba si los datos están o no de acuerdo con la hipótesis planteada, es decir compara la observación con la teoría

a) Si lo observado es incompatible con lo teórico entonces el experimentador puede rechazar la hipótesis planteada y proponer una nueva teoría.

b) Si lo observado es compatible con lo teórico entonces el experimentador puede continuar como si la hipótesis fuera cierta.

Se trata, en general de un proceso continuo ya que se plantean nuevas teorías y se vuelven a realizar las comparaciones.

Pero, ¿Cuándo se debe rechazar la hipótesis planteada?, ¿Cómo decidir si lo observado es compatible con lo teórico?, ¿Cuál es la probabilidad de tomar una decisión equivocada?, ¿Cuál es el error que se comete al aceptar una hipótesis falsa?, ¿Qué estadístico muestral se debe utilizar en el contraste?…. Estas y algunas preguntas más se resuelven en el estudio de los Contrastes de Hipótesis.

En resumen, el contraste de hipótesis es un procedimiento estadístico mediante el cual se investiga la verdad o falsedad de una hipótesis acerca de una característica de una población o un conjunto de poblaciones, para ello, se toman muestras representativas de la población y sobre ellas se toma la decisión acerca de la veracidad o falsedad de la hipótesis planteada.

Se distingue entre dos tipos de contrastes: Contraste de Hipótesis Paramétrico y Contraste de Hipótesis No-Paramétrico:

Contraste de Hipótesis Paramétrico:

Conocida una v.a. con una determinada distribución, se establecen afirmaciones sobre los parámetros de dicha distribución. Por ejemplo, dada una m.a.s. \( X_1, X_2, \cdots, X_{n} \) de una v.a.  \( X \rightarrow  N(μ, σ) \) establecemos la afirmación μ=20

Contraste de Hipótesis No-Paramétrico:

La distribución de las observaciones es desconocida a priori y las afirmaciones que se establen son acerca de alguna propiedad de la distribución que se muestrea. Ejemplos: Una v.a. \( X \) tiene una distribución Normal; Dos vv.aa. \( X \) e \( Y \) son independientes; Dos muestras independientes proceden de la misma población…

Conceptos básicos

En un problema de contraste de hipótesis hay una teoría preconcebida sobre alguna característica de la población que se estudia, por ejemplo, el contenido medio de proteínas de un preparado alimenticio es de 42%; el número de eritrocitos por milímetro cúbico de sangre sigue una distribución Normal; los calmantes A y B son igual de efectivos en el tratamiento de la jaqueca. Esto nos conduce a que en cualquier estudio estadístico hay dos teorías o hipótesis implícitas: la hipótesis que propone el experimentador y la negación de esta hipótesis. La primera hipótesis recibe el nombre de Hipótesis Alternativa y se denota por \( H_1 \), mientras que la segunda hipótesis recibe el nombre de Hipótesis Nula y se denota por \( H_0 \). El objetivo del problema de contraste es decidir si el procedimiento realizado tiende a apoyar o a rechazar la Hipótesis Nula.

La hipótesis \( H_0 \) es la hipótesis de la “no diferencia”, es decir, la igualdad forma parte de \( H_0 \). Así, en el ejemplo sobre el contenido medio de las proteínas, la afirmación de que \(  μ=42 \) forma parte de \( H_0 \) y se escribe como

\( H_0 \equiv μ=42 \)

Esta hipótesis que asigna, que especifica, un valor particular para el parámetro en estudio recibe el nombre de Hipótesis Sencilla o Simple.

Si la hipótesis nula se escribe como

\( H_0 \equiv μ \leq 42  \hspace{.2cm} \) o \( \hspace{.2cm} H_0 \equiv μ \geq 42 \)

no asigna ningún valor específico al parámetro y recibe el nombre de Hipótesis Compuesta.

Para construir una regla de decisión apropiada en el contraste de hipótesis, como hemos dicho anteriormente, es necesario establecer una hipótesis alternativa que muestre el “posible valor” del parámetro de interés si la hipótesis nula es falsa. Generalmente la hipótesis alternativa es la negación de la hipótesis nula: El contenido medio de proteínas de un preparado alimenticio no es de 42%; el número de eritrocitos por milímetro cúbico de sangre no sigue una distribución Normal; los calmantes A y B no son igual de efectivos en el tratamiento de la jaqueca. La hipótesis alternativa puede ser simple o compuesta. En muchas ocasiones, aunque no es una generalización, la hipótesis H₀ se establece más específica que la \( H_1 \).

Un Contraste o Test de Hipótesis es un procedimiento mediante el cual nos decidimos por \( H_0 \) o por \( H_1 \). Las hipótesis estadísticas se formulan con el propósito, siempre que sea posible, de rechazar \( H_0 \) y por lo tanto, aceptar \( H_1 \). Es importante comprender que una decisión con respecto a una hipótesis estadística es un proceso inferencial, el cual siempre se encuentra sujeto a error.

Antes de continuar introduciendo más conceptos vamos a considerar por ejemplo, que deseamos probar que la media poblacional tiene un determinado valor y establecemos la hipótesis nula: \( H_0 \equiv μ=μ_0 \).

Para ello tomamos una muestra de la citada población y con base en la muestra calculamos la media muestral \(  \bar {x} \). Si el valor de la media muestral está próximo al valor de la media poblacional entonces no se rechaza \(  H_0 \), pero, ¿Cómo de próxima? ¿Qué error es admisible? Parece intuitivamente razonable que si el intervalo de confianza para \( μ \) contiene a x entonces no se rechaza \( H_0 \)  y se rechaza en caso contrario. Así,

• Si \(  X \in \left [μ_0-z_{α/2}(σ/\sqrt{n}) , μ_0+z_{α/2}(σ/\sqrt{n}) \right ]  \Rightarrow  \hspace{.2cm} \)  No rechazar \(  \hspace{.2cm} H_0 \)
• Si \(  X \notin \left [μ_0-z_{α/2}(σ/\sqrt{n}) , μ_0+z_{α/2}(σ/\sqrt{n}) \right ]  \Rightarrow  \hspace{.2cm} \)  Rechazar \(  \hspace{.2cm} H_0 \)

Nota: No rechazar la Hipótesis nula en el sentido de que \( μ_0  \) es un valor posible de \( μ  \) pero hay otros valores igualmente posibles.

Ejemplo 10.1. En una cadena de hoteles se determinó que el número medio de llamadas solicitando servicio era de 42 por día. Para comprobar su afirmación se revisaron los re-gistros de servicios para 25 días seleccionados al azar. Estudios realizados con anterioridad dieron una desviación típica σ=6. Si α=0.05 ¿Se puede rechazar la hipótesis con base en estos datos de la muestra?. (Supuesto que la población estudiada es Normal).

Respuesta:

Sabemos que \( μ_0=42 \hspace{.2cm}, \hspace{.2cm} n=25 \hspace{.2cm} ,  \hspace{.2cm} σ=6 \), por lo que

\( X \rightarrow N(42; 6/ \sqrt {25})=(42; 1.2) \)

Para un nivel de significación del 5%, \( z_{α/2}=1.96 \) y el intervalo de no rechazo o región de no rechazo para \( μ \) es: \( (42-1.96 \times 1.2 , 42+1.96 \times 1.2)=(39.648 , 44.352) \). Entonces:

• Si \( x \in (39.648 , 44.352) \) no se rechaza la hipótesis de que el número medio de llamadas al día es 42.
•  Si \( x \notin (39.648 , 44.352) \) se rechaza la hipótesis de que el número medio de llamadas al día es 42.

Pero, puede suceder que:

1) La media muestral no pertenezca al intervalo y sin embargo el valor de μ sea 42. Cometiendo por tanto el error de rechazar la hipótesis nula cuando es cierta. En este ejemplo, el riesgo de cometer este error es α=0.05

2) La media muestral pertenezca al intervalo y sin embargo el valor de μ sea 40. Cometiendo por tanto el error de no rechazar la hipótesis nula cuando es falsa, ya que aunque la media muestral pertenezca al intervalo la decisión de no rechazar la hipótesis no es la correcta.

En cada una de estas situaciones estamos ante un tipo de error que vamos a analizar pero, veamos en primer lugar las posibles decisiones que se pueden tomar con respecto a \( H_0 \)

Rechazar \( H_0  \left \{ \begin{array} \\ Cuando \hspace{.1cm} H_0 \hspace{.1cm} es \hspace{.1cm} cierta \\  Cuando \hspace{.1cm} H_0 \hspace{.1cm} es \hspace{.1cm} falsa \end{array} \right. \hspace{.3cm} \)  o \( \hspace{.3cm}\)  No rechazar \( H_0  \left \{ \begin{array} \\ Cuando \hspace{.1cm} H_0 \hspace{.1cm} es \hspace{.1cm} cierta \\ Cuando \hspace{.1cm} H_0 \hspace{.1cm} es \hspace{.1cm} falsa \end{array} \right. \)

a) Si se rechaza \( H_0 \) puede suceder que:

– Se rechace algo que es cierto siendo la decisión incorrecta o
– Se rechace algo que es falso siendo la decisión correcta

b) Si no se rechaza \( H_0  \) puede suceder que:

– No se rechace algo que es cierto siendo la decisión correcta o
– No se rechace algo que es falso siendo la decisión incorrecta.

Existiendo, por tanto dos posibilidades de tomar una decisión equivocada y esto nos conduce a definir los dos tipos de error que se pueden cometer

Error de Tipo I o error α consiste en rechazar la hipótesis \( H_0  \) cuando es cierta y se define como

 \( P[rechazar \hspace{.1cm} H_0 / H_0 \hspace{.1cm} es \hspace{.1cm} cierta]=α \hspace{.1cm}; \hspace{.1cm} 0 \leq α \leq 1 \)

Error de Tipo II o error β consiste en no rechazar la hipótesis \( H_0  \) cuando es falsa y se define como

 \( P[no\hspace{.1cm}  rechazar \hspace{.1cm} H_0 / H_0 \hspace{.1cm} es \hspace{.1cm} falsa] =β \hspace{.1cm} ; \hspace{.1cm} 0 \leq β \leq 1  \)

En la tabla siguiente presentamos las decisiones y posibles errores que se pueden cometer

\(  \begin{array}{||l|cc||} \hline &  \hspace{5cm} Decisión   \\ \hline & Rechazar \hspace{.1cm}  H_0 & No \hspace{.1cm}  rechazar H_0 \\ \hline Hipótesis \hspace{.1cm} cierta \hspace{.1cm} H_0 & α & Decisión \hspace{.1cm} correcta \\ \hline Hipótesis \hspace{.1cm} falsa \hspace{.1cm} H_0 & Decisión \hspace{.1cm} correcta & β \\ \hline \end{array}  \)

Tabla  10.1

Vamos a determinar el error \( \beta \)  en el Ejemplo 10.1, suponiendo que el valor de la media poblacional no es 42 sino 40, entonces \(  X \rightarrow N(40; 1.2) \)

\( \begin{array}{ll} \beta  = & P[no \hspace{.1cm} rechazar \hspace{.1cm} H_0 / H_0 \hspace{.1cm} es \hspace{.1cm} falsa]=P[39.648 \leq X \leq 44.352/μ=40] = \\  & = P \left [ \displaystyle \frac {39.648-40}{1.2} \leq \displaystyle \frac {X-40} {1.2} \leq \displaystyle \frac {44.352-40} {1.2} \right ]=P[-0.293 \leq Z \leq 3.627]  =\\  & = 1-P[Z>3.627]-P[Z>0.293]=1-0.0001-0.3859=0.614  \\  \end{array}  \)

El error β es 0.614, por lo tanto el área comprendida entre 39.648 y 44.352 vale 0.614, es decir que de cada 100 muestras que tomemos en la población:

∙ En 61 de ellas cometemos un error de tipo II, es decir, admitimos como cierta una hipótesis que es falsa
∙ En 39 de ellas admitimos como verdadera una hipótesis que es cierta.

A continuación, estudiamos la relación entre los dos tipos de error entre sí y la relación con el tamaño de la muestra:

a) Si disminuye el error de tipo I

Supongamos que el Ejemplo 10.1, el nivel de significación es α=0.01.

Entonces la región de no rechazo es:

\( (42-2.58 \times 1.2 , 42+2.58 \times 1.2)=(38.904 , 45.096) \) y su amplitud es igual a 6.192.

Por lo tanto, la disminución de α hace que aumente la región de no rechazo.

Veamos que sucede con el error β

\( \begin{array}{ll} \beta  = & P \left [\displaystyle \frac {38.904-40} {1.2} \leq  \displaystyle \frac {X-40} {1.2} \leq \displaystyle \frac {45.096-40} {1.2} \right ]=P[-0.914 \leq  Z \leq 4.247] =\\  & =1-P[Z>4.247]-P[Z>0.914]=1-0.1814=0.8186 \\  \end{array}  \)

Por lo tanto, con un tamaño fijo de muestra, si disminuye el error α de 0.05 a 0.01 entonces el error β aumenta de 0.614 a 0.8186. Del mismo modo se comprueba que un aumento del error α conlleva a una disminución del error β.

b) Si aumenta el tamaño muestral

En este caso la distribución en el muestreo presentará menos variabilidad y el error de tipo II decrece.

En efecto, supongamos que en el Ejemplo 10.1 el tamaño de la muestra es 36.

b1) Para α=0.05 la región de no rechazo es: (40.04 , 43.96) y el error β es

\(  \beta =P[40.04-40 \leq Z \leq 43.96-40]=P[0.04 \leq Z \leq 3.96]= 1-0.4840=0.516 \)

b2) Para α=0.01 la región de no rechazo es: (39.42 , 44.58) y el error β es

\(  \beta =P[39.42-40 \leq Z \leq 44.58-40]=P[-0.58 \leq Z \leq 4.58]= 1-0.291=0.709 \)

\(  \begin{array}{||l|c|c|c|c||} \hline & α & R. \hspace{.1cm}No \hspace{.1cm} rechazo & Amplitud  & β \\ \hline
n=25 & 0.05 & (39.648 , 44.352) &  4.704 & 0.614 \\ \hline
n=25 & 0.01 & (38.904 , 45.096) & 6.192 & 0.8186 \\ \hline
n=36 & 0.05 & (40.04 , 43.96) & 3.92 &  0.516 \\ \hline
n=36&  0.01 & (39.42 , 44.58)  & 5.16 &  0.709 \\ \hline \end{array}  \)

Como hemos dicho anteriormente un contraste de hipótesis es un procedimiento para decidir si se rechaza la hipótesis \( H_0 \) basándonos en una muestra aleatoria tomada de la población bajo estudio. La decisión se toma observando el valor de algún estadístico cuya distribución de probabilidad, bajo la presunción de que \( H_0 \) es cierta, se conoce. Dicho estadístico recibe el nombre de Estadístico de Contraste. Si el valor del estadístico cuando \( H_0 \) es cierta difiere de lo esperado, rechazamos la hipótesis nula en favor de la hipótesis alternativa; en caso contrario no rechazamos la hipóteis nula.

Los valores del estadístico de contraste que nos conducen a rechazar la hipótesis \( H_0 \) forman la Región Crítica o Región de Rechazo del contraste (los puntos que delimitan la región crítica se llaman Puntos Críticos) y los valores que nos conducen a decidir \( H_0 \) forman la Región de No rechazo.

Se dice que el resultado de un test o contraste de hipótesis es Estadísticamente Significativo cuando se rechaza \( H_0 \) y se dice que es Estadísticamente No-Significativo cuando no se rechaza \( H_0 \).

En este capítulo estudiamos los Contrastes Paramétricos, es decir los contrastes que se refieren a un parámetro \( \theta \).

En términos generales: Dada una variable aleatoria \( X  \) que se distribuye según una ley de probabilidad \( Ϝ(\theta)  \) que depende de un parámetro θ. Supongamos que el parámetro \( \theta \) es desconocido y que \( \theta_0 \) es el valor propuesto para \( \theta \). El contraste consiste en elegir, en alguno de los contrastes siguientes, entre la hipótesis \( H_0  \) o \( H_1 \).

\(  \begin{array}{ccccc} H_0 \equiv  \theta \leq \theta_0 & o &  H_0 \equiv θ \geq θ_0  & o & H_0 \equiv θ = θ_0 \\ H_1 \equiv  \theta > \theta_0  & o  &  H_1 \equiv  θ < θ_0  & o &  H_1 \equiv  θ \neq θ_0 \end{array}  \)

Nota: Consideramos la hipótesis \( H_0  \) simple y la hipótesis \( H_1  \) compuesta.

• En los dos primeros contrastes, en los que la hipótesis alternativa es: \( H_1≡ θ>θ_0 \)  o \(  H_1 ≡ θ<θ_0 \), se dice que la Hipótesis Alternativa es Unilateral, ya que los posibles valores de \(  θ \)  bajo \( H_1 \) están situados a un lado del valor propuesto bajo \(  H_0 \)  y la región crítica recibe el nombre de Región crítica o de Rechazo Unilateral. (La hipótesis \(  H_1 \)  da lugar a una región crítica a un solo lado del valor del parámetro).
• En el tercer contraste, en el que la hipótesis alternativa es de la forma \(  H_1≡ θ \neq θ_0 \), se dice que la Hipótesis Alternativa es Bilateral y la región crítica también recibe el nombre de Región Crítica Bilateral. (La hipótesis \(  H_1 \) da lugar a una región crítica a ambos lados del valor del parámetro).

Potencia de un contraste:

Se define la Potencia de un contraste, y se denota por \( P(θ) \) , como

\(  P(θ)=1-β(θ) \)

donde \(  β(θ) \) es la probabilidad de que un valor del estadístico de contraste no se encuentre en la región crítica cuando \( H_0 \) es falsa. Por lo tanto, \( P(θ) \) representa la probabilidad de que un valor del estadístico de contraste se encuentre dentro de la región crítica cuando \(  H_0 \) es falsa, es decir, es la probabilidad de rechazar la hipótesis \(  H_0 \) cuando ésta es falsa. (Probabilidad que se tiene en el contraste de detectar que \(  H_0 \) es falsa.)

\( P(θ)=1-β(θ)=P[rechazar H_0 / H_0 es falsa]=P[no rechazar H_1 / H_1 es cierta] \)

En la Tabla 10.2 presentamos otra forma de resumir las posibles decisiones y errores junto con la función de potencia

\(  \begin{array}{||l|cc||} \hline &  \hspace{5cm} Decisión   \\ \hline & Rechazar \hspace{.1cm}  H_0 & No \hspace{.1cm}  rechazar H_0 \\ \hline Hipótesis \hspace{.1cm} cierta \hspace{.1cm} H_0 & α & Decisión \hspace{.1cm} correcta \\ \hline Hipótesis \hspace{.1cm} falsa \hspace{.1cm} H_0 & Decisión \hspace{.1cm} correcta \hspace{.2cm} (Potencia) & β \\ \hline \end{array}  \)

Tabla 10.2

Comentario: Recordar que para un \(  α \) fijo, si se incrementa el tamaño de la muestra se disminuye el tamaño del error de tipo II. Por tanto, se deduce que la función de potencia aumentará conforme aumente el tamaño muestral.

P-valor o nivel crítico P o mínimo nivel de significación:

Es el valor de \(  α \) más pequeño que hace que la muestra observada nos indique que se debe rechazar \( H_0 \). Elegido un nivel de significación \(  α \), se rechazará \(  H_0 \)  si p-valor \( < α \).

Contrastes de hipótesis de una población Normal

En esta sección se estudian los contrastes de hipótesis sobre la media y la varianza de una distribución Normal y los contrastes de hipótesis sobre el parámetro p de una distribución Binomial. Se recomienda al lector que consulte la sección 9.2 del Capítulo 9 y haga comparaciones con los intervalos de confianza.

Contrastes de hipótesis para la media de una población Normal

El objetivo es probar uno de los siguientes contrastes de hipótesis con respecto de \( μ \)

\(  \begin{array}{ccccc} H_0 \equiv  \mu = \mu_0 &  &  H_0 \equiv μ \leq μ_0  &  &  H_0 \equiv μ \geq μ_0 \\ & o & & o & \\  H_1 \equiv  μ \neq μ_0  &   &  H_1 \equiv  μ > μ_0  &  &  H_1 \equiv  μ < μ_0 \end{array}  \)

donde \(  μ_0 \) es un valor conocido dado de antemano. Para ello se toma una m.a.s concreta  \( x_1, x_2, \cdots , x_{n} \) cuya media valdrá: \(  \bar {x} = \displaystyle \frac{1} {n} \displaystyle \sum_{i=1}^{n} x_{i} \)

Gráficamente podemos expresar estos contrastes de la siguiente forma:

                             
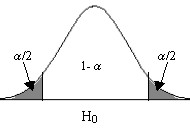
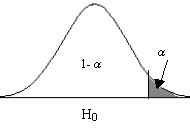
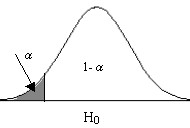
\( \hspace{1.5cm} \) Figura 10.1                                              Figura 10.2                                           Figura 10.3

Distinguiremos dos situaciones: a) Varianza poblacional \( σ^{2} \)  conocida y b) Varianza poblacional \( σ^{2} \)  desconocida.

a) Varianza poblacional \( σ^{2} \) conocida

Sabemos que \( \bar{X} \rightarrow N(μ, σ/ \sqrt{n})  \) y si \( H_0 \equiv μ=μ_0   \) es cierta entonces \(  \bar{X} \rightarrow N(μ_0, σ/ \sqrt {n}) \) por tanto

 \(  Z= \displaystyle \frac {\bar{X}-μ_0} {σ/ \sqrt{n}} \rightarrow N(0, 1) \)

 \(  Z=(\bar{X}-μ_0)/(σ/\sqrt{n})  \) es el estadístico de contraste y dado un nivel de significación α, si \(  H_0  \) es cierta, la mayoría de los valores de la media muestral deben estar próximos al valor \(  μ_0 \)

a1) Para la hipótesis alternativa \(  H_1 \equiv μ \neq μ_0 \), (contraste bilateral también llamado de dos colas), la región de no rechazo es  \( (-z_{α/2}, z_{α/2}) \).

El contraste consiste en tomar una muestra aleatoria y a partir de ella determinar el valor de  \(  Z \)

* Si \(  Z \)  pertenece al intervalo \(  (-z_{α/2}, z_{α/2})  \) no se rechaza \(  H_0 \)

* Si  \(  Z  \) no pertenece al intervalo \(  (-z_{α/2}, z_{α/2})  \) se rechaza \( H_0 \)

o bien, en vez de \(  Z  \) se utiliza \(  |Z|  \) que se suele llamar z experimental y se denota \(  z_{exp} \)

 \(  z_{exp}= \left | \displaystyle \frac {\bar{x}-μ_0} {σ/ \sqrt{n}} \right | \)

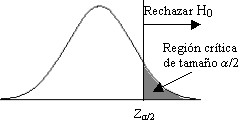
Figura 10.4

Si \(  z_{exp}<z_{α/2} \Rightarrow  \hspace{.2cm}  \) No se rechaza \( \hspace{.2cm}  H_0 \)

Si  \( z_{exp} \geq z_{α/2} \Rightarrow  \hspace{.2cm}  \)  Se rechaza  \( \hspace{.2cm}  H_0 \)

a2) Para la hipótesis alternativa \(  H_1 \equiv μ>μ_0  \) la correspondiente región de no rechazo es \(  (- \infty , z_{α}) \)  y el estadístico de contraste viene dado por

 \(  z_{exp}= \displaystyle \frac {\bar{x}-μ_0} {σ/ \sqrt{n}}  \hspace {1cm}  \)  [10.1]

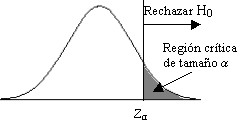
Figura 10.5

Si \(  z_{exp}<z_{α} \Rightarrow  \hspace{.2cm}  \)  No se rechaza \( \hspace{.2cm}  H_0 \)

Si \(  z_{exp} \geq z_{α} \Rightarrow  \hspace{.2cm}  \)  Se rechaza \( \hspace{.2cm}  H_0 \)

a3) Para la hipótesis alternativa \(  H_1 \equiv  μ<μ_0  \) la correspondiente región de no rechazo es \(  (-z_{α} , \infty)  \) y el estadístico de contraste está dado por la expresión [10.1]

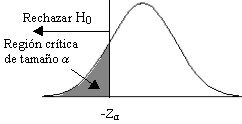
Figura 10.6

Si \(  z_{exp}>-z_{α} \Rightarrow  \hspace{.2cm} \)  No se rechaza \( \hspace{.2cm}  H_0 \)

Si \(  z_{exp} \leq -z_{α} \Rightarrow  \hspace{.2cm} \)  Se rechaza \( \hspace{.2cm}  H_0 \)

La regla de decisión también se puede realizar mediante el P-valor (Área que deja a la derecha el valor experimental del estadístico de contraste).

Elegido un nivel de significación \(  α \) , se rechazará  \( H_0  \) si p-valor < α,

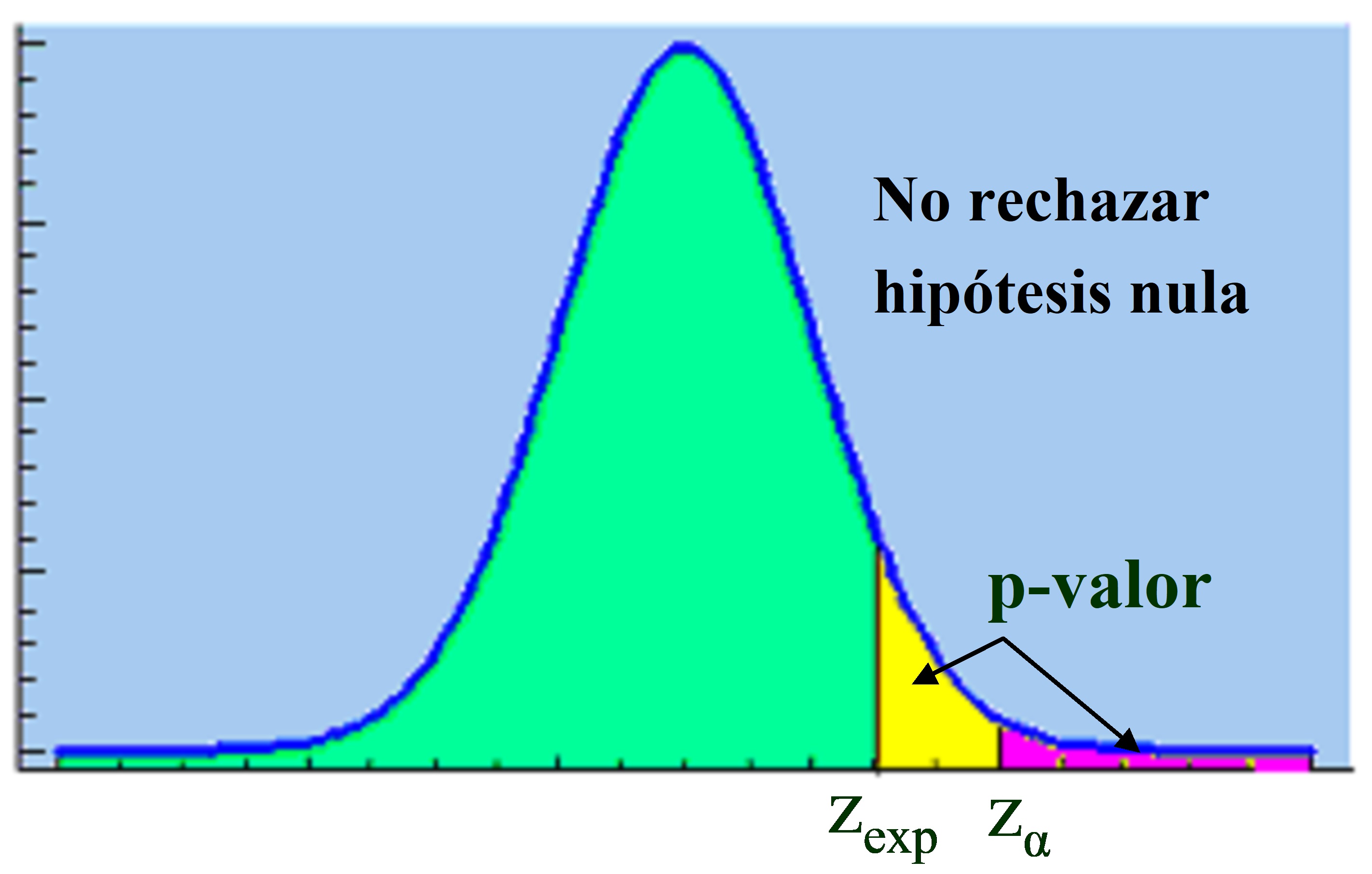
Figura 10.7:  \( α<p-valor \)

∙ Figura 10.7: Si \(  α<p-valor \Rightarrow  \hspace{.2cm} \)  No rechazar \( \hspace{.2cm} H_0 \)

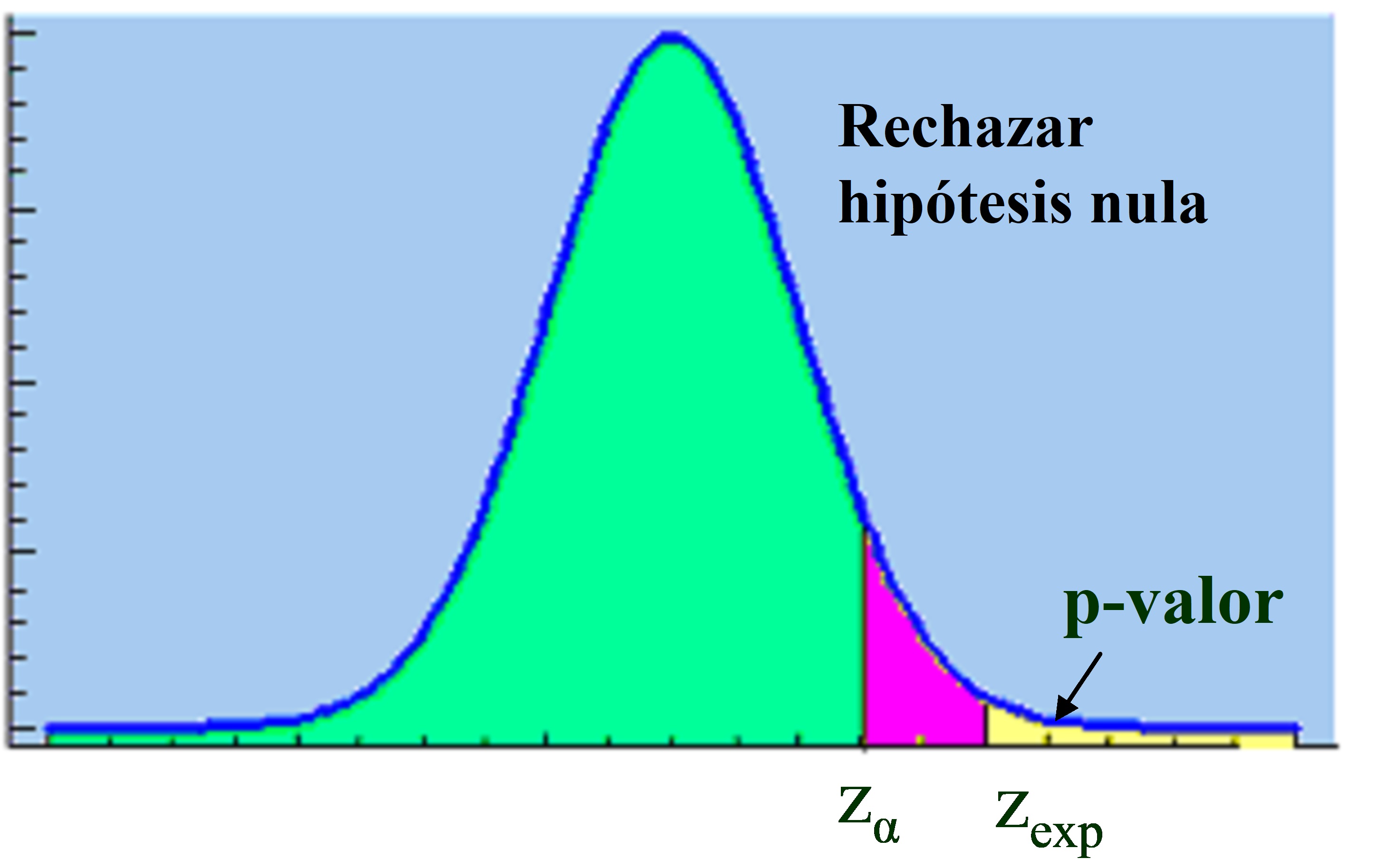
 Figura 10.8: \(  α>p-valor \)

∙ Figura 10.8: Si \(   α>p-valor \Rightarrow  \hspace{.2cm} \) Rechazar \(  \hspace{.2cm} H_0 \)

Ejemplo 10.2. Se quiere comprobar, con un nivel de significación 0.05, si una muestra de tamaño n=20 con media 10 procede de una población que se distribuye según una Normal (14, 3).

Respuesta: Hay que realizar un contraste bilateral para la media poblacional con varianza conocida

\(  \left.  \begin{array} \\  H_0 \equiv  \mu =  14 \\  H_1 \equiv  μ \neq 14 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\ z_{exp} = \left | \displaystyle \frac { \bar {x} -μ_0 } {σ/ \sqrt {n}} \right |= \left | \displaystyle \frac { 10-14} {3/ \sqrt {20}} \right |=5.962 \\ z_{α/2}=z_{0.025}=1.96 < z_{exp} \hspace {.2cm} \Rightarrow Rechazar \hspace {.2cm} H_0 \Rightarrow \\
\hspace {.2cm} La \hspace {.2cm} muestra \hspace {.2cm} no \hspace {.2cm} procede \hspace {.2cm} de \hspace {.2cm} la \hspace {.2cm} citada \hspace {.2cm} población \end{array} \right. \)

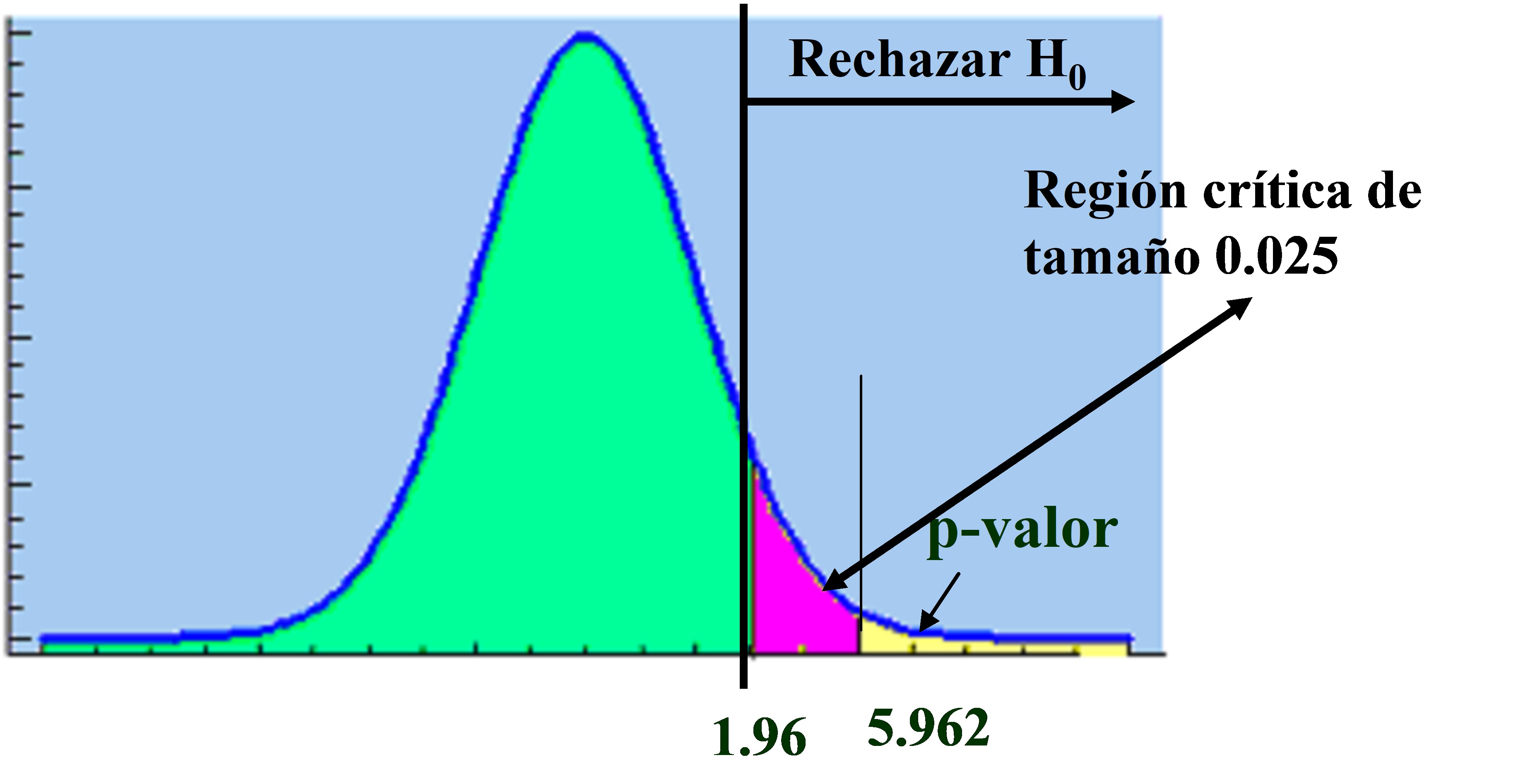Figura 10.9

Ejemplo 10.3. En un preparado alimenticio infantil se especifica que según análisis garantizado el contenido mínimo de proteínas es del 42%. Tratamos de comprobar esta especificación y para ello tomamos 10 preparados que analizamos para determinar su contenido en proteínas, obteniendo una media del 40%. Suponiendo que la variable contenido proteico tiene una distribución Normal con varianza 16. ¿Es correcta la especificación citada para un nivel de significación α=0.05?.

Respuesta: Hay que realizar un contraste unilateral para la media poblacional con varianza conocida

\(  \left.  \begin{array} \\  H_0 \equiv  \mu  \geq 0.42 \\  H_1 \equiv  μ < 0.42 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\ z_{exp} = \left | \displaystyle \frac { \bar {x} -μ_0 } {σ/ \sqrt {n}} \right |= \left | \displaystyle \frac { 0.4 -0.42} {4/ \sqrt {10}} \right |= – 0.0158 \\  -z_{α}= -z_{0.05}= -1.64 < z_{exp} \hspace {.2cm} \Rightarrow No \hspace {.2cm} Rechazar \hspace {.2cm} H_0 \Rightarrow  \\ \hspace {.2cm} Admitimos \hspace {.2cm} como \hspace {.2cm} correcta \hspace {.2cm} la \hspace {.2cm} especificación \hspace {.2cm} del \hspace {.2cm} preparado \end{array} \right. \)

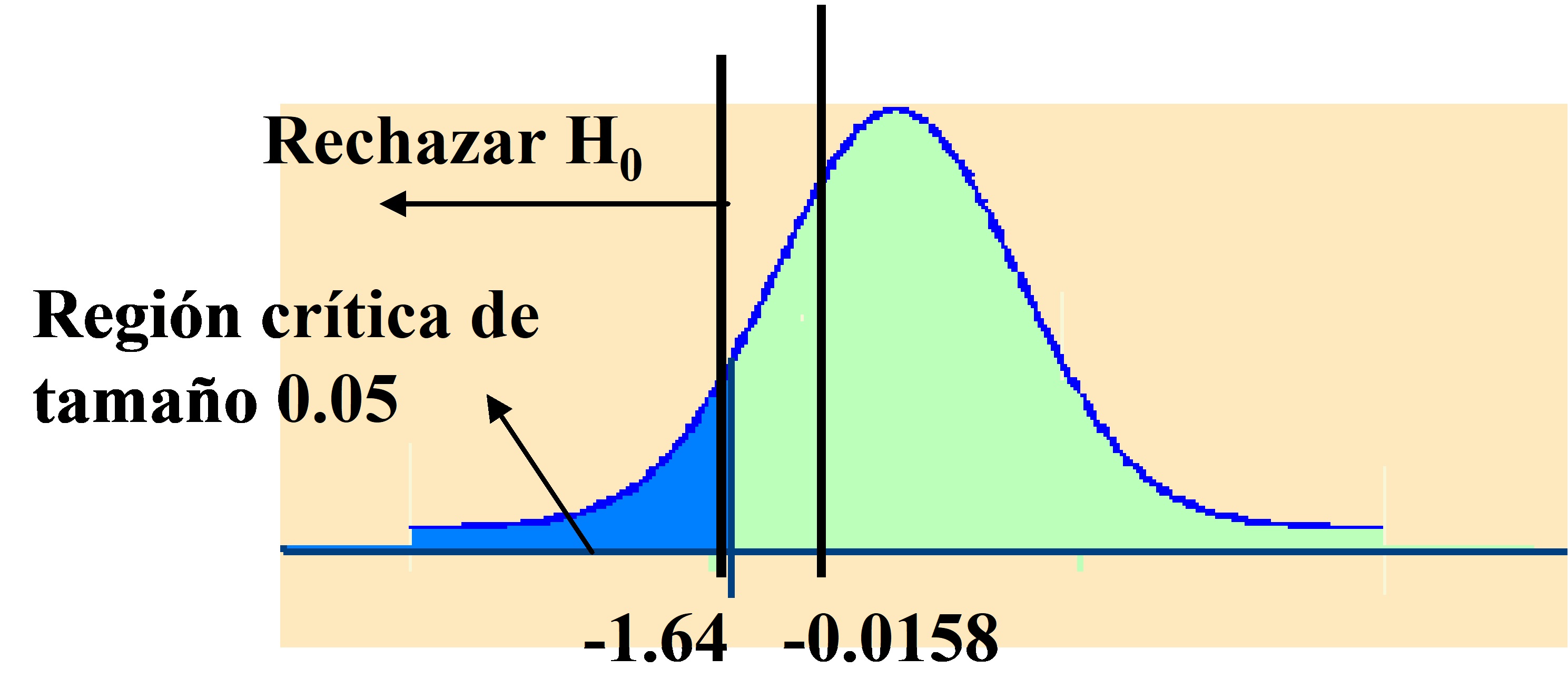Figura 10.10

b) Varianza poblacional \( σ^{2} \) desconocida

En este caso el estadístico de contraste que se utiliza sigue una distribución t-Student y, bajo la hipótesis nula \( H_0 \equiv μ=μ_0 \), dicho estadístico tiene la siguiente expresión

 \(   \displaystyle \frac { \bar {X} -μ_0 } {\widehat {σ} / \sqrt {n-1}}  \rightarrow t_{n-1} \)

Fijado un nivel de significación α

b1) Para la hipótesis alternativa \( H_1 \equiv μ \neq μ_0 \)  la correspondiente región de no rechazo es \(  (-t_{α/2;n-1} , t_{α/2;n-1}) \)  y el estadístico de contraste adopta la forma

\(  t_{exp}= \left | \displaystyle \frac { \bar {x} -μ_0 } {\widehat {σ} / \sqrt {n-1}} \right |= \left | \displaystyle \frac { \bar {x} -μ_0 } {S / \sqrt {n}} \right | \)

y se utiliza la siguiente regla de decisión

\(  \left.  \begin{array} \\  H_0 \equiv  \mu =  \mu_0 \\  H_1 \equiv  μ \neq \mu_0 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\    Si \hspace {.2cm} t_{exp}<t_{α/2;n-1} \Rightarrow \hspace {.2cm} No \hspace {.2cm} se \hspace {.2cm} rechaza \hspace {.2cm} H_0  \\  Si \hspace {.2cm} t_{exp}≥t_{α/2;n-1}\Rightarrow \hspace {.2cm} Se \hspace {.2cm} rechaza \hspace {.2cm}  H_0   \\ \end{array} \right. \)

b2) Para la hipótesis alternativa \( H_1 \equiv μ>μ_0 \) la correspondiente región de no rechazo es \( (-\infty , t_{α;n-1}) \) y el estadístico de contraste tiene la expresión

\(  t_{exp}= \displaystyle \frac { \bar {x} -μ_0 } {\widehat{σ} / \sqrt {n-1}} \hspace{1cm} [10.2] \)

y se adopta la siguiente regla de decisión

\(  \left.  \begin{array} \\  H_0 \equiv  \mu =  \mu_0 \\  H_1 \equiv  μ > \mu_0 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\    Si \hspace {.2cm} t_{exp}<t_{α;n-1} \Rightarrow \hspace {.2cm} No \hspace {.2cm} se \hspace {.2cm} rechaza \hspace {.2cm} H_0  \\  Si \hspace {.2cm} t_{exp}≥t_{α;n-1}\Rightarrow \hspace {.2cm} Se \hspace {.2cm} rechaza \hspace {.2cm}H_0   \\ \end{array} \right. \)

b3) Para la hipótesis alternativa \( H_1 \equiv  μ <  \mu_0  \) la correspondiente región de no rechazo es \(  (-t_{α;n-1}, \infty ) \), el estadístico de contraste es [10.2] y se adopta la siguiente regla de decisión

\(  \left.  \begin{array} \\  H_0 \equiv  \mu =  \mu_0 \\  H_1 \equiv  μ < \mu_0 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\    Si \hspace {.2cm} t_{exp} > – t_{α;n-1} \Rightarrow \hspace {.2cm} No \hspace {.2cm} se \hspace {.2cm} rechaza \hspace {.2cm} H_0  \\  Si \hspace {.2cm} t_{exp} \leq – t_{α;n-1}\Rightarrow \hspace {.2cm} Se \hspace {.2cm} rechaza \hspace {.2cm} H_0   \\ \end{array} \right. \)

Ejemplo 10.4. Se quiere comprobar si 100 observaciones distribuidas normalmente, con desviación típica desconocida, media muestral 10 y cuasidesviación típica 1, pueden proceder de una población Normal N(10.3; σ).

Respuesta: Hay que realizar un contraste bilateral para la media poblacional con varianza desconocida

\(  \left.  \begin{array} \\  H_0 \equiv  \mu =  10.3  \\  H_1 \equiv  μ \neq 10.3 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\ t_{exp} = \left | \displaystyle \frac { \bar {x} -μ_0 } {s/ \sqrt {n}} \right |= \left | \displaystyle \frac { 10-10.3} {1/ \sqrt {100}} \right |=3 \\ t_{α/2; n-1}=t_{0.025;99}=1.984 < t_{exp} \hspace {.2cm} \Rightarrow Rechazar \hspace {.2cm} H_0 \Rightarrow \\  \hspace {.2cm} La \hspace {.2cm} muestra \hspace {.2cm} no \hspace {.2cm} procede \hspace {.2cm} de \hspace {.2cm} la \hspace {.2cm} citada \hspace {.2cm} población \end{array} \right. \)

Ejemplo 10.5. Realizar el Ejemplo 10.3 con varianza poblacional desconocida

Respuesta:

\(  \left.  \begin{array} \\  H_0 \equiv  \mu  \geq 0.42  \\  H_1 \equiv  μ < 0.42  \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\ t_{exp} =  \displaystyle \frac { \bar {x} -μ_0 } {\widehat {σ }/ \sqrt {n-1}} =  \displaystyle \frac { 0.4 – 0.42} {3.5 / \sqrt {9}} = -0.01714  \\  -t_{α; n-1}= -1.833  < t_{exp} \hspace {.2cm} \Rightarrow No \hspace {.2cm} Rechazar \hspace {.2cm} H_0 \Rightarrow \\ \hspace {.2cm} Admitimos \hspace {.2cm} como \hspace {.2cm} correcta \hspace {.2cm} la  \hspace {.2cm}especificación \hspace {.2cm} del \hspace {.2cm} preparado \end{array} \right. \)

Ejemplo 10.6. Una variable estudiada por los biólogos es la temperatura interna del cuerpo en los animales poiquilotermos (animales cuya temperatura corporal fluctúa con el am-biente circundante). El nivel letal (DL50) para los lagartos del desierto es de 45ºC. Se ha observado que la mayor parte de estos animales se oculta del calor en verano para evitar aproximarse a este nivel letal. Se realiza un experimento para estudiar el tiempo (minutos) que se requiere para que la temperatura del cuerpo de un lagarto del desierto alcance los 45ºC partiendo de la temperatura normal de su cuerpo mientras está a la sombra. Se obtuvieron las siguientes observaciones: 10.1 ; 12.5 ; 12.2 ; 10.2 ; 12.8 ; 12.1 ; 11.2 ; 11.4; 10.7 ; 14.9 ; 13.9 ; 13.3. Se pide:

a) Hallar estimaciones puntuales de la media y la varianza
b) Supóngase que la variable X: “Tiempo en alcanzar los 45º” sigue una ley Normal ¿Puede concluirse que el tiempo medio requerido para alcanzar la dosis letal es inferior a 13 minutos?

Respuesta: Dada la v.a. X: “Tiempo en alcanzar los 45º”

a)

\( \widehat {μ} = \bar {x} = \displaystyle \frac { 1} {n}  \displaystyle \sum_{i=1}^{n} x_{i}= \displaystyle \frac {145.3} {12}=12.1083 \)

\( \widehat{σ}^2 = \displaystyle \frac { 1} {n}  \displaystyle \sum_{i=1}^{n} x_{i}^{2}- \bar {x}^2 = \displaystyle \frac { 1} {12} 1783.39-(12.1083) ^{2} =2.004 \hspace{.2cm} ; \hspace{.2cm} \widehat {σ}=1.415 \)

b)

\(  \left.  \begin{array} \\  H_0 \equiv  \mu  \geq 13 \\  H_1 \equiv  μ < 13 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\ t_{exp} = \left | \displaystyle \frac { \bar {x} -μ_0 } {σ/ \sqrt {n – 1}} \right |= \displaystyle \frac { 12.1083 – 13} {1.415/ \sqrt {11}} = – 2.090 \\  -t_{0.05; 11}= -1.796 > t_{exp} \hspace {.2cm} \Rightarrow No \hspace {.2cm} Rechazar \hspace {.2cm} H_0  \end{array} \right. \)

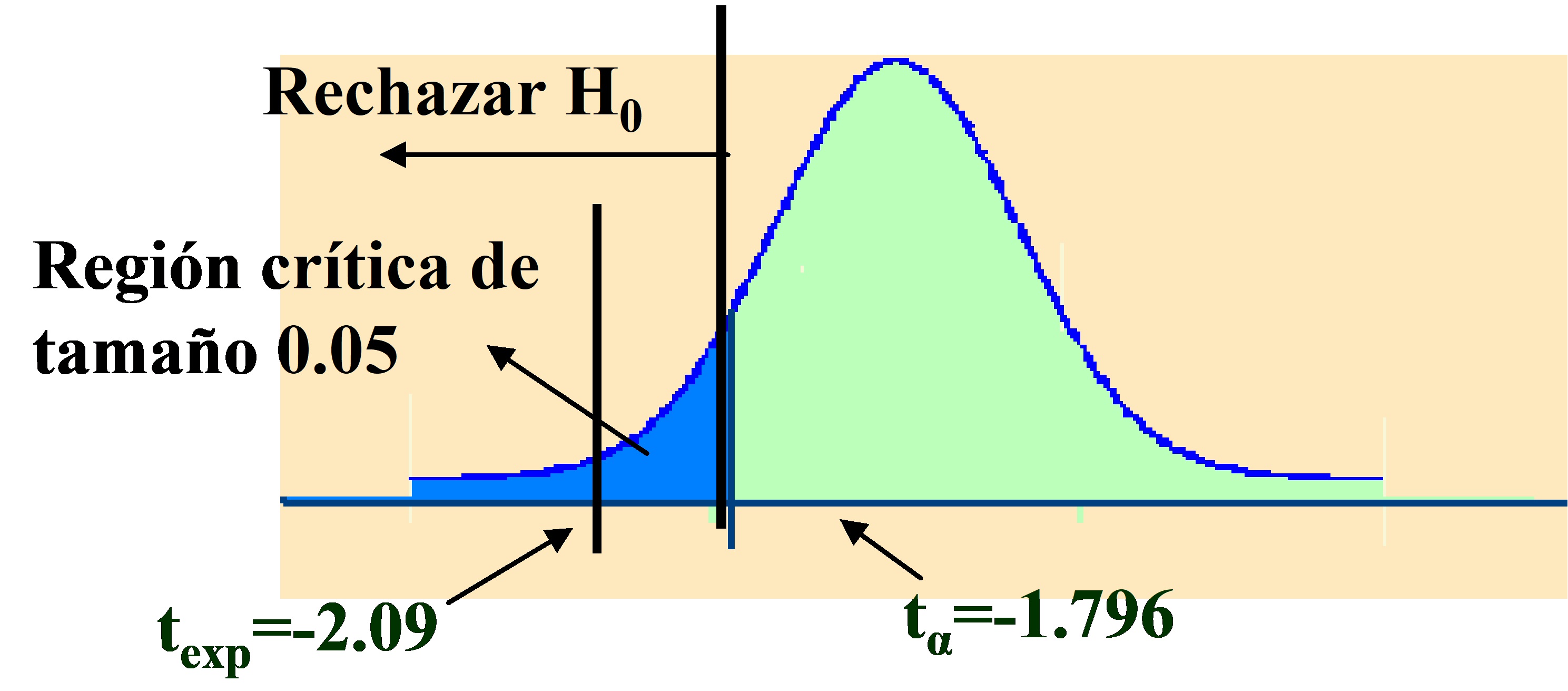
Figura 10.11

Puede concluirse que el tiempo medio para alcanzar la dosis letal es inferior a 13 minutos.

Contrastes de hipótesis para la varianza de una población Normal

Sea \( X_1, X_2, \cdots, X_{n} \) una muestra aleatoria de tamaño n de una distribución Normal con varianza \( σ^2 \) desconocida, siendo \( \bar {X } \) y \( \widehat {σ} \) la media y desviación típica muestral. El objetivo es probar uno de los siguientes contrastes de hipótesis con respecto de \( σ^{2} \):

\(  \begin{array}{ccccc} H_0 \equiv  σ^{2}=σ_{0}^{2}  &  &  H_0 \equiv σ^{2} \leq σ_{0}^{2} &  & H_0 \equiv σ^{2} \geq σ_{0}^{2} \\ & o & & o & \\  H_1 \equiv  σ^{2} \neq σ_{0}^{2} &  &  H_1 \equiv  σ^{2} > σ_{0}^{2} &  &  H_1 \equiv  σ^{2} < σ_{0}^{2} \end{array}  \)

donde \( σ_0^{2} \) es un valor conocido dado de antemano.

El estadístico de contraste adopta distintas formas dependiendo de que la media sea conocida o no.

a) Media poblacional conocida

Sabemos que

\( \displaystyle \frac { \displaystyle \sum_{i=1}^{n} \left ( X_{i}-μ \right )^{2}  } {σ^{2}} \rightarrow  χ_{n}^{2} \)

y si \(  H_0 \equiv  σ^{2}=σ_{0}^{2} \) es cierta entonces

\( \displaystyle \frac { \displaystyle \sum_{i=1}^{n} \left ( X_{i}-μ \right )^{2}} {σ_{0}^{2}} \rightarrow   χ_{n}^{2}  \hspace{1cm} [10.3]\)

Fijado un nivel de significación α, el estadístico de contraste \( χ_{exp}^{2} \), bajo la hipótesis nula \( H_0 \equiv  σ^{2}=σ_{0}^{2} \), sigue una distribución \( χ_{n}^{2} \) y tiene la expresión dada en ([10.3])

\(  \begin{array}{| l| l |} \hline Hipótesis \hspace{ .2cm} alternativa & Regla \hspace{ .2cm} de \hspace{ .2cm} decisión \\ \hline
H_1 \equiv σ^{2} \neq σ_{0}^{2} & Rechazar \hspace{ .2cm} H_0  \hspace{ .2cm}cuando \hspace{ .2cm} χ_{exp}^{2} \geq  χ_{α/2;n}^{2} \hspace{ .2cm} o \hspace{ .2cm} χ_{exp}^{2} \leq χ_{1-α/2;n}^{2} \\ \hline H_1 \equiv σ^{2} > σ_{0}^{2}  & Rechazar \hspace{ .2cm} H_0 \hspace{ .2cm} cuando \hspace{ .2cm} χ_{exp}^{2} \geq χ_{α;n}^{2} \\  \hline H_1 \equiv σ^{2} < σ_{0}^{2} & Rechazar  \hspace{ .2cm} H_0 \hspace{ .2cm} cuando  \hspace{ .2cm} χ_{exp}^{2} \leq χ_{1-α;n}^{2} \\ \hline \end{array}  \)

b) Media poblacional desconocida

Sabemos que

\(  \displaystyle \frac { \displaystyle \sum_{i=1}^{n} \left ( X_{i}-\bar {X} \right )^{2}  } {σ^{2}} =  \displaystyle \frac { (n-1)S^{2}}{σ^{2}} \rightarrow  χ_{n-1}^{2} \)

y si \( H_0 \equiv σ^{2}= σ_{0}^{2} \) es cierta entonces

\(  \displaystyle \frac { \displaystyle \sum_{i=1}^{n} \left ( X_{i}-\bar {X} \right )^{2}  } {σ_{0}^{2}} =  \displaystyle \frac { (n-1)S^{2}}{σ_{0}^{2}} \rightarrow  χ_{n-1}^{2} \hspace{2cm} [10.4] \)

Fijado un nivel de significación α, el estadístico de contraste \( χ_{exp}^{2} \), bajo la hipótesis nula \( H_0 \equiv σ^{2}= σ_{0}^{2} \), sigue una distribución \( χ_{n-1}^{2} \) y tiene la expresión dada en ([10.4])

Se adopta la misma regla de decisión que el caso anterior pero teniendo en cuenta que, en esta situación, la distribución Chi-cuadrada tiene n-1 grados de libertad.

Ejemplo 10.7. Se quiere comprobar si en un determinado experimento la varianza es 4, para ello se toma una muestra aleatoria de tamaño 28 de una población Normal con media desconocida y varianza muestral 2.

Respuestas: Hay que realizar un contraste bilateral para la varianza poblacional con media desconocida

\(  \left.  \begin{array} \\  H_0 \equiv  σ^{2}=4 \\  H_1 \equiv  σ^{2}\neq 4 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\ χ_{exp}^{2} = \displaystyle \frac { n \widehat{σ}^{2} } {σ_{0}^{2}}= \displaystyle \frac { 28 \times 2} {4} = 14 \\  χ_{α/2;n-1}^{2} =  χ_{0.025;27}^{2}= 43.2 > χ_{exp}^{2} \\   χ_{1-α/2;n-1}^{2} =χ_{0.975;27}^{2} =14.6 > χ_{exp}^{2}  \Rightarrow Se  \hspace {.2cm} Rechaza \hspace {.2cm} H_0  \end{array} \right. \)

 

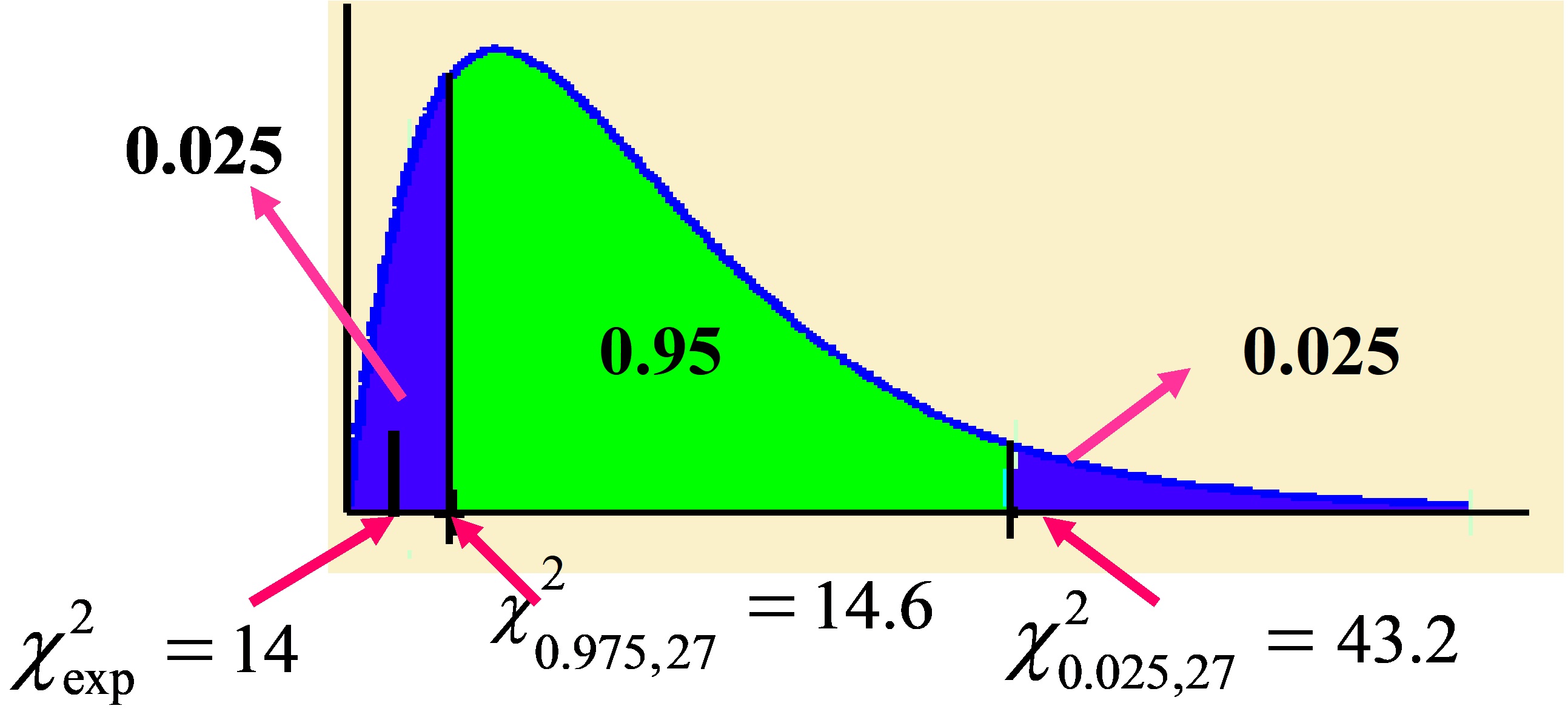
Figura 10.12

Ejemplo 10.8: Con los datos del Ejemplo 10.6 contestar a la siguiente pregunta: ¿Puede concluirse que la desviación típica de X sea inferior a 1.5 minutos?

Respuesta:

\(  \left.  \begin{array} \\  H_0 \equiv  σ^{2} \geq  1.5^{2} \\  H_1 \equiv  σ^{2} < 1.5^{2} \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\ χ_{exp}^{2} = \displaystyle \frac { n \widehat{σ}^{2} } {σ_{0}^{2}}= \displaystyle \frac { 12 \times 2.004} {1.5^{2}} = 10.688  \\  χ_{1 – α;n-1}^{2} =  χ_{0.95;11}^{2}= 4.57 \\   χ_{exp}^{2} > χ_{1 – α;n-1}^{2} =4.57  \Rightarrow No \hspace {.2cm} Rechazar \hspace {.2cm} H_0  \end{array} \right. \)

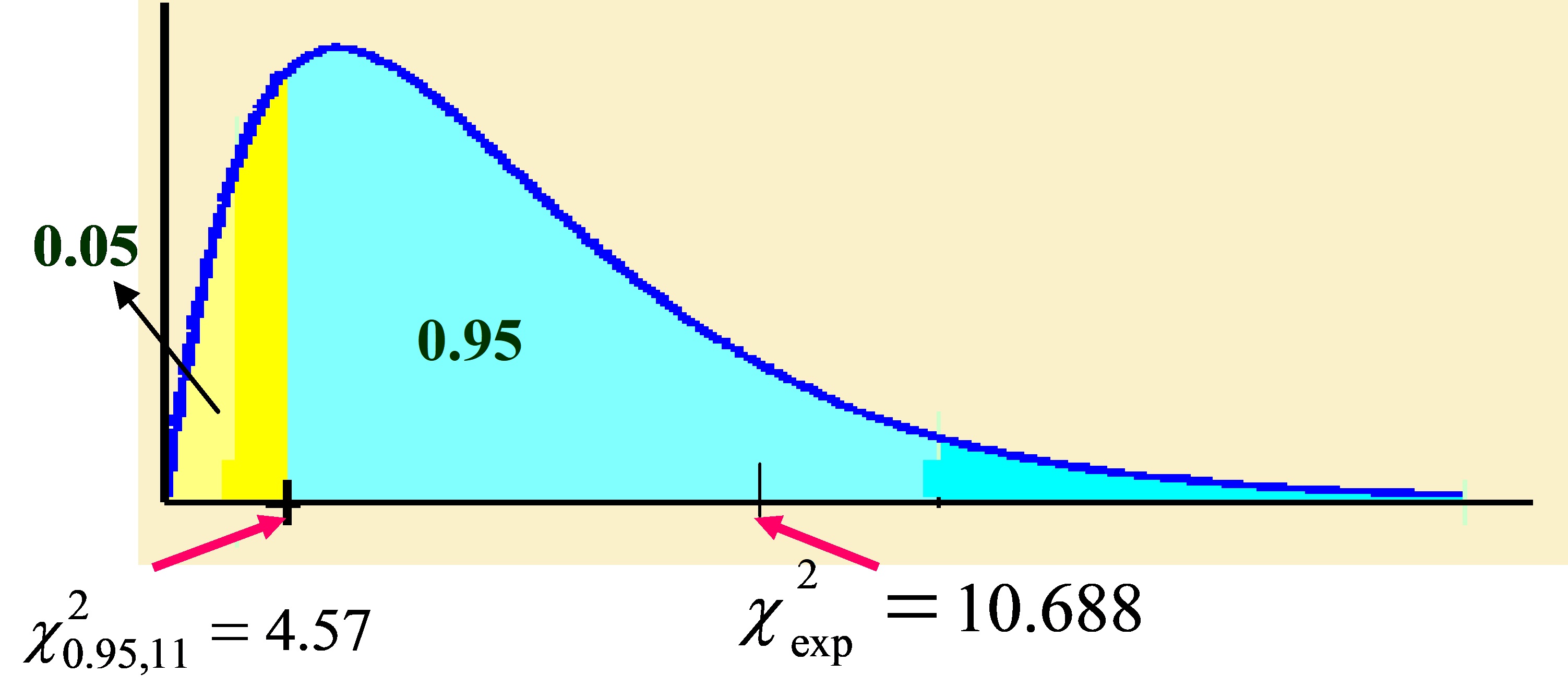
Figura 10.13

No puede concluirse que la desviación típica de X sea inferior a 1.5 minutos.

Contrastes para el parámetro p de una distribución Binomial

Si se toma una muestra aleatoria de tamaño n, suficientemente grande y denotamos por \( p \) y \( \widehat{p} \) las proporciones de éxitos de la población y de dicha muestra, respectivamente se verifica que

\( \widehat{p}  \rightarrow  N \left ( p,  \displaystyle \sqrt{\displaystyle \frac {\widehat{p} \widehat{q}}{n} } \right ) \hspace{2cm} o \hspace{2cm}  \displaystyle \frac{  \widehat{p}-p}{  \displaystyle \sqrt{\displaystyle \frac {\widehat{p} \widehat{q}}{n} }  } \rightarrow  N(0, 1) \)

Fijado un nivel de significación α

a) Para la hipótesis alternativa \( H_1 \equiv p \neq p_0 \) la correspondiente región de no rechazo es \( (-z_{α/2} , z_{α/2}) \) y el estadístico de contraste, bajo la hipótesis nula \( H_0 \equiv p=p_0 \), adopta la siguiente expresión:

\( z_{exp}=  \displaystyle \frac { \left | \widehat{p} -p_0 \right | }{\displaystyle \sqrt{\displaystyle \frac {\widehat{p} \widehat{q}}{n} } } \)

Se utiliza la siguiente regla de decisión

\(  \left.  \begin{array} \\  H_0 \equiv  p = p_0 \\  H_1 \equiv p \neq p_0 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\ Si \hspace {.2cm}  Z_{exp} < z_ {α/2} \Rightarrow  No \hspace {.2cm} se \hspace {.2cm} Rechaza \hspace {.2cm} H_0   \\  Si \hspace {.2cm} Z_{exp}  \geq z_ {α/2} \Rightarrow  Se \hspace {.2cm} Rechaza \hspace {.2cm} H_0 \end{array} \right. \)

b) Para la hipótesis alternativa \( H_1 \equiv p > p_0 \) la correspondiente región de no rechazo es \( (-∞ , z_{α}) \) y el estadístico de contraste está dado por

\( z_{exp}=\displaystyle \frac{  \widehat{p}-p}{  \displaystyle \sqrt{\displaystyle \frac {\widehat{p} \widehat{q}}{n} }  }  \hspace{2cm} [ 10.5 ]  \)

y se adopta la siguiente regla de decisión

\(  \left.  \begin{array} \\  H_0 \equiv  p = p_0 \\  H_1 \equiv p > p_0 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\ Si \hspace {.2cm}  Z_{exp} < z_ {α} \Rightarrow  No \hspace {.2cm} se \hspace {.2cm} Rechaza \hspace {.2cm} H_0   \\  Si \hspace {.2cm} Z_{exp}  \geq z_ {α} \Rightarrow  Se \hspace {.2cm} Rechaza \hspace {.2cm} H_0 \end{array} \right. \)

c) Para la hipótesis alternativa \( H_1 \equiv p < p_0 \)  la correspondiente región de no rechazo es \(  (-z_{α} , ∞) \), el estadístico de contraste es ([10.5]) y se adopta la siguiente regla de decisión

\(  \left.  \begin{array} \\  H_0 \equiv  p = p_0 \\  H_1 \equiv p < p_0 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\ Si \hspace {.2cm}  Z_{exp} > – z_ {α} \Rightarrow  No \hspace {.2cm} se \hspace {.2cm} Rechaza \hspace {.2cm} H_0   \\  Si \hspace {.2cm} Z_{exp}  \leq – z_ {α} \Rightarrow  Se \hspace {.2cm} Rechaza \hspace {.2cm} H_0 \end{array} \right. \)

Ejemplo 10.9. Se ignora la proporción de familias numerosas y con el fin de determinar dicha proporción se toma una muestra de 800 familias siendo la proporción observada de 0.18. Formulamos las siguientes hipótesis: H₀:p=0.20 frente a la alternativa H₁=p≠0.20 que queremos contrastar para un nivel de significación α=0.05.

Respuesta:

\(  \left.  \begin{array} \\  H_0 \equiv  p = 0.20  \\  H_1 \equiv  p \neq 0.20 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\ z_{exp}=\displaystyle \frac{ \left | \widehat{p}-p_0 \right |}{  \displaystyle \sqrt{\displaystyle \frac {\widehat{p} \widehat{q}}{n} }  }  =  \displaystyle \frac {\left | 0.18 – 0.20 \right |}{ \displaystyle \sqrt { \displaystyle \frac { 0.18 \times 0.82 }{800} } } = 1.472  \\  z_{α/2} = z_{0.025} = 1.96 > z_{exp}  \Rightarrow No \hspace {.2cm}Se \hspace {.2cm} Rechaza \hspace {.2cm} H_0  \end{array} \right. \)

Por lo tanto la proporción de familias numerosas se toma igual a 0.20.

Contrastes de hipótesis en dos poblaciones normales: Muestras independientes y muestras apareadas

En las sesiones siguientes los contrastes de hipótesis se efectuarán bajo dos tipos de muestreo: muestras independientes y muestra apareadas.

Recordemos que dos muestras se dicen que son independientes cuando las observaciones de una de ellas no condicionan a las observaciones de la otra y dos muestras se dicen apareadas cuando cada dato de una muestra tiene su homónimo en la otra con el que está relacionado, cada observación de una muestra está emparejada con una observación de la otra muestra. Ejemplos de esta clase de emparejamiento ocurren en estudios en los que se suministran dos tratamientos al mismo sujeto, en estudios con contrastes a priori y a posteriori etc.

Para aclarar estos dos conceptos supongamos que se realiza un estudio para investigar el efecto de un medicamento en individuos diabéticos. El experimento se podría planificar de dos formas:

• Se eligen 20 individuos diabéticos al azar y se les suministra el medicamento a 10 de ellos dejando sin suministrar el medicamento a los otros 10. Transcurrido un tiempo se miden los niveles de glucosa en los dos grupos y se comprueba si el medicamento ha tenido efecto, para ello se contrasta la hipótesis \( H_0 \equiv  μ_1=μ_2 \) para comprobar si las medias son iguales o no. En este caso, las dos muestras están formadas por individuos distintos sin relación entre sí, son muestras independientes.
• Se eligen 20 individuos diabéticos al azar a los que se les suministra el medicamento y se anotan los niveles de glucosa antes y después de aplicar el medicamento y se contrasta la hipótesis \( H_0 \equiv  μ_1=μ_2 \) para responder a la pregunta sobre la efectividad del medicamento. En este caso los datos vienen por pareja (niveles de glucosa antes y niveles de glucosa después), las muestras están relacionadas. Son muestras apareadas.

Contrastes de hipótesis en dos poblaciones normales independientes

En esta sección se estudian los contrastes de hipótesis sobre las medias, varianzas y proporciones de dos poblaciones independientes.

Supongamos que \( X \) e \( Y \) son dos variables aleatorias independientes y tales que   \( X \rightarrow N(μ_{X}, σ_{X}) \) e  \( Y \rightarrow N(μ_{Y}, σ_{Y}) \) .

• Sea \( ( X_1, X_2, \cdots, X_{n_{X}}) \) una m.a.s. de tamaño \( n_{X} \) extraída de la población \(  N(μ_{X}, σ_{X}) \) y denotamos por \( \bar{X} \) y \( \widehat{σ}_{X}^{2} \), a la media muestral y a la varianza muestral, respectivamente.
• Sea \( ( Y_1, Y_2, \cdots, Y_{n_{Y}}) \) una m.a.s. de tamaño \( n_{Y} \) extraída de la población \(  N(μ_{Y}, σ_{Y}) \) y denotamos por \( \bar{Y} \) y \( \widehat{σ}_{Y}^{2} \), a la media muestral y a la varianza muestral, respectivamente.

Contrastes de comparación de dos medias

Consideramos dos poblaciones normales \(  N(μ_{X}, σ_{X}) \) y \(  N(μ_{Y}, σ_{Y}) \) cuyas medias \( μ_{X} \) y \(  μ_{Y} \) se desconocen. El objetivo es probar uno de los siguientes contrastes de hipótesis:

\(  \begin{array}{ccccc} H_0 \equiv  μ_{X}-μ_{Y}=μ_0 &  &  H_0 \equiv μ_{X}-μ_{Y} \leq μ_0 &  &  H_0 \equiv μ_{X}-μ_{Y} \geq μ_0 \\ & o & & o & \\  H_1 \equiv  μ_{X}-μ_{Y} \neq μ_0  &  &  H_1 \equiv μ_{X}-μ_{Y} > μ_0  &  &  H_1 \equiv  μ_{X}-μ_{Y} < μ_0 \end{array}  \)

conocidas las medias muestrales \( \bar {x} \) e  \( \bar {y} \)  y los tamaños \( n_{X} \) y \( n_{Y} \) de las muestras. Para ello distinguiremos las siguientes situaciones:

a) Varianzas poblaciones conocidas

Sabemos que \( \overline {X} – \overline {Y} \rightarrow \left ( μ_{X}-μ_{Y},  \displaystyle \sqrt { \displaystyle \frac {σ_{X}^{2}} {n_{X }} + \displaystyle \frac{σ_{Y}^{2}}{n_{Y} } } \right ) \)  y si \(  H_0 \) es cierta ( \( H_0 \equiv  μ_{X}-μ_{Y}=μ_0 \) ) entonces \( \overline {X} – \overline {Y} \rightarrow \left ( μ_{0},  \displaystyle \sqrt { \displaystyle \frac {σ_{X}^{2}} {n_{X }} + \displaystyle \frac {σ_{Y}^{2}}{n_{Y} } } \right) \) por tanto

\( Z= \displaystyle \frac{ ( \overline {X} – \overline {Y})- μ_0} { \displaystyle \sqrt { \displaystyle \frac {σ_{X}^{2}} {n_{X }} + \displaystyle \frac{σ_{Y}^{2}}{n_{Y} } } }  \rightarrow  N(0, 1) \)

\( Z=(( \overline {X} – \overline {Y})- μ_0 )/ \displaystyle \sqrt { (σ_{X}^{2} /n_{X})+(σ_{Y}^{2}/n_{Y})} \) es el estadístico de contraste y dado un nivel de significación α:

a1) Para la hipótesis alternativa \( H_1 \equiv μ_{X}-μ_{Y} \neq μ_0 \) la correspondiente región de no rechazo es \( (-z_{α/2} , z_{α/2}) \) y el estadístico de contraste, bajo la hipótesis nula \( H_0 \equiv μ_{X}-μ_{Y}=μ_0 \), tiene la siguiente expresión:

\( z_{exp}= \displaystyle \frac{ \left | ( \overline {x} – \overline {y})- μ_0 \right | } { \displaystyle \sqrt { \displaystyle \frac {σ_{x}^{2}} {n_{x }} + \displaystyle \frac{σ_{y}^{2}}{n_{y} } } }  \)

Se adopta la siguiente regla de decisión:

 \(  \left.  \begin{array} \\  H_0 \equiv  μ_{X}-μ_{Y}=μ_0 \\  H_1 \equiv μ_{X}-μ_{Y} \neq μ_0 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\    Si \hspace {.2cm} z_{exp}<z_{α/2} \Rightarrow \hspace {.2cm} No \hspace {.2cm} se \hspace {.2cm} rechaza \hspace {.2cm} H_0  \\  Si \hspace {.2cm} z_{exp} \geq z_{α/2}\Rightarrow \hspace {.2cm} Se \hspace {.2cm} rechaza \hspace {.2cm}  H_0   \\ \end{array} \right. \)

a2) Para la hipótesis alternativa \( H_1 \equiv μ_{X}-μ_{Y} > μ_0 \) la correspondiente región de no rechazo es \(  (-∞ , z_{α}) \) y el estadístico de contraste viene dado por

\( z_{exp}= \displaystyle \frac{  ( \overline {x} – \overline {y})- μ_0  } { \displaystyle \sqrt { \displaystyle \frac {σ_{x}^{2}} {n_{x }} + \displaystyle \frac{σ_{y}^{2}}{n_{y} } } }  \hspace{2 cm } [10.6]  \)

y se adopta la siguiente regla de decisión

 \(  \left.  \begin{array} \\  H_0 \equiv  μ_{X}-μ_{Y} \leq μ_0 \\  H_1 \equiv μ_{X}-μ_{Y} > μ_0 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\    Si \hspace {.2cm} z_{exp}<z_{α} \Rightarrow \hspace {.2cm} No \hspace {.2cm} se \hspace {.2cm} rechaza \hspace {.2cm} H_0  \\  Si \hspace {.2cm} z_{exp} \geq z_{α}\Rightarrow \hspace {.2cm} Se \hspace {.2cm} rechaza \hspace {.2cm}  H_0   \\ \end{array} \right. \)

a3) Para la hipótesis alternativa \( H_1 \equiv μ_{X}-μ_{Y} < μ_0 \) la correspondiente región de no rechazo es \( (-z_{α} , ∞) \), el estadístico de contraste es ([10.6]) y se adopta la siguiente regla de decisión

 \(  \left.  \begin{array} \\  H_0 \equiv  μ_{X}-μ_{Y} \geq μ_0 \\  H_1 \equiv μ_{X}-μ_{Y} < μ_0 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\    Si \hspace {.2cm} z_{exp}> -z_{α} \Rightarrow \hspace {.2cm} No \hspace {.2cm} se \hspace {.2cm} rechaza \hspace {.2cm} H_0  \\  Si \hspace {.2cm} z_{exp} \leq – z_{α}\Rightarrow \hspace {.2cm} Se \hspace {.2cm} rechaza \hspace {.2cm}  H_0   \\ \end{array} \right. \)

Ejemplo 10.10. Se quieren comparar dos poblaciones de rana pipiens aisladas geográficamente. Para ello se toman dos muestras de ambas poblaciones de tamaños 20 y 25 y se les mide la longitud del cuerpo expresado en milímetros, obteniéndose como resultado un valor medio de 50 y 60 unidades de medidas, respectivamente. Por estudios realizados anteriormente se sabe que las varianzas poblaciones valen 220 y 160 para cada una de las poblaciones. Contrastar la hipótesis de igualdad de medias con un nivel de significación del 5% (Suponiendo que la longitud se distribuya según una Normal).

Respuesta:

\( X  \): “Longitud del cuerpo de ranas1”;  \(  X \rightarrow N(μ_{X}, σ_{X})  \)

\( Y  \): “Longitud del cuerpo de ranas2” ;  \(  Y \rightarrow N(μ_{Y}, σ_{Y})  \)

\(  \left.  \begin{array} \\  H_0 \equiv  μ_{X}-μ_{Y} = μ_0 = 0 \Rightarrow H_0 \equiv  μ_{X} = μ_{Y}  \\  H_1 \equiv μ_{X}-μ_{Y} \neq μ_0 = 0  \Rightarrow H_1 \equiv  μ_{X} \neq μ_{Y}    \\ \end{array} \right \} \rightarrow \)

 \(  \left \{  \begin{array} \\    z_{exp}=  \displaystyle \frac{ \left | \overline {x} – \overline {y} \right | } { \displaystyle \sqrt { \displaystyle \frac {σ_{x}^{2}} {n_{x }  } + \displaystyle \frac{σ_{y}^{2}}{n_{y}}  }  }    =   \displaystyle \frac{ \left | 50 – 60 \right | } { \displaystyle \sqrt { \displaystyle \frac {220} {20 } + \displaystyle \frac{160}{25}  }     } = 2.397  \\    z_{α/2} = z_{0.025} = 1.96 < z_{exp} \Rightarrow \hspace {.2cm} Se \hspace {.2cm} rechaza \hspace {.2cm}  H_0   \\ \end{array} \right. \)

b) Varianzas poblacionales desconocidas

El estadístico de contraste adopta distintas formas dependiendo de que las varianzas sean iguales o distintas

b1) Varianzas poblaciones desconocidas pero supuestas iguales y no se pueden estimar por ser los tamaños muestrales pequeños

En este caso el estadístico de contraste que se utiliza tiene una distribución t-Student y bajo la hipótesis nula  \( H_0 \equiv  μ_{X}-μ_{Y} = μ_0   \) dicho estadístico tiene la siguiente expresión

\( T= \displaystyle \frac{ ( \overline {X} – \overline {Y}) – μ_0}{   \displaystyle \sqrt { \displaystyle \frac {(n_{X}-1)S_{X}^{2}+ (n_{Y}-1) S_{Y}^{2}} {n_{X } – x_{Y} – 2 }  } \displaystyle \sqrt {  \displaystyle \frac{1}{n_{X}} +  \displaystyle \frac{1}{n_{Y}}}  }\rightarrow  t_{n_{X} + n_{Y}-2} \)

Fijado un nivel de significación α, la correspondiente región de no rechazo para el contraste bilateral es \( (-t_{α/2;n_{X}+n_{Y}-2}, t_{α/2;n_{X}+n_{Y}-2}) \) y el estadístico de contraste adopta la forma:

\( t_{exp}= \displaystyle \frac{ \left | ( \overline {x} – \overline {y}) – μ_0 \right |}{   \displaystyle \sqrt { \displaystyle \frac {(n_{X}-1)s_{X}^{2}+ (n_{Y}-1) s_{Y}^{2}} {n_{X } – x_{Y} – 2 }  } \displaystyle \sqrt {  \displaystyle \frac{1}{n_{X}} +  \displaystyle \frac{1}{n_{Y}}}  } \)

y la regla de decisión es

\(  \left.  \begin{array} \\  H_0 \equiv  μ_{X}-μ_{Y}=μ_0 \\  H_1 \equiv μ_{X}-μ_{Y} \neq μ_0 \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\    Si \hspace {.2cm} t_{exp}<t_{α/2; n_{X}+n_{Y}-2 } \Rightarrow \hspace {.2cm} No \hspace {.2cm} se \hspace {.2cm} rechaza \hspace {.2cm} H_0  \\  Si \hspace {.2cm} t_{exp} \geq t_{α/2;n_{X}+n_{Y}-2} \Rightarrow \hspace {.2cm} Se \hspace {.2cm} rechaza \hspace {.2cm}  H_0   \\ \end{array} \right. \)

Nota: En el resto de la sección sólo realizamos los contrastes bilaterales. De los estudios anteriores los contrastes unilaterales deben ser evidentes.

Ejemplo 10.11. Se sabe que la duración de una determinada enfermedad sigue la ley Normal. Para la curación de dicha enfermedad se aplica un determinado antibiótico. Se desea comparar la duración de la enfermedad según que al enfermo se le haya aplicado o no, en otra ocasión dicho antibiótico. Observamos 6 enfermos a los que no se había aplicado anteriormente el antibiótico y la duración media de la enfermedad ha sido de 12 días y 5 enfermos a los que sí se había aplicado, obteniendo una duración de la enfermedad de 15 días. La estimación de la varianza es 16. ¿Qué podemos afirmar acerca de la duración de la enfermedad para α=0.01.

Respuesta:

\(  \left.  \begin{array} \\  H_0 \equiv  μ_{X} = μ_{Y}   \\  H_1 \equiv  μ_{X} \neq μ_{Y}    \\ \end{array} \right \} \rightarrow   \left \{  \begin{array} \\    t_{exp}=  \displaystyle \frac{ \left | \overline {x} – \overline {y} \right | } { s_{p} \displaystyle \sqrt { \displaystyle \frac {1} {n_{x }  } + \displaystyle \frac{ 1}{n_{y}}    }    }    =   \displaystyle \frac{ \left | 12 – 15 \right | } { 4 \displaystyle \sqrt { \displaystyle \frac {1} {6 } + \displaystyle \frac{1}{5}    }       } = 1.239  \\    t_{α/2;n_{x}+n_{y}-2} = t_{0.005;9} = 3.250  >  t_{exp} \Rightarrow \hspace {.2cm} No \hspace {.2cm} se \hspace {.2cm} rechaza \hspace {.2cm}  H_0   \\ \end{array} \right. \)

La duración media de la enfermedad es la misma para los enfermos a los que se les ha aplicado anteriormente el antibiótico y para los que no se les ha aplicado.

b2) Varianzas poblaciones desconocidas pero se pueden estimar por ser los tamaños muestrales grandes

En este caso el estadístico de contraste que se utiliza tiene una distribución Normal y bajo la hipótesis nula \( H_0 \equiv  μ_{X}-μ_{Y}=μ_0 \) dicho estadístico tiene la siguiente expresión

\( Z= \displaystyle \frac{ ( \overline {X} – \overline {Y}) – μ_0}{   \displaystyle \sqrt { \displaystyle \frac {S_{X}^{2}} {n_{X} } +  \displaystyle \frac {S_{Y}^{2}} {n_{Y} } }  } \rightarrow  N(0,1) \)

Fijado un nivel de significación α, la región de no rechazo para el contraste bilateral es \(  (-z_{α/2}, z_{α/2}) \) y el estadístico de contraste adopta la forma:

\( z_{exp}= \displaystyle \frac{ \left | ( \overline {x} – \overline {y}) – μ_0 \right |}{   \displaystyle \sqrt { \displaystyle \frac {s_{X}^{2}} {n_{x} } +  \displaystyle \frac {s_{y}^{2}} {n_{y} } }   } \)

y la regla de decisión es:

\(    \left \{  \begin{array} \\    Si \hspace {.2cm} z_{exp}< z_{α/2 } \Rightarrow \hspace {.2cm} No \hspace {.2cm} se \hspace {.2cm} rechaza \hspace {.2cm} H_0  \\  Si \hspace {.2cm} z_{exp} \geq z_{α/2} \Rightarrow \hspace {.2cm} Se \hspace {.2cm} rechaza \hspace {.2cm}  H_0   \\ \end{array} \right. \)

Ejemplo 10.12. A los 100 alumnos de una clase se les separa en dos grupos, aquellos que practican habitualmente un deporte y los que no practican ninguno, formado cada grupo por 60 y 40 alumnos respectivamente. Les medimos la altura y obtenemos para el primer grupo una media de 1.80 m. y desviación típica de 0.08 m. y para el segundo grupo una media de 1.76 m. y una desviación típica de 0.10 m. ¿Se puede afirmar con un nivel de confianza del 95% que los alumnos que practican algún deporte son más altos? Supóngase que la altura se distribuye normalmente.

Respuesta: Hay que realizar un contraste unilateral para la igualdad de medias con varianzas desconocidas y muestras grandes

\(  \left.  \begin{array} \\  H_0 \equiv  μ_{1} \leq μ_{2}   \\  H_1 \equiv  μ_{1} > μ_{2}    \\ \end{array} \right \} \rightarrow   \left \{  \begin{array} \\    z_{exp}=  \displaystyle \frac{  \overline {x}_1 – \overline {y}_2 } {  \displaystyle \sqrt { \displaystyle \frac {s_{1}^{2}} {n_{1 }  } + \displaystyle \frac{ s_{2}^{2}}{n_{2}}    }    }    =   \displaystyle \frac{1.80 -1.76 } { \displaystyle \sqrt { \displaystyle \frac {0.08^{2}} {60 } + \displaystyle \frac{0.10^{2}}{40}    }       } = 2.118  \\    z_{α} = z_{0.05} = 1.64 <  z_{exp} \Rightarrow Se \hspace {.2cm} rechaza \hspace {.2cm}  H_0 \Rightarrow \\ Los \hspace {.2cm} alumnos \hspace {.2cm}
que \hspace {.2cm}  practican \hspace {.2cm} algún \hspace {.2cm} deporte \hspace {.2cm} son \hspace {.2cm} más \hspace {.2cm} altos  \\ \end{array} \right. \)

Contrastes de comparación de dos proporciones

Si se se toman dos muestras aleatorias de tamaños \( n_{X} \) y \( n_{Y} \), suficientemente grandes y denotamos por \(  p_{X}, p_{Y}, \widehat {p}_{X}, \widehat{ p}_{Y} \) las proporciones de éxitos de cada una de las poblaciones y de dichas muestras, respectivamente se verifica que

\( \widehat {p}_{X} – \widehat{ p}_{Y} \rightarrow N \left (p_{X}-p_{Y};  \displaystyle \sqrt { \displaystyle \frac { \widehat {p}_{X}  \widehat{ q}_{X} }{n_{X}} +  \displaystyle \frac { \widehat {p}_{Y}  \widehat{ q}_{Y} }{n_{Y}}} \right )      \)

o

\(  \displaystyle \frac{ ( \widehat {p}_{X} – \widehat{ p}_{Y})  – ( p_{X} –  p_{Y})}{   \displaystyle \sqrt { \displaystyle \frac { \widehat {p}_{X}  \widehat{ q}_{X} }{n_{X}} +  \displaystyle \frac { \widehat {p}_{Y}  \widehat{ q}_{Y} }{n_{Y} }  }    } \rightarrow  N(0,1) \)

para \( n_{X} \) y \( n_{Y} \) grandes

Fijado un nivel de significación α, la región de no rechazo para el contraste bilateral es \(  (-z_{α/2} , z_{α/2}) \)  y el estadístico de contraste, bajo la hipótesis nula \(  H_0 \equiv p_{X}-p_{Y}=(p_{X}-p_{Y})_{0} \) , adopta la forma

\( z_{exp} = \displaystyle \frac{ \left | ( \widehat {p}_{X} – \widehat{ p}_{Y})  – ( p_{X} –  p_{Y})_{0} \right |}{   \displaystyle \sqrt { \displaystyle \frac { \widehat {p}_{X}  \widehat{ q}_{X} }{n_{X}} +  \displaystyle \frac { \widehat {p}_{Y}  \widehat{ q}_{Y} }{n_{Y} }  }    }  \)

La regla de decisión es:

\(  \left.  \begin{array} \\  H_0 \equiv  p_{X}-p_{Y}=(p_{X}-p_{Y})_{0} \\  H_1 \equiv p_{X}-p_{Y} \neq (p_{X}-p_{Y})_{0} \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\    Si \hspace {.2cm} z_{exp}<z_{α/2 } \Rightarrow \hspace {.2cm} No \hspace {.2cm} se \hspace {.2cm} rechaza \hspace {.2cm} H_0  \\  Si \hspace {.2cm} z_{exp} \geq z_{α/2} \Rightarrow \hspace {.2cm} Se \hspace {.2cm} rechaza \hspace {.2cm}  H_0   \\ \end{array} \right. \)

Ejemplo 10.13. Se sospecha que añadiendo al tratamiento habitual para la curación de una determinada enfermedad un medicamento A, se consigue mayor número de curaciones. Tomamos dos grupos de enfermos de 100 individuos cada uno. A un grupo se le suministra el medicamento A y se curan 60 enfermos y al otro grupo no se le suministra, curándose 55 enfermos ¿Es efectivo el tratamiento A en la curación de la enfermedad, al nivel de significación del 1%?

Respuesta:

\(  \left.  \begin{array} \\  H_0 \equiv  p_{X} \leq p_{Y}   \\  H_1 \equiv  p_{X} > p_{Y}   \\ \end{array} \right \} \rightarrow   \left \{  \begin{array} \\    z_{exp}=  \displaystyle \frac{  \widehat {p}_x – \widehat {p}_y } {  \displaystyle \sqrt { \displaystyle \frac {\widehat {p}_x \widehat {q}_x} {n_{x }  } + \displaystyle \frac{ \widehat {p}_y \widehat {q}_y}{n_{y}}    }    }    =   \displaystyle \frac{0.6 – 0.55 } { \displaystyle \sqrt { \displaystyle \frac {0.6 \times 0.4 + 0.55 \times 0.45} {100 }     }       } = 0.716  \\    z_{α} = z_{0.01} = 2.33 >  z_{exp} \Rightarrow No \hspace {.2cm} se \hspace {.2cm} rechaza \hspace {.2cm}  H_0 \Rightarrow  \end{array} \right. \)

Podemos afirmar que el medicamento A no consigue un mayor número de curaciones.

Ejemplo 10.14. Se quiere comprobar la efectividad de una vacuna contra una enfermedad. Para ello se suministró la vacuna a 100 animales y se les comparó con un grupo testigo de otros 100. A los 200 se les contagió la enfermedad. Entre los vacunados murieron 8 como resultado de la enfermedad y del grupo testigo hubo 20 muertos. ¿Podemos concluir que la vacuna es eficaz en reducir la tasa de mortalidad?

Respuesta:

\( p_{X} \): “Probabilidad de morir con la vacuna”

\( p_{Y} \): “Probabilidad de morir sin la vacuna”

\(  \left.  \begin{array} \\  H_0 \equiv  p_{X} \geq p_{Y}   \\  H_1 \equiv  p_{X} < p_{Y}   \\ \end{array} \right \} \rightarrow   \left \{  \begin{array} \\    z_{exp}=  \displaystyle \frac{  \widehat {p}_x – \widehat {p}_y } {  \displaystyle \sqrt { \displaystyle \frac {\widehat {p}_x \widehat {q}_x} {n_{x }  } + \displaystyle \frac{ \widehat {p}_y \widehat {q}_y}{n_{y}}    }    }    =   \displaystyle \frac{ \displaystyle \frac{8}{100} – \displaystyle \frac{20}{100} } { \displaystyle \sqrt { \displaystyle \frac {0.08 \times 0.92 + 0.2 \times 0.8} {100 }     }       } = -2.48  \\    -z_{α} = – z_{0.05} = -1.645 >  z_{exp} \Rightarrow  Se \hspace {.2cm} rechaza \hspace {.2cm}  H_0 \Rightarrow  \end{array} \right. \)

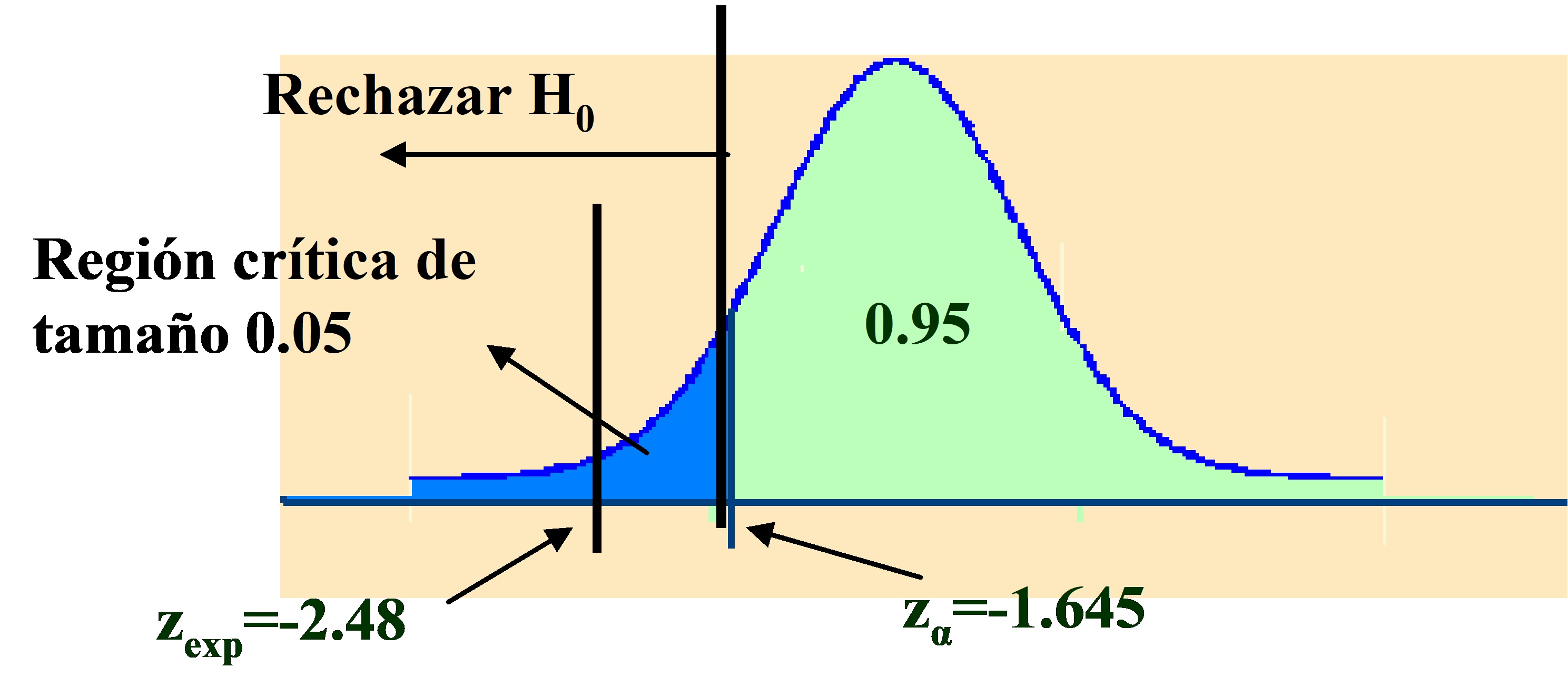
Figura 10.14

Se rechaza \( H_0 \) por lo tanto la vacuna es eficaz en reducir la tasa de mortalidad

Contrastes de comparación de dos varianzas

Consideramos dos poblaciones normales \(  N(μ_{X}, σ_{X}) \)  y \(  N(μ_{Y}, σ_{Y})  \) cuyas varianzas \(  σ_{X}^{2} \)  y \(  σ_{Y}^{2} \)  son desconocidas. El objetivo es probar uno de los siguientes contrastes de hipótesis

\(  \begin{array}{ccccc} H_0 \equiv  σ_{X}^{2}=σ_{Y}^{2}  &  &  H_0 \equiv σ_{X}^{2} \leq σ_{Y}^{2} &  & H_0 \equiv σ_{X}^{2} \geq σ_{Y}^{2} \\ & o & & o & \\  H_1 \equiv  σ_{X}^{2} \neq σ_{Y}^{2} &  &  H_1 \equiv  σ_{X}^{2} > σ_{Y}^{2} &  &  H_1 \equiv  σ_{X}^{2} < σ_{Y}^{2} \end{array}  \)

El estadístico de contraste adopta distintas formas dependiendo de que la media sea conocida o no.

a) Media poblacional conocida

Sabemos que

\( \displaystyle \frac{ n_{Y}} {n_{X}} \displaystyle \frac{σ_{Y}^{2}} {σ_{X}^{2}} \displaystyle \frac{ \displaystyle \sum_{i=1}^{n_{X}}(X_{i}-μ_{X})^{2} } { \displaystyle \sum_{j=1}^{n_{Y}}(Y_{j}-μ_{Y})^{2}} \rightarrow F_{n_{X},n_{Y}} \)

y si \( H_0 \)  es cierta entonces

\( \displaystyle \frac{ n_{Y}} {n_{X}} \displaystyle \frac{ \displaystyle \sum_{i=1}^{n_{X}}(X_{i}-μ_{X})^{2} } { \displaystyle \sum_{j=1}^{n_{Y}}(Y_{j}-μ_{Y})^{2}} \rightarrow F_{n_{X},n_{Y}} \hspace{2cm} [10.7] \)

Fijado un nivel de significación α, el estadístico de contraste \(  F_{exp} \), bajo la hipótesis nula \(  H_0 \equiv  σ_{X}^{2}=σ_{Y}^{2} \), sigue una distribución \( F_{n_{X}, n_{Y}} \) y tiene la expresión ([10.7])

Hipótesis alternativa Regla de decisión

\(  \begin{array}{| l| l |} \hline Hipótesis \hspace{ .2cm} alternativa & Regla \hspace{ .2cm} de \hspace{ .2cm} decisión \\ \hline
H_1 \equiv σ_{X}^{2} \neq σ_{Y}^{2} & Rechazar \hspace{ .2cm} H_0  \hspace{ .2cm}cuando \hspace{ .2cm} F_{exp} \geq  F_{α/2;n_X,n_Y} \hspace{ .2cm} o \hspace{ .2cm} F_{exp} \leq  F_{1-α/2;n_X,n_Y} \\ \hline H_1 \equiv σ_{X}^{2} > σ_{Y}^{2}  & Rechazar \hspace{ .2cm} H_0 \hspace{ .2cm} cuando \hspace{ .2cm} F_{exp} \geq F_{α;n_X,n_Y} \\  \hline H_1 \equiv σ_{X}^{2} < σ_{Y}^{2} & Rechazar  \hspace{ .2cm} H_0 \hspace{ .2cm} cuando  \hspace{ .2cm} F_{exp} \leq F_{1-α;n_X,n_Y} \\ \hline \end{array}  \)

b) Media poblacional desconocida

Sabemos que

\(  \displaystyle \frac{S_{X}^{2}}{S_{Y}^{2}} \displaystyle \frac{σ_{Y}^{2}}{σ_{X}^{2}} \rightarrow F_{n_{X}-1,n_{Y}-1} \)

y si \(  H_0 \) es cierta entonces

\(  \displaystyle \frac{S_{X}^{2}}{S_{Y}^{2}}  \rightarrow F_{n_{X}-1,n_{Y}-1}  \hspace{2cm} [10.8 ] \)

Fijado un nivel de significación α, el estadístico de contraste \( F_{exp}\), bajo la hipótesis nula \( H_0 \equiv σ_{X}^{2}=σ_{Y}^{2} \), sigue una distribución \( F_{n_{X}-1,n_{Y}-1}\) y tiene la expresión ([10.8]).

Se adopta la misma regla de decisión que el caso anterior pero teniendo en cuenta que en esta situación la distribución F- Snedecor tiene \( n_{X}-1 \) y \( n_{Y}-1 \) grados de libertad.

Ejemplo 10.15. En el desarrollo de la arteroesclerosis cardiaca y coronaria un nivel de colesterol elevado es un factor de alto riesgo, por ello es importante determinar los niveles a esperar en los diferentes grupos de edad. Se realizó un estudio para comparar el nivel de colesterol en varones de entre 20 y 29 años frente a mujeres del mismo grupo de edad. Se obtuvieron los siguientes resultados:

Hombres: H: \( n_{H} =25  \hspace{2cm} \overline{x}_{H}=167.16 \hspace{2cm } s_{H}=30 \)
Mujeres: M: \( n_{M} =31 \hspace{2cm} \overline{x}_{M}=178.12 \hspace{2cm} s_{M}=32 \)

¿Se puede considerar que la dispersión en ambas poblaciones es la misma?

Respuesta:

\(  \left.  \begin{array} \\  H_0 \equiv  σ_{H}^{2} = σ_{M}^{2}   \\  H_1 \equiv  σ_{H}^{2} \neq  σ_{M}^{2}   \\ \end{array} \right \} \rightarrow   \left \{  \begin{array} \\    F_{exp}=  \displaystyle \frac{  s_{H}^{2} } {  s_{M}^{2}   }    =   \displaystyle \frac{ (30)^{2}} {(32)^{2}} = 0.8789  \\    F_{0.025;24,30} = 2.14 \\   F_{0.975;24,30} =  \displaystyle \frac{ 1}{F_{0.025;30,24} } \end{array} \right. \)

\(  F_{0.975;24,30}=0.45<F_{exp}<F_{0.025;24,30}=2.14 \rightarrow \) No se rechaza \(  H_{0} \); la dispersión en ambas poblaciones es la misma.

 

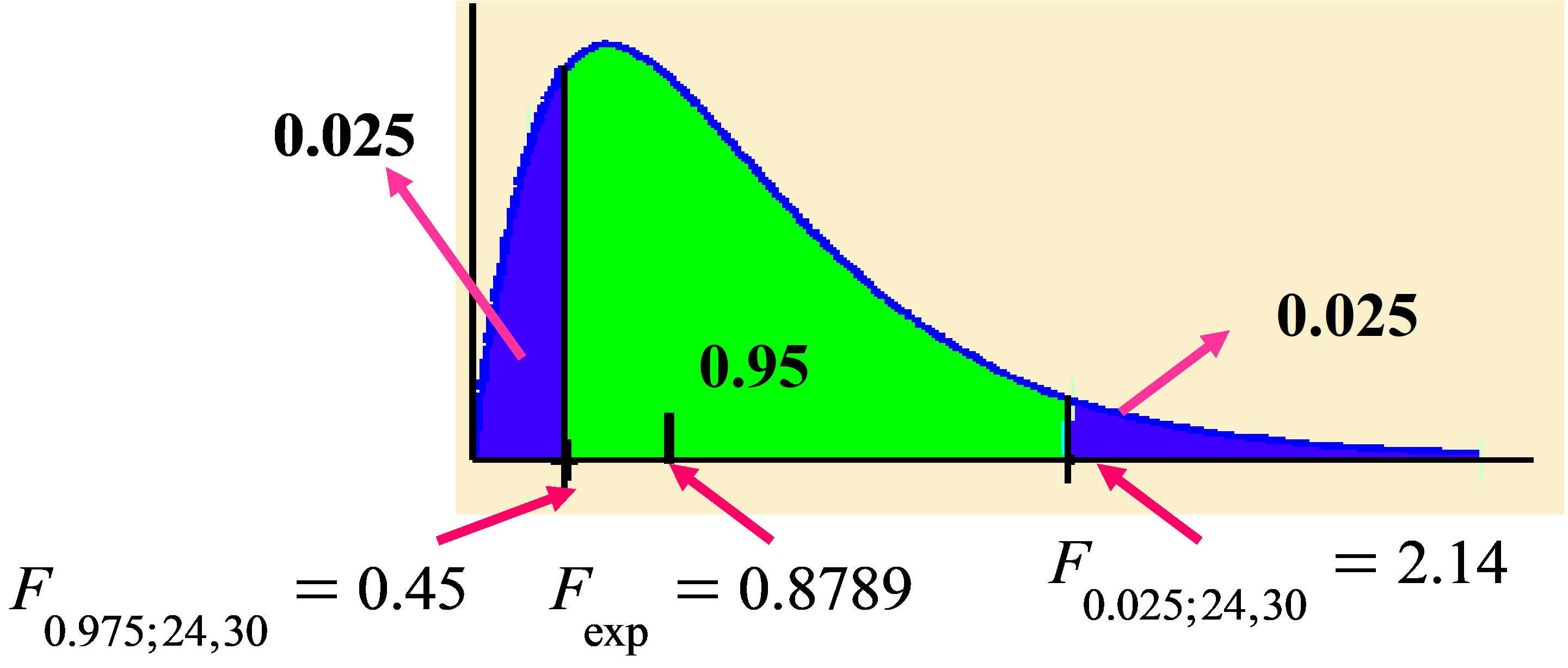
Figura 10.15

Ejemplo 10.16. Un instituto de dietética quiere comparar dos dietas. Se selecciona una muestra de 50 individuos, al azar de una población de personas comparables con exceso de peso. A 25 personas se les suministra la dieta A y a los 25 restantes la dieta B. Las pérdidas de peso expresadas en Kg. al cabo de una semana son las siguientes:

Dieta A: \(  \overline{x}_{A}=4.3 \) Kg \( \hspace{2cm}s_{A}=1.4 \) Kg

Dieta B: \(  \overline{x}_{B}=3.6 \) Kg \( \hspace{2cm}s_{B}=1.1\) Kg

Suponiendo normal la variable pérdida de peso, ¿hay razón suficiente para admitir que la media del peso de las personas que se les suministra la dieta A es mayor que las corres-pondientes de la dieta B? (nivel de confianza del 5%).

Respuesta: Hay que realizar un contraste para la igualdad de medias pero en primer lugar debemos contrastar las varianzas:

\(  \left.  \begin{array} \\  H_0 \equiv  σ_{A}^{2} = σ_{B}^{2}   \\  H_1 \equiv  σ_{A}^{2} \neq  σ_{B}^{2}   \\ \end{array} \right \} \rightarrow   \left \{  \begin{array} \\    F_{exp}=  \displaystyle \frac{  s_{A}^{2} } {  s_{B}^{2}   }    =   \displaystyle \frac{ (1.4)^{2}} {(1.1)^{2}} = 1.62  \\    F_{α/2;n_{A}-1,n_{B}-1} = F_{0.025;24,24} = 2.27 >  F_{exp} \Rightarrow No  \hspace {.2cm} se \hspace {.2cm} rechaza \hspace {.2cm}  H_0 \Rightarrow  \end{array} \right. \)

A continuación se realiza el contraste de igualdad de medias de dos poblaciones normales con varianzas desconocidas pero iguales y muestras pequeñas.

\(  \left.  \begin{array} \\  H_0 \equiv  μ_{A}  \leq μ_{B}   \\  H_1 \equiv  μ_{A}> μ_{B}    \\ \end{array} \right \} \rightarrow   \left \{  \begin{array} \\    t_{exp}=  \displaystyle \frac{  \overline {x}_{A} – \overline {x}_{B}  } { s_{p} \displaystyle \sqrt { \displaystyle \frac {1} {n_{A }  } + \displaystyle \frac{ 1}{n_{B}}    }    }    =   \displaystyle \frac{  4.3 – 3.6  } { 1.585 \displaystyle \sqrt { \displaystyle \frac {1} {25 } + \displaystyle \frac{1}{25}    }       } = 1.965  \\    t_{α;n_{A}+n_{B}-2} = t_{0.05;48} = 2.018  >  t_{exp} \Rightarrow \hspace {.2cm} No \hspace {.2cm} se \hspace {.2cm} rechaza \hspace {.2cm}  H_0   \\ \end{array} \right. \)

siendo

\( s_{p}^{2}= \displaystyle \frac{ (n_{A}-1)s_{A}^{2}+(n_{B}-1)s_{B}^{2}} {n_{A}+n_{B}-2}= \displaystyle \frac{ 24(1.96+1.21)} {48}=1.585 \)

El peso de la personas que siguen la dieta A es menor que el peso de aquellas que siguen la dieta B.

Contraste de hipótesis de comparación de dos medias para datos emparejados (apareados)

En las muestras apareadas, cada observación de una muestra está emparejado con una observación de la otra muestra, por lo tanto consideramos parejas de valores (x,y).

Supongamos que \( X \) e \( Y \) son dos variables aleatorias tales que \( X \rightarrow N(μ_{X}, σ_{X}) \) e \( Y \rightarrow N(μ_{Y}, σ_{Y})  \) y consideremos la diferencia de poblaciones \( D=X-Y \) . Entonces,  \( D \rightarrow N(μ_{D}, σ_{D}) \)

Se selecciona una muestra aleatoria de diferencias, \( D_{i}=X_{i}-Y_{i} \hspace{.2cm}, \hspace{.2cm} i=1,2, \cdots, n \)

El valor medio de D es la diferencia de los valores medios de X e Y:

\( μ_{D}=E(D)=E(X-Y)=E(X)-E(Y)=μ_{X}-μ_{Y} \)

La varianza de D es:

\( σ_{D}^{2}=Var(D)=Var(X-Y) \)

Contrastar la hipótesis nula \(  H_0 \equiv μ_{X}-μ_{Y}=0 \) es equivalente a contrastar la hipótesis \( H_0 \equiv  μ_{D}=0 \), por lo tanto el contraste original de dos medias se reduce al problema de una media y el estadístico de contraste está basado en la muestra de diferencias:

\( \displaystyle \frac{ \overline {D}} {S_{D}/ \sqrt{n}} \)

que, bajo la Hipótesis \( H_0 \), sigue una distribución t de Student con n-1 grados de libertad.

Ejemplo 10.17. Se realiza un estudio, en el que participan 10 individuos, para investigar el efecto del ejercicio físico en el nivel de colesterol en plasma. Antes del ejercicio se tomaron muestras de sangre para determinar el nivel de colesterol de cada individuo. Después, los participantes fueron sometidos a un programa de ejercicios. Al final de los ejercicios se tomaron nuevamente muestras de sangre y se obtuvo una segunda lectura del nivel de colesterol. Los resultados se muestran a continuación:

\(  \begin{array}{| l| cccccccccc |} \hline  Nivel \hspace{ .2cm}previo & 182 & 230 & 160 & 200 & 160 & 240 & 260 & 480 & 263 & 240  \\ \hline Nivel \hspace{ .2cm} posterior & 190 & 220 & 166 & 150 & 140 & 220 & 156 & 312 & 240 & 250 \\ \hline \end{array}  \)

Se quiere saber si el ejercicio físico ha reducido el nivel de colesterol para un nivel de confianza del 95%

Respuesta:

\(  \begin{array}{| l| cccccccccc |} \hline  Nivel \hspace{ .2cm}previo & 182 & 230 & 160 & 200 & 160 & 240 & 260 & 480 & 263 & 240  \\ \hline Nivel \hspace{ .2cm} posterior & 190 & 220 & 166 & 150 & 140 & 220 & 156 & 312 & 240 & 250 \\ \hline d=x-y  & -8 & 10 & -6 & 50 & 20 & 20 &  44 &  168 &  20 & -10 \\ \hline \end{array}  \)

\(  \overline {d} = \displaystyle \frac{268} {10} =30.8 \hspace{2cm} ; \hspace{2cm} s_{d}= \displaystyle \frac{ \displaystyle \sum_{i=1}^{10}(d_{i}- \overline{d})}{n-1}= 52.36 \)

\(  \left.  \begin{array} \\  H_0 \equiv  μ_{D}  \leq 0   \\  H_1 \equiv  μ_{D}> 0   \\ \end{array} \right \} \rightarrow   \left \{  \begin{array} \\    t_{exp}=  \displaystyle \frac{  \overline {d}  } { S_{d} \displaystyle \sqrt {n}}    =   \displaystyle \frac{  30.8  } { 52.36 \sqrt { 10} } = 1.86  \\    t_{α;n-1} = t_{0.05;9} = 1.833 <  t_{exp} \Rightarrow Se \hspace {.2cm} rechaza \hspace {.2cm}  H_0   \\ \end{array} \right. \)

El nivel medio de colesterol se reducirá con el ejercicio físico.

Ejercicios propuestos: Relación X

1. El nivel medio de protrombina en una determinada población es conocido y resulta ser de 20 mg/100ml de plasma. Se toma una muestra de 40 pacientes que se sabe tienen deficiencia de vitamina K; los resultados han sido los siguientes: \( \overline{x}=18.50 \) mg/100ml y s=4 mg/100ml. Se pregunta si es la muestra comparable con la población a un nivel de significación del 0.05. (Sol: Rechazar \( H_0 \)).

2. Unos laboratorios farmaceúticos realizan unos estudios para determinar el contenido en grs. de ungüento en unos frascos de un medicamento. Para ello se toman 10 frascos y se determina el contenido en grs. de ungüento en cada uno de los frascos obteniendo los siguientes resultados:

\(  \begin{array}{| l| cccccccccc |} \hline  Tubo & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10  \\ \hline Contenido \hspace{ .2cm} en  \hspace{ .2cm} gramos & 5.2 & 4.9 & 5 & 5.1 & 5.2 & 4.8 & 4.9 & 5.3 & 4.6 & 5.4 \\ \hline \end{array}  \)

Sabemos por otras muchas determinaciones que la desviación típica de la población es de 0.10 grs. y queremos averiguar si los valores anteriores son compatibles con la media μ=5 grs. para la población, supuesta ésta Normal. (Sol: No rechazar \( H_0 \)).

3. En un anuncio publicitario se indica que un determinado tipo de agua reduce peso. Doce individuos que decidieron tomar dicha marca de agua en sustitución de la que habitualmente tomaban, manteniendo intacta el resto de la dieta alimenticia, sufrieron las variaciones de peso, al cabo de cierto tiempo, dadas en la tabla, Se puede admitir que el anuncio es correcto. (Sol: No rechazar \( H_0 \) ).

\(  \begin{array}{| l| cccccccccccc |} \hline  Individuo & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12  \\ \hline Variación \hspace{ .2cm} de  \hspace{ .2cm} peso & 0.2 & 0 & 1 & 0.6 & -0.5 & -0.6 & -1 & 0.6 & 1 & 0.5 & -0.4 &  -0.5  \\ \hline \end{array}  \)

4. Un laboratorio farmacéutico afirma que un calmante de su fabricación quita la jaqueca en14 minutos en los casos corrientes. Con el fin de comprobar estadísticamente esta afirmación, se eligen al azar 18 pacientes con jaqueca y se toma como variable respuesta en el experimento el tiempo transcurrido entre la administración del calmante y el momento que desaparece la jaqueca. Los resultados en la muestra fueron \( \overline {x} =19 \) minutos y s=7 minutos. Se pide comprobar la afirmación del laboratorio a un nivel de significación de 0.05. (Sol: SIG).

5. El nivel medio de nistamina en un ungüento, se supone conocido a través de una larga serie de análisis, es igual a 2.5 millones de unidades por gramo. Su distribución sigue la ley Normal. Se toma una muestra de 16 ungüentos, que nos dan un contenido medio de nistamina de 2.8 millones de unidades por gr. con una desviación típica muestral de 0.4 millones de unidades por gramo ¿ Son estos resultados compatibles con la media supuesta para la población? (Sol: SIG).

6. Se están utilizando normalmente en una granja avícola dos tipos de piensos compuestos A y B. Queriendo averiguar si la media de engorde con ambos piensos es idéntica, para un nivel de significación del 5%, se alimenta a 20 aves durante cierto tiempo con el pienso A y se obtiene una ganancia media de peso por ave de 0.4 Kg. con una desviación típica de 0.2 Kg. Simultáneamente a otras 20 aves se les alimenta con el pienso B y se obtiene un engorde medio de 0.5 Kg. con una desviación típica de 0.3 Kg. Suponemos que las variables objeto de estudio, engorde con cada uno de los piensos, son normales y con la misma varianza. Compárense los dos piensos compuestos. (Sol: NO SIG).

7. Noventa inadaptados son ingresados en centros de rehabilitación. De ellos 50 en el Centro A, donde consiguieron su recuperación en un plazo medio de 150 días, con una desviación típica de 30 días. Los 40 restantes fueron ingresados en otro Centro B, donde se recuperaron en 160 días con una desviación típica de 25 días ¿Se puede considerar que el Centro de Rehabilitación A es más adecuado que el B, para conseguir una recuperación más rápida? ¿Bajo qué hipótesis? (Sol: SIG).

8. Se quieren comparar dos poblaciones de ranas pipiens aisladas geográficamente. Para ello se toman dos muestras de ambas poblaciones y se les mide la longitud del cuerpo expresada en milímetros, obteniéndose los siguientes resultados:  \( \overline {x}_1=74; s^{2}=225; n_1=42; \overline {x}_2=78; s^{2}=169; n_2=56 \). Contrastar las hipótesis de igualdad de medias con un nivel de significación del 5%.(Suponiendo que la longitud se distribuya según una Normal) (Sol: NO SIG)

9. Un laboratorio fabrica dos tipos de somníferos A y B. Se toman dos grupos análogos de enfermos de insomnio formado por 80 y 100 individuos respectivamente, se suministra a los enfermos del primer grupo el somnífero A y a los del segundo grupo, el B. El número medio de horas de sueño para los enfermos del primer grupo fue de 7.84 con una cuasidesviación típica de 0.90 y para los del segundo grupo fue de 6.90 y 1.30 respectivamente ¿Se puede decir que la diferencia entre los números medios de horas de sueño es significativa? (Sol: SIG)

10. Se está haciendo un estudio sobre la presión arterial. Se consideran las presiones sistólicas de un grupo de niños con uno de sus padres hipertensos y otro grupo de niños cuyos padres tiene presión normal. Los datos han sido los siguientes: \( \overline {x}_1 =105.8; s_{1}^{2}=50.51; n_1=10; \overline {x}_2=97.2; s_{2}^{2}=50.41; n_2=9 \). Se quiere comprobar estadísticamente si el tener progenitores hipertensos influye en la presión sistólica. (α=0.05).(Sol: SIG).

11. Se sabe que la duración de un determinada enfermedad sigue una ley Normal. Para la curación de dicha enfermedad se emplean dos tipos de antibióticos y se desea comprobar estadísticamente cuál de los dos es más eficaz con respecto a la duración de la enfermedad. A tal fin se observan 6 enfermos a los que se les aplica el primer antibiótico y 5 enfermos a los que se les aplica el segundo. Los resultados han sido los siguientes:

\( \overline {x}_1=12 \) días; \( s_{1}^{2}=16;n_1=6 \)

\(  \overline{x}_2=15 \) días; \( s_{2}^{2}=16;n_2=95 \)

Se pregunta cuál de los dos antibióticos es más eficaz a un nivel de significación 0.025. (Sol: NO SIG).

12. Una central lechera recibe diariamente leche de dos granjas A y B. Deseando estudiar la calidad de los productos recibidos se eligen dos muestras al azar de la leche suministrada por cada una de las granjas, se analiza el contenido de grasa y se obtienen los siguientes resultados:

Granja A : \( \overline {x}_1=0.305; s_{1}^{2}=0.034; n_1=12 \)

Granja B : \( \overline {x}_2=0.318; s_{2}^{2}=0.027; n_2=16 \)

Se pide, bajo la hipótesis de normalidad de los datos: a) ¿Son las dos granjas semejantes desde el punto de vista del contenido en grasa de la leche que emiten a la central lechera?; b) ¿ Son las varianzas poblacionales iguales? (Soluciones: a) NO SIG; b) NO SIG).

13. Un laboratorio farmacológico afirma que un analgésico que fabrica es efectivo en la eliminación del dolor de estómago durante 12 horas en un 95% de los casos. Se tomó una muestra de 150 individuos que padecían de dolor de estómago y se les suministró el analgésico citado, siendo efectivo para 132 individuos. ¿Qué podemos opinar acerca de la afirmación del laboratorio para un nivel de significación del 5%? (Sol: SIG).

14. Se quiere estudiar si el 85% de los niños con dolor torácico tienen un ecocardiograma normal. Para ello, se toma una muestra de 139 niños con dolor torácico, de ellos 123 presentan un ecocardiogramas normal. ¿Apoyan los datos la hipótesis? (Solución: no se debe rechazar que la proporción de niños con ecocardiograma normal sea 0.85).

15. En una empresa de fundición se recibe periódicamente mineral de hierro procedente de dos yacimientos distintos A y B. Para estudiar la calidad del mineral recibido se extraen dos muestras y se analiza la riqueza de hierro, obteniendo los siguientes resultados en %

A: 43, 45, 42, 35, 37, 38, 33, 38, 41, 43

B : 39, 36, 35, 37, 40, 39, 40, 38, 35, 39, 38, 34

Suponiendo normal la distribución de la riqueza del mineral, se pide a un nivel α = 0.05: a) ¿se puede admitir que la diferencia de varianzas es significativa ; b) Hay suficiente evidencia para afirmar que la riqueza en hierro del yacimiento A es superior al del yacimiento B (Solución: a) No; b) No se puede afirmar que la riqueza en hierro del yacimiento A es superior al del yacimiento B.).

16. Entre los pacientes con cáncer de pulmón, el 90% o más muere generalmente en el espacio de tres años. Como resultado de nuevas formas de tratamiento, se cree que esta tasa se ha reducido. En un reciente estudio sobre 150 pacientes diagnosticados de cáncer de pulmón, 128 murieron en el espacio de tres años. ¿Se puede afirmar que realmente ha disminuido la tasa de mortalidad al nivel α=0.1?(Sol: Si se puede afirmar)

17. Ante una epidemia, un granjero sospecha que el número de aves jóvenes muertas es inferior al de aves adultas. Para salir de dudas, aísla una muestra de 200 aves jóvenes y al cabo de un mes se han muerto 58, igualmente aísla 150 aves adultas muriendo en el mismo periodo 36. ¿Qué conclusión puede sacar el granjero, con un α = 0.05 ? (Sol: NO SIG).

18. En un estudio de características corporales de las gaviotas de pico anillado, la variable considerada es la longitud del pico. Se dispone de los datos mostrados en la tabla adjunta ¿Hay evidencia para sostener el argumento de que la longitud media del pico de los machos sea mayor que la de las hembras? (para un nivel α = 0.02) (Sol: Si hay evidencia)

Hembras: \(  n_1=51; \overline {x}_1=59.1; s_1 = 1.9 \)

Machos: \(   n_2=41; \overline {x}_2 = 65.2; s_2=2.0 \)

19. El índice de salubridad idóneo para que un agua mineral sea de calidad extra es de 75 o más. En una fuente explotada por un cierto fabricante se tomaron 16 muestras, dando un índice medio de salubridad de 74 y una desviación típica de 7.75. Bajo el supuesto de normalidad del índice de salubridad, ¿se puede permitir a este fabricante que embotelle con la etiqueta de calidad extra?

En otro manantial cercano se llevó a cabo el mismo análisis con 25 muestras dando una salubridad media de 72 y una desviación típica de 6.85 ¿Puede admitirse que el agua de este manantial es de la misma calidad que la de la fuente anterior? (Soluciones: a) Debe permitirse al fabricante el etiquetado extra; b) No se puede rechazar que ambos manantiales tienen la misma calidad).

20. Se lleva a cabo un estudio de dos tipos de tratamientos por fármacos para su utilización potencial en transplantes de corazón. El fin de los fármacos es actuar como inmunosupresores (reprimir la tendencia natural del cuerpo a rechazar el transplante). Las ratas ACI machos sirven como receptores. Se toman dos muestras de este tipo de ratas, y a cada grupo se le aplica uno de los tratamientos. La variable de interés es X, tiempo de supervivencia en horas. Se obtuvieron los siguientes resultados en horas:

Grupo A : \(  n_1=8; \overline {x}_1=1.432; s_{1}^{2}=436  \)

Grupo B : \( n_2=21;  \overline {x}_2=1.310; s_{2}^{2}=382 \)

Haciendo las suposiciones apropiadas de normalidad e independencia, contrastar si existen diferencias entre los tiempos medios de supervivencia, al nivel 0.05. (Sol: Ambos tratamientos son igual de efectivos).

21. Una organización de protección al consumidor llevó a cabo un estudio para comparar la producción de tomates con 2 tipos de fertilizantes. Cada fertilizante fue instalado en dos invernaderos independientes y la producción (Ton/ha) fue registrada para varias cosechas, obteniendo los siguientes datos:

Fertilizante I: 1, 2, 3, 3, 1, 5, 4, 3

Fertilizante II: 5, 3, 1, 6, 5, 4, 5, 6. 7

a) Se considera que una cosecha ha sido provechosa cuando la recolección excede la cantidad de 3.5 Ton/ha. De las 17 cosechas anteriores se ha tomado una observándose que ha sido provechosa, ¿cuál es la probabilidad de que haya sido producida con el fertilizante I?

b) Se sabe por experiencias previas que la probabilidad de que una cosecha sea provechosa con fertilizante I es 0.2. ¿Cuál es la probabilidad de que en 10 cosechas observadas al menos 1 haya sido provechosa? ¿Cuál es la probabilidad de que en 100 cosechas observadas al menos 12 sean provechosas?

c) Suponiendo normalidad e independencia entre las muestras, ¿se puede consi-derar que no hay diferencia entre ambos fertilizantes respecto a la cantidad de producción? (α = 0.05).

d) Construir un intervalo de confianza para la diferencia de medias cuando las varianzas son desconocidas pero iguales al nivel de confianza 1-α. Aplicarlo para estudiar el comportamiento de las cantidades medias producidas por ambos fertilizantes al nivel de confianza 0.95.

22. Se realiza un estudio a 36 individuos para determinar el efecto de un medidor para ayudar a los diabéticos a controlar sus niveles de glucosa en sangre. Se obtuvieron los niveles de glucosa para cada paciente antes y después de utilizar el medidor. Se registró una diferencia muestral media \( \overline{d}=2.78 \) y una cuasidesviación típica muestral \( s_{d}=6.05 \). ¿Hay prueba suficiente para saber si el medidor es efectivo para ayudar a los pacientes a reducir sus niveles de glucosa? (Sol: Si es efectivo)

23. Se realiza un estudio para investigar el efecto del ejercicio físico sobre el nivel de triglicéridos, en el que participaron once individuos. Antes del ejercicio se tomaron muestras de sangre para determinar el nivel de triglicéridos de cada participante. Después, los individuos fueron sometidos a un programa físico que se centraba en carreras y marchas diarias. Al final del periodo de ejercicios, se tomaron nuevamente muestras de sangre y se obtuvo una segunda lectura del nivel de triglicéridos en sangre. Los datos se muestran en la tabla adjunta. Se pensó que el programa de ejercicios físicos podría reducir del nivel de triglicéridos en sangre. ¿Sostienen estos datos el argumento de los investigadores? (Supóngase normalidad) (Solución: Si puede reducirlo).

\(  \begin{array}{| l| ccccccccccc|} \hline  Nivel \hspace{ .2cm}previo & 198 & 210 & 194 & 220 & 138 & 220 & 219 & 161 & 210 & 313 & 226  \\ \hline Nivel \hspace{ .2cm} posterior & 65 & 77 & 94 & 73 & 37 & 131 & 77 & 24 & 99 & 321 & 57 \\ \hline \end{array}  \)

Autora: Ana María Lara Porras. Universidad de Granada

Estadística para Biología y Ciencias Ambientales. Tratamiento informático mediante SPSS. Proyecto Sur Ediciones.