CONTRASTES DE HIPÓTESIS BASADOS EN LA CHI-CUADRADO

Introducción

En el Capítulo 10 se han tratado los contrastes de hipótesis acerca de parámetros poblacionales tales como \( μ \), \( σ^{2} \) y \( p \), de ahí el nombre de Contrastes Paramétricos. En el presente capítulo se estudian los contrates de hipótesis en los que la característica que se desconoce es alguna propiedad de la distribución que se muestrea. Además se discutirán los contrastes de dependencia o independencia entre caracteres cualitativos. Estos contrastes reciben el nombre de Contrastes No-Paramétricos.

Así, uno de los objetivos del presente capítulo es el estudio de contrates de hipótesis para determinar si una población tiene una distribución teórica específica. La técnica que nos introduce a estudiar esas cuestiones se llama Contraste de la Chi-cuadrado para la Bondad de Ajuste. Una variación de este contraste se emplea para resolver los Contrastes de Independencia. Tales contrastes se utilizan para determinar si dos características están relacionadas o son independientes es decir, si existe o no asociación entre dos variables. Así, mediante los contrastes de independencia responderemos a preguntas del siguiente tipo: ¿Hay asociación entre la preferencia política y los ingresos? ¿entre el hábito de fumar y el cáncer de pulmón? ¿entre la drogadicción por vía parental y el SIDA? ¿entre la obesidad y la hipertensión? Y, por último estudiaremos otra variación del contraste de la bondad de ajuste llamado Contraste de Homogeneidad, este contraste se utiliza para estudiar si diferentes poblaciones, son similares (u homogéneas) con respecto a alguna característica. Por ejemplo, queremos saber si las proporciones de votantes que favorecen al candidato A, al candidato B o los que se abstuvieron son las mismas en dos ciudades. En esencia los aspectos nuevos que se van abordar son:

• Conformidad de una distribución experimental y una distribución teórica mediante contrastes de hipótesis en los que se confrontan los resultados de un experimento con una teoría. Son contrastes para examinar si los datos experimentales, los resultados proporcionados por una muestra aleatoria, son conformes con una determinada distribución teórica dada de antemano. Como, mediante estos contrastes se trata de comprobar si los datos experimentales se ajustan bien a una cierta distribución, dichos contrastes reciben el nombre de Contrastes para la Bondad de Ajuste a Distribuciones.
• Dependencia o independencia entre dos caracteres cualitativos mediante contrastes de hipótesis en los que se comprueban si dos características cualitativas están relacionadas entre sí, estos contrastes son los Contrastes para la Independencia de dos Caracteres Cualitativos.
• Comprobar si varias muestras de una carácter cualitativo se pueden considerar procedentes de una misma población. Dicha comprobación se realiza mediante los Contrastes de Homogeneidad de Varias Muestras Cualitativas.

En los contrastes de Independencia y en los contrates de homogeneidad el tipo de datos está caracterizado por el hecho de que cada una de las observaciones está incluida en una de varias categorías mutuamente excluyentes. El interés se centra en el número de observaciones que hay dentro de cada categoría. El objetivo es determinar si las frecuencias de la categoría observada tiende a apoyar o rechazar una hipótesis planteada.

Hemos agrupado estos temas en este capítulo porque el denominador común a todos ellos es que su tratamiento estadístico se aborda mediante la distribución Chi-cuadrado.

Contrastes para la bondad de ajuste

El objetivo de los Contrastes de Bondad de Ajuste a Distribuciones consiste en determinar a partir de un conunto de datos muestrales si estos son consistentes con una distribución de probabilidad teórica.

Los datos observados (o experimentales) y los datos obtenidos mediante una cierta distribución de probabilidad, datos teóricos, difieren unos de otros, ya que raramente el ajuste de entre ambos tipos de datos es perfecto. Mediante los Contrastes de Bondad de Ajuste se determina si las diferencias existentes entre las frecuencias observadas y las teóricas son únicamente debidas al azar al tomar la muestra.

Consideramos una variable aleatoria \( X \) discreta o continua y una muestra aleatoria de tamaño n de la distribución de dicha variable agrupada en k clases exhaustivas y mutuamente excluyentes y sea \(  n_{i} \), \(  i=1, 2, \cdots, k \) la frecuencia absoluta de la i-ésima clase (el número de observaciones de la i-ésima clase).

Supongamos una cierta distribución teórica para \( X \) cuyos parámetros poblacionales los estimamos a partir de los datos muestrales. Si denotamos por\( p_{i} \) la probabilidad teórica asociada a la clase \( i \) entonces \( np_{i} \) será la frecuencia absoluta teórica asociada a la clase \( i \). En forma tabular se puede poner de la siguiente forma:

\(  \begin{array}{| c| c|c|c|c|} \hline  Clases  &  Marca \hspace{ .2cm} de \hspace{ .2cm} clase  & Fre. \hspace{ .2cm} absolutas &  Probabilidades & Fre. \hspace{ .2cm}  absolutas \\     &   &    empíricas \hspace{ .2cm} n_{i}   & teóricas \hspace{ .2cm} p_{i} & teóricas \\  & & & & (Valores \hspace{ .2cm} Esperados) \\ \hline 1 &   x_1  &  n_1  &   p_1 &    np_1 \\ \hline 2 &   x_2  &  n_2  &   p_2 &    np_2  \\ \hline \vdots & \vdots & \vdots & \vdots & \vdots  \\ \hline  i & x_i  &  n_i  &   p_i &    np_i \\ \hline \vdots & \vdots & \vdots & \vdots & \vdots  \\ \hline k & x_k  &  n_k  &   p_k  &    np_k  \\ \hline &  & n &   1 &   n \\ \hline \end{array}  \)

Partiendo de una muestra de \( n \)  valores observados \(  x_1,x_2, \cdots ,x_{n} \) de una v.a. \( X  \) con distribución supuesta \(  F(x) \) , se plantea el siguiente contraste de hipótesis:

\(  H_0 \equiv  X \rightarrow  F(x)  \) (La distribución teórica está conforme con la distribución empírica)
\(  H_1  \equiv  X \) sigue otra distribución

que se resuelve mediante el siguiente estadístico de contraste propuesto por Pearson

\(  χ_{exp}^{2}= \displaystyle \frac {(n_1-np_1)^{2}}{np_1}+ \displaystyle \frac {(n_2-np_2)^{2}}{np_2} + \cdots +  \displaystyle \frac {(n_k-np_k)^{2}}{np_k}=  \displaystyle  \sum_{i=1}^{k}  \displaystyle \frac {(n_i-np_i)^{2}}{np_i}   \)

dicho estadístico, bajo la hipótesis nula, se distribuye aproximadamente según una \( χ^{2} \) con  \( k-r-1 \) grados de libertad

• r: es el número de parámetros estimados de los que depende la distribución teórica. Así, el número de grados de libertad está relacionado con el número de parámetros desconocidos de los que depende la distribución teórica, por ejemplo si la ley de probabilidad es una Normal, N(μ, σ), ambos parámetros desconocidos, el número de grados de libertad es k-2-1=k-3, si es una Poisson, P(λ), el número de grados de libertad es k-1-1=k-2.
• k: es el número de clases
• Si las frecuencias observadas se acercan a las correspondientes frecuencias esperadas, el valor \( χ_{exp}^{2} \) será pequeño, lo que indica un buen ajuste.
• Si las frecuencias observadas difieren considerablemente de las frecuencias esperadas, el valor \( χ_{exp}^{2} \) será grande y el ajuste será malo.

Un buen ajuste conduce a la aceptación de \( H_0 \) mientras que un mal ajuste conduce a su rechazo. La región crítica, por lo tanto, caerá en la cola derecha de la distribución Chi-cuadrada.

Para un nivel de significación α, la regla de decisión apropiada es:

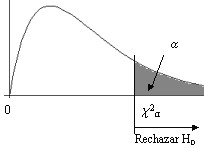  \(   \begin{array} \\   Si \hspace {.2cm} χ_{exp}^{2} < χ_{α;k-r-1}^{2} \Rightarrow No \hspace {.2cm} se \hspace {.2cm} rechaza \hspace {.2cm} H_0 \Rightarrow la  \hspace {.2cm} diferencia \\  entre \hspace {.2cm} la \hspace {.2cm} distr.  \hspace {.2cm} experimental \hspace {.2cm} y \hspace {.2cm} la \hspace {.2cm} teórica \hspace {.2cm} no \hspace {.2cm} es \hspace {.2cm} significativa \\ \\  Si \hspace {.2cm} χ_{exp}^{2} \geq  χ_{α;k-r-1}^{2} \Rightarrow Se \hspace {.2cm} rechaza\hspace {.2cm}  H_0 \Rightarrow la \hspace {.2cm} diferencia \hspace {.2cm} entre \\ la \hspace {.2cm} distr. \hspace {.2cm} experimental \hspace {.2cm} y \hspace {.2cm} la \hspace {.2cm} teórica \hspace {.2cm} es \hspace {.2cm} significativa \hspace {.2cm} y \hspace {.2cm} cuanto \\ mayor \hspace {.2cm} sea \hspace {.2cm} dicha \hspace {.2cm} diferencia \hspace {.2cm} mayor \hspace {.2cm} es \hspace {.2cm} la \hspace {.2cm} significación. \end{array} \)

El criterio de decisión que acabamos de describir se utiliza si cada una de las frecuencias esperadas es al menos igual que 5. Si la frecuencia teórica en alguna clase es menor que 5, \(  np_{i}<5 \), entonces dicha clase se agrupará con otras clases contiguas de manera que en todas ellas dichas frecuencias sean mayores o iguales a 5 reduciéndose el número de clases y como consecuencia el número de grados de libertad.

Ejemplo 11.1: Se realizan uno estudios para medir el número de partículas, procedentes de una sustancia radiactiva, que llegan a una determinada zona en un corto espacio de tiempo siempre igual. Los resultados se muestran en la siguiente tabla

 \(  \begin{array}{| l| c|c|c|c|c|c|c|} \hline  N^{o} \hspace {.2cm} de \hspace {.2cm} partículas &   0  &  1  &  2  &  3 &   4  &   5 &   6 \\ \hline  N^{o} \hspace {.2cm} de \hspace {.2cm} periodos \hspace {.2cm} de \hspace {.2cm} tiempo  &  269  &  325  &  207  &  82 &    28   &  7  &  2 \\ \hline \end{array}  \)

Se pide:

a) Ajustar una distribución de Poisson

b) Calcular la probabilidad de que lleguen a dicha superficie: 0 partículas; 3 partículas; por lo menos 3 partículas; más de 3 partículas; menos de 3 partículas

c) Verificar la bondad de ajuste mediante un contraste de la  \(  χ^{2}  \).

Respuesta: Sea \( X \): “Número de partículas radiactivas”

a) La distribución de Poisson está caracterizada por el parámetro \( λ \), dicho parámetro es desconocido por ello lo estimamos a partir de la muestra

\( λ= \overline {x} = \displaystyle \frac { 1} {n} \displaystyle \sum_{i=1}^{7} n_{i}x_{i}= \displaystyle \frac {0 \times 269+1 \times 325+ \cdots +6 \times 2} {269+325+ \cdots +2}=1.24 \Rightarrow   X \rightarrow  P(λ=1.24) \)

b) \( P[X=s]=e^{-λ} \displaystyle \frac {λ^{s}}{s!} \)

\( P(X=0)=e^{-1.24} \displaystyle \frac {λ^{0}}{0!}=0.2894  \hspace{4cm} \) \( P(X=3)=e^{-1.24}\displaystyle \frac {λ^{3}}{3!}=0.0919 \) \(  \begin{array}{l c} \\ P(X \geq 3) & =  1-P(X<3)=1-P(X=0)-P(X=1)-P(X=2) = \\ & =  1-0.2898-0.3588-0.2224=0.129 \\  \end{array}  \) \(  \begin{array}{l c} \\ P(X>3) & =  1-P(X \leq 3)=1-P(X=0)-P(X=1)-P(X=2)-P(X=3) = \\ & =1-0.2898-0.3588-0.2224-0.0919 = 0.0371 \\  \end{array} \)

 

\( P(X<3)=P(X=0)+P(X=1)+P(X=2)=0.871 \)

c) Contraste de bondad de ajuste

\(  \left.  \begin{array} \\  H_0 \equiv  X  \rightarrow P(λ=1.24)   \\  H_1 \equiv  X \hspace {.2cm} sigue \hspace {.2cm} otra \hspace {.2cm} distribución   \\ \end{array} \right \} \rightarrow   \left \{  \begin{array} \\    χ_{exp}^{2}=  \displaystyle \sum_{i=1}^{k} \displaystyle \frac{  (n_{i}-np_{i})^{2}} {np_{i}} \\  Si \hspace {.2cm} χ_{exp}^{2} \geq χ_{α;k-r-1}^{2}      \Rightarrow  \hspace {.2cm} Se \hspace {.2cm} rechaza \hspace {.2cm}  H_0   \\ \end{array} \right. \)

\(  \begin{array}{| c| c|c|c|} \hline  Nº \hspace {.2cm} de \hspace {.2cm} partículas  &  Fre. \hspace{ .2cm} absolutas &  Probabilidades & Valores \hspace{ .2cm}  esperados   \\     &       empíricas \hspace{ .2cm} n_{i}   & teóricas \hspace{ .2cm} p_{i} & np_i \\   \hline 0 &   269  &  0.2894  &  266.248  \\ \hline 1  &  325  &  0.3588 &   330.096 \\ \hline 2  &  207 &   0.2224 &   204.608  \\ \hline  3 &   82  &  0.0919 &   84.548  \\ \hline 4  &  28 &   0.0285 &   26.22 \\ \hline 5  &  7  &  0.0070  &  6.44 \\ \hline 6  &  2  &  0.0014  &  1.288  \\ \hline  &  n=920  &  1  &  919.448 \\ \hline \end{array}  \)

   Al ser el último valor esperado menor que 5 unimos las dos clases contiguas

\(  \begin{array}{| c| c|c|c|c|} \hline  Nº \hspace {.2cm} de \hspace {.2cm} partículas  &  n_i &  p_i & np_i     &  \displaystyle \frac {(n_i – np_i)^{2}}{np_i} \\   \hline 0 &   269  &  0.2894  &  266.248 &  0.0284  \\ \hline 1  &  325  &  0.3588 &   330.096 & 0.0786  \\ \hline 2  &  207 &   0.2224 &   204.608  & 0.0280 \\ \hline  3 &   82  &  0.0919 &   84.548 & 0.0767  \\ \hline 4  &  28 &   0.0285 &   26.22 & 0.1208 \\ \hline 5  &  9  &  0.0084  &  7.728  &  0.2093  \\ \hline  &  n=920  &  1  &  919.448 & 0.5418 \\ \hline \end{array}  \)

\( \displaystyle \sum_{i=1}^{k} \displaystyle \frac {(n_{i}-np_{i})^{2}} {np_{i}}  \rightarrow  χ_{k-r-1}^{2} \)

k: Número de clases; k=6

r: Número de parámetros estimados; r=1

\( χ_{exp}^{2}=\displaystyle \sum_{i=1}^{k} \displaystyle \frac {(n_{i}-np_{i})^{2}} {np_{i}} =0.5418 \)

\(  χ_{α;k-r-1}^{2}=χ_{0.05;6-1-1}^{2}=χ_{0.05;4}^{2}=9.49> χ_{exp}^{2}\rightarrow  \) No se rechaza \( H_{0} \)

Los datos provienen de una distribución de Poisson

Ejemplo 11.2: Se ha observado el número de hijos varones en 1000 familias, cada una de ellas con 5 hijos, obteniéndose los siguientes resultados:

\(  \begin{array}{| l| c|c|c|c|c|c|} \hline  N^{o} \hspace{ .2cm} de \hspace{ .2cm} hijos \hspace{ .2cm} varones &   0  &  1 &   2  &  3 &   4  &  5 \\ \hline N^{o} \hspace{ .2cm} de \hspace{ .2cm} familias  &  31  &  168 &   319 &   308  &  150  &  24 \\ \hline \end{array}  \)

Ajustar una distribución binomial y estudiar la bondad del ajuste.

Respuesta:

Sea la variable aleatoria \( X \) que representa el número de hijos varones en una familia,  \(  X \rightarrow B(5, p) \). El parámtero \( p \) es desconocido y tenemos que estimarlo con base en la información suministrada por la muestra, así determinamos la probabilidad \(  p \) a partir de la media muestral: \(  \overline {x} =5p \)

\(  \overline {x} = \displaystyle \frac { 31 \times 0+168 \times 1+ \cdots + 24 \times 5 } {1000}=2.455 \Rightarrow p= \displaystyle \frac { 2.455 } {5}=0.49 \)

Hallamos las probabilidades teóricas o esperadas a partir de la función de probabilidad de la distribución binomial

\(  P[X=r]= { 5 \choose r } (0.49)^{r}(0.51)^{5-r} \)

\(  \begin{array}{| c| c|c|c|} \hline  Nº \hspace {.2cm} hijos \hspace {.2cm} varones  &  Fre. \hspace{ .2cm} absolutas &  Probabilidades & Fre. \hspace{ .2cm} absolutas    \\     &       empíricas \hspace{ .2cm} n_{i}   & teóricas \hspace{ .2cm} p_{i} &  teóricas  \hspace{ .2cm} np_i \\   \hline 0   &  31 &   0.0345 &   34.5 \\ \hline 1  &  168  &  0.1657  &  165.7 \\ \hline 2  &  319  &  0.3185  &  318.5 \\ \hline  3  &  308  &  0.3060  &  306.0 \\ \hline 4   & 150  &  0.1470  &  147.0 \\ \hline 5  &  24  &  0.0283  &  28.3 \\  \hline   \end{array}  \)

y el siguiente valor para el estadístico de contraste

\( χ_{exp}^{2}=\displaystyle \sum_{i=1}^{k} \displaystyle \frac {(n_{i}-np_{i})^{2}} {np_{i}} = \displaystyle \frac {(31-34.5)^{2}} {34.5}+ \displaystyle \frac {(168-165.7)^{2}}{165.7}+ \cdots + \displaystyle \frac {(24-28.3)^{2}}{28.3}=1.115 \)

el número de grados de libertad es: 6-1-1=4. Para un nivel de significación del 5%  \( χ_{0.05;4}^{2}=9.49>χ_{exp}^{2} \Rightarrow \)  No se rechaza \( H_0 \Rightarrow \) se puede afirmar que el ajuste es bueno.

Ejemplo 11.3. En una factoría de automóviles se ha observado la duración de las baterías de 40 coches, obteniéndose la siguiente tabla

\(  \begin{array}{| c| c|} \hline  Límites \hspace {.2cm}  de \hspace {.2cm}  clase   &  Fre.  \hspace {.2cm}  absolutas   \\   \hline  1.45-1.95  &   2 \\   \hline  1.95-2.45  &   1 \\ \hline  2.45-2.95 &   4 \\ \hline 2.95-3.45  &   15 \\ \hline   3.45-3.95  &  10 \\ \hline  3.95-4.45 &   5 \\ \hline  4.45-4.95  &  3 \\  \hline   \end{array}  \)

Comprobar la hipótesis de que la distribución de frecuencias de las duraciones de la baterías, dadas en la tabla anterior, se puede aproximar mediante una distribución Normal de media μ=3.5 y desviación típica σ=0.7.

Respuesta:

\(  \begin{array}{| c| c c|c|c c|} \hline  Clases  &  Fre. \hspace{ .2cm} absolutas & &  Probabilidades & Fre. \hspace{ .2cm} absolutas &   \\     &       empíricas \hspace{ .2cm} n_{i}   & & teóricas \hspace{ .2cm} p_{i} &  teóricas  \hspace{ .2cm} np_i  &\\   \hline   1.45-1.95 &  2 & &   0.012 & 0.5 & \\  1.95-2.45  &  1 & 7  &  0.0525  &  2.1 & 8.5 \\  2.45-2.95  &  4  & &  0.1475  &  5.9 & \\   2.95-3.45  &  15 &  &  0.2573  &  10.3 & \\  3.45-3.95   & 10 & &  0.2674  &  10.7 & \\  3.95-4.45  &  5 & 8 &  0.175  &  7.0 & 10.5 \\   4.45-4.95 & 3 & & 0.0874 & 3.5 & \\  \hline  \end{array}  \)

Las probabilidades teóricas se obtienen de la siguiente forma:

\(  \begin{array}{l c} \\  P[1.45\leq x \leq 1.95] & =P \left [  \displaystyle \frac { 1.45-3.5}{0.7} \leq z \leq \displaystyle \frac {1.95-3.5} {0.7} \right ]=P[-2.93 \leq z \leq -2.21]= \\ & = P[z \geq 2.21]-P[z \geq 2.93]=0.0136-0.00169=0.012 \\  \end{array} \)

Nótese que, en la tabla anterior, hemos agrupado clases contiguas donde las frecuencias teóricas son menores que 5, \( np_{i}<5 \), de manera que en todas las clases dichas frecuencias sean mayores o iguales a 5. En consecuencia, el número total de intervalos se reduce de 7 a 4 y por lo tanto el número de grados de libertad es 4-1=3. El valor del estadístico de contraste es:

\( χ_{exp}^{2}= \displaystyle \sum_{i=1}^{4} \displaystyle \frac { (n_{i}-np_{i})^{2}}{np_{i}}= \displaystyle \frac {(7-8.5)^{2}}{8.5}+ \displaystyle \frac {(15-10.3)^{2}}{10.3}+ \displaystyle \frac {(10-10.7)^{2}}{10.7}+ \displaystyle \frac {(8-10.5)^{2}}{10.5}=3.05 \)

Para un nivel de significación del 5%; \( χ_{0.05;3}^{2}=7.815>χ_{exp}^{2} \Rightarrow \) No hay razón para rechazar \( H_0  \) y se concluye que la distribución N(3.5; 0.7) proporciona un buen el ajuste de las duraciones de las baterías.

Contrastes para la independencia de dos caracteres

En este capítulo y capítulos anteriores hemos considerado el estudio de un único carácter en una o dos poblaciones, sin embargo un problema muy interesante, en las ciencias experimentales, es estudiar conjuntamente dos caracteres en una misma población, en donde cada carácter puede presentar dos o más modalidades diferentes y preguntarse si existe o no algún tipo de relación entre ambos caracteres. El procedimiento estadístico que se utiliza en tal situación está, en parte, determinado por la naturaleza de las variables que intervienen. Si las dos variables son cualitativas, el modo de determinar si están relacionadas es mediante los Contrastes de Independencia de dos Caracteres que estudiamos en esta sección y el procedimiento de la prueba de la \( χ^{2} \) que se presentó en la sección anterior también puede utilizarse para resolver estos contrastes.

Por ejemplo, ¿existe relación entre el color de la piel y el color del pelo? o ¿existe relación entre fumar cigarrillos y la predisposición a desarrollar cáncer de pulmón? En ambos ejemplos, se ha clasificado a la población en dos caracteres y se supone que cada uno de estos caracteres presentan por lo menos dos modalidades exhaustivas y mutuamente excluyentes. Así,

• En el primer ejemplo los dos caracteres son el color de la piel y el color del pelo y las modalidades de estos dos caracteres podrían ser oscura y clara, para el primer carácter, y negro, rubio y pelirrojo para el segundo.
• En el segundo ejemplo los dos caracteres son si es fumador, y si desarrolla cáncer de pulmón y las modalidades de estos dos caracteres podrían ser: no-fumador, moderado y crónico, para el primer carácter, y si desarrolla  o no cáncer de pulmón para el segundo.

En una prueba de independencia el único número que el investigador controla directamente es el tamaño total de la muestra. Se extrae una muestra de tamaño n de la población y cada dato se clasifica según las dos variables que se estudian. Ni las frecuencias de cada celda ni los totales de fila y columna se conocen de antemano.

Las frecuencias observadas en cada una de las modalidades de los caracteres se presentan en la Tabla 11.1, que se conoce como una Tabla de Contingencia con dos criterios de clasificación.

De un modo general, los n individuos de una muestra aleatoria se clasifican de acuerdo con dos caracteres cualitativos A y B, cada uno de los cuales admite r y s modalidades diferentes, respectivamente, constituyendo una tabla de contingencia con r filas y s columnas, que se le conoce como una tabla r×s y se muestra a continuación

\(  \begin{array}{| c| c| c|c|c| c|c|c|} \hline  A/B &   B_1  &  B_2 &  \cdots  &  B_{j} &   \cdots &  B_{s} &   Totales \\   \hline A_1 &    n_{11} &    n_{12} &   \cdots  &  n_{1j} & \cdots &    n_{1s} &   n_{1.} \\ A_2 &    n_{21} &    n_{22} &   \cdots  &  n_{2j} & \cdots &    n_{2s} &   n_{2.} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ A_i &    n_{i1} &    n_{i2} &   \cdots  &  n_{ij} & \cdots &    n_{is} &   n_{i.} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ A_r &    n_{r1} &    n_{r2} &   \cdots  &  n_{rj} & \cdots &    n_{rs} &   n_{r.} \\  \hline  Totales  &   n_{.1} &   n_{.2} & \cdots &    n_{.j} & \cdots &   n_{.s} &   n \\  \hline  \end{array}  \)

Tabla 11.1: Tabla de contingencia

Donde hemos denotado por:

• \( A_1, A_2, \cdots , A_{r} \) cada una de las modalidades del carácter \( A \)
• \( B_1, B_2, \cdots , B_{s} \) cada una de las modalidades del carácter \( B \)
• \( n_{ij} \) la frecuencia absoluta observada en las modalidades \( (i, j) \) de los caracteres \( A \) y \( B \), respectivamente, con \( i=1, 2, \cdots , r \) y \( j=1, 2, \cdots, s \)
• \(  n_{i.}= \displaystyle \sum_{i=1}^{r}n_{ij}\) es el total de la i-ésima fila
• \( n_{.j}= \displaystyle \sum_{j=1}^{s}n_{ij} \) es el total de la j-ésima columna
• \( n= \displaystyle \sum_{i=1}^{r}\displaystyle \sum_{j=1}^{s}n_{ij} \) es el total general

La decisión de no rechazar o rechazar la hipótesis nula de independencia de los dos caracteres se basa en el buen o mal ajuste de las frecuencias observadas en cada una de las celdas de la tabla de contingencia y las frecuencias que se esperarían para cada celda bajo la suposición de que \( H_0 \) es cierta, siendo \( H_0 \)

\( H_0 \equiv \) Los caracteres A y B son independientes.

Las frecuencias esperadas de cualquier celda se obtienen mediante la siguiente fórmula

\(  Frecuencia \hspace{ .2cm} esperada = \displaystyle \frac {(Total \hspace{ .2cm} de \hspace{ .2cm} la \hspace{ .2cm} columna) \times (Total \hspace{ .2cm} de \hspace{ .2cm} la \hspace{ .2cm} fila) } {Total general} \)

Si denotamos las frecuencias teóricas por \(  e_{ij} \), la expresión anterior se puede poner de la siguiente forma

\(  e_{ij}= \displaystyle \frac {n_{i.}n_{.j}}{n} \)

Se define el siguiente estadístico de contraste

\(   χ^{2}= \displaystyle \sum_{i=1}^{r} \displaystyle \sum_{j=1}^{s} \displaystyle \frac {(n_{ij}-e_{ij})^{2}}{e_{ij}} \)

que, bajo la hipótesis nula, se aproxima a una distribución \( χ^{2} \)  con \(  (r-1) \times (s-1) \) grados de libertad, si \(  e_{ij}>5 \).

Si algún valor de las frecuencias teóricas o esperadas, \( e_{ij}\), es menor que 5 en lugar de agrupar filas o columnas contiguas debido al problema que puede presentar, se aplica una corrección que recibe el nombre de Corrección de Yates para continuidad, que consiste en restar 0.5 a cada una de las diferencias entre las frecuencias observadas y las teóricas, dando lugar al siguiente estadístico de contraste.

\(  χ²(corregido)= \displaystyle \sum_{i=1}^{r}\displaystyle \sum_{j=1}^{s} \displaystyle \frac {||n_{ij}-e_{ij}|-0.5)^{2}}{e_{ij}} \)

Si las frecuencias esperadas, \( e_{ij} \), son grandes, los valores de los estadísticos de contrastes corregidos y sin corregir son casi los mismos.

Ejemplo 11.4. Durante un periodo de tiempo se llevó a cabo un estudio médico, para determinar, si los hábitos de un fumador pueden influir en el desarrollo del cáncer de pulmón. Los resultados obtenidos se muestran en la siguiente tabla

\(  \begin{array}{| c| c|c|c|} \hline  Enfermedad / Fumador  &  No-Fumador  &  Moderado &   Crónico  \\   \hline   SI &   350  &  1200  &  1450  \\  \hline  NO  &   525 &   900 &   575   \\  \hline  \end{array}  \)

Razonar con una significación del 5% si el hecho de desarrollar cáncer pulmonar está relacionado con el hábito de fumar.

Respuesta:

\(  \begin{array}{| c| c|c|c|c|} \hline  Enfermedad / Fumador  &  No-Fumador  &  Moderado &   Crónico & \\   \hline   SI &   350  &  1200  &  1450 & 3000 \\  \hline  NO  &   525 &   900 &   575 & 2000  \\  \hline & 875  &  2100  &  2025  &  5000 \\  \hline  \end{array}  \)

\(  \begin{array}{| c| c|c|c|} \hline  e_{ij}  &  No-Fumador  &  Moderado &   Crónico  \\   \hline   SI  &  525 &   1260  &  1215  \\  \hline  NO  &  350  &  840 &   810  \\  \hline  \end{array}  \)

\(  \begin{array}{| c| c|c|c|} \hline  \displaystyle \frac { (n_{ij}-e_{ij})^{2}} {e_{ij}} &  No-Fumador  &  Moderado &   Crónico  \\   \hline   SI  &  58.3  &  2.8571  &  45.4526 \\  \hline  NO  &  87.5  &  4.2857  &  68.1790 \\  \hline  \end{array}  \)

\(  \left.  \begin{array} \\  H_0 \equiv  Independencia  \\  H_1 \equiv  No-independencia \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\ χ_{exp}^{2}= \displaystyle \sum_{i=1}^{2}\displaystyle \sum_{j=1}^{3} \displaystyle \frac { (n_{ij}-e_{ij})^{2}} {e_{ij}} =266.6077  \\  χ_{teórica}^{2}=χ_{α;(r-1)(s-1)}^{2}=χ_{0.05;2}^{2}=5.9915 \end{array} \right. \)

Como \( χ_{exp}^{2} > χ_{teórica}^{2}\Rightarrow  \) Se rechaza \( H_0 \). Por lo tanto no hay independencia entre los caracteres.

Contrastes de homogeneidad

El problema general es determinar si varias muestras cualitativas se pueden considerar procedentes de una misma población en cuyo caso decimos que las muestras son homogéneas.

Ejemplos de problemas de homogeneidad se pueden plantear en términos de comprobar si varios tratamientos, que curan una misma enfermedad, aplicados a un cierto tipo de enfermos son homogéneos respecto a los resultados obtenidos. Si únicamente consideramos dos tratamientos A y B y los aplicamos a dos muestras independientes de individuos anotando cuantos de dichos individuos se curan y cuantos no. El problema consiste en comparar dos proporciones de curados una de cada tratamiento que se estudió en el Capítulo 10. Pero si en lugar de clasificar los resultados en números de individuos que se curan o no, clasificamos dichos resultados en más de dos categorías, por ejemplo “Peor”, “Igual” y “Mejor”, o si consideramos más de dos tratamientos, el problema que se plantea es contrastar que todos los tratamientos son igualmente de efectivos, es decir que la proporción de individuos que empeoran, permanecen igual o que mejoran es la misma en todos los tratamientos y este problema el que vamos a resolver en esta sección.

En los contrastes de independencia, considerados en la sección anterior, estábamos interesados en saber si, en los individuos de una misma población, dos caracteres estaban relacionados, en estos contrastes el único número que el investigador controla directamente es el tamaño de total de la muestra. Un contraste de homogeneidad proporciona otra aproximación al problema. Ahora en lugar de realizar una prueba de independencia, se prueba la hipótesis de que las proporciones poblacionales dentro de cada fila son las mismas. Esto es, en el Ejemplo 11.4 se probaría la hipótesis de que las proporciones de individuos “No-fumadores”, “moderados” y “crónicos” que tienen la enfermedad son las mismas que las proporciones de individuos de cada categoría que no tienen la enfermedad. En esencia interesa probar si las tres categorías de hábitos de fumador son homogéneas con respecto a tener o no la enfermedad. Por lo tanto, un contraste de homogeneidad contrasta una hipótesis nula que afirma que diferentes poblaciones son homogéneas con respecto a alguna característica de interés, contra una hipótesis alternativa que asegura que no lo son.

En una prueba de homogeneidad un conjunto de marginales totales está fijado por el investigador, mientras que el otro es aleatorio. Por ejemplo, queremos saber si hay algún tipo de asociación entre la exposición a radiactividad y el desarrollo de una cierta enfermedad, para llevar a cabo el experimento se eligen muestras aleatorias de 300 personas que han estado expuestas a la radiación y 320 que no han estado expuestas. En este caso, los totales de filas marginales se han fijado en 300 y 320, estos tamaños de muestras son determinados previamente por el investigador. Los totales de columnas marginales son libres, son variables aleatorias cuyos valores numéricos se conocen al final del experimento. Si no hay asociación entre la exposición a radiactividad y el desarrollo de la enfermedad, la proporción de personas con la enfermedad debería ser la misma en las dos poblaciones. Si hay asociación, estas proporciones podrían ser distintas.

Los contrastes de homogeneidad conllevan tablas que son similares a las tablas de contingencia, en efecto, el procedimiento para llevar a cabo tales contrastes es exactamente el mismo que el utilizado en el test de la \(  χ^{2} \) en unión con las tablas de contingencia. Ilustramos este procedimiento en el siguiente ejemplo:

Ejemplo 11.5. Un grupo de personas han estado expuestas a la radiactividad procedente de un vertedero en el que se almacenan desechos atómicos. Se realiza una investigación para descubrir si hay alguna asociación entre la exposición y el desarrollo de una cierta enfermedad en la sangre. Para llevar a cabo el experimento se eligen muestras  aleatorias de 300 personas de la comunidad que han estado expuestas al peligro y 320 no expuestas ¿Qué se puede concluir a la vista de los resultados?

\(  \begin{array}{| c| c|c|c|} \hline  Expuestos/Radiactividad  &  SI  &  NO  &  Total  \\   \hline   SI  &  52 &   248 &   300  \\  \hline  NO  &   48  &  272 &   320  \\  \hline Total  &  100  &  520  &  620 \\  \hline  \end{array}  \)

Respuesta:

\( H_0 \equiv \)  Proporción de personas con la enfermedad de los expuestos a la radiactividad = Proporción de personas con la enfermedad (no expuestos a la radiactividad)

\(  \begin{array}{| c| c|c|} \hline  e_{ij}= \displaystyle \frac {  n_{i.}n_{.j} } {n} &    SI  &  NO \\   \hline   SI  &  48.39  &  251.61 \\  \hline  NO  &  51.61 &   268.39 \\  \hline  \end{array}  \)

\(  \begin{array}{| c| c|c|} \hline  \displaystyle \frac { (n_{ij}-e_{ij})^{2}} {e_{ij}} &  SI &  NO  \\   \hline   SI &   0.2693  &  0.0518  \\  \hline  NO &   0.2525  &  0.0485  \\  \hline  \end{array}  \)

\(  \left.  \begin{array} \\  H_0 \equiv  Las \hspace{.2cm} poblaciones \hspace{.2cm}  son \hspace{.2cm}  homogéneas \\  H_1 \equiv  Las \hspace{.2cm} poblaciones \hspace{.2cm} no \hspace{.2cm}  son \hspace{.2cm}  homogéneas \\ \end{array} \right \} \rightarrow  \left \{  \begin{array} \\ χ_{exp}^{2}= \displaystyle \sum_{i=1}^{3}\displaystyle \sum_{j=1}^{2} \displaystyle \frac { (n_{ij}-e_{ij})^{2}} {e_{ij}} =0.6221 \\  χ_{teórica}^{2}=χ_{α;(r-1)(s-1)}^{2}=χ_{0.05;1}^{2}=3.48 \end{array} \right. \)

Como \( χ_{exp}^{2} < χ_{teórica}^{2}\Rightarrow  \) No se rechaza \( H_0 \). Por lo tanto hay evidencia de asociación entre la exposición a esta fuente de radiactividad y el desarrollo de esta enfermedad en la sangre.

Ejercicios propuestos: Relación XI

1. A lo largo de 540 días se anota el número de accidentes mortales de tráfico que se producen en una ciudad, obteniéndose los resultados de la tabla adjunta.

\(  \begin{array}{| c| c|c|c|c|c|c|} \hline  N^{o} \hspace{.2cm} de \hspace{.2cm} accidentes \hspace{.2cm} mortales \hspace{.2cm} por  \hspace{.2cm} día   & 0 &   1  &  2  &  3  &  4  &  5  \\   \hline   N^{o} \hspace{.2cm} de \hspace{.2cm} días  &  132 &   195  &  120  &  60 &   24  &  9  \\  \hline  \end{array}  \)

Se pide:

a) ¿Qué distribución podremos ajustar y por qué?(Solución: Poisson)

b) Estudiar la bondad del ajuste. (Solución:  \(  χ_{exp}^{2}=3.109 \))

c) ¿Cuántos días se producirán dos accidentes mortales en un año? (Solución: 88 días).

2. Una central de transformación de productos lácteos produce un preparado para niños en edad de lactancia. Se analiza el contenido de materia grasa de los mismos. Para ello se utiliza una muestra de 742 preparados y los resultados agrupados en 8 clases están expresados en la tabla adjunta.

Se pide:

a) ¿Se puede admitir que el contenido de materia grasa se distribuye normalmente?(Solución: N(0.39; 0.042))

b) Contrastar la bondad del ajuste mediante la  \( χ^{2} \). (Solución: \(  χ_{exp}^{2}=25.8022 \)).

\(  \begin{array}{| c| c|} \hline  0.255-0.285 &   6  \\     0.285-0.315  &  38 \\ 0.315-0.345  &  66 \\ 0.345-0.375  &  131 \\ 0.375-0.405  &   240 \\ 0.405-0.435  &  162 \\ 0.435-0.465  &  84 \\ 0.465-0.495  &  15  \\  \hline  \end{array}  \)

3. Tomamos una muestra de 650 análisis de sangre realizados en un laboratorio clínico y  anotamos el número de eritrocitos por milímetro cúbico de sangre. Los resultados agrupados en 7 clases son los que figuran en la tabla adjunta.

Se pide:

a) ¿Se puede admitir que el nº de eritrocitos se distribuyen normalmente? (Solución: Si se puede admitir)

b) Calcular la probabilidad de que el número de eritrocitos en millones, esté comprendido entre 4.5 y 5.5. (Solución: 0.3208).

\(  \begin{array}{| c| c|} \hline  N^{o} \hspace{.2cm} de \hspace{.2cm} eritrocitos   &  N^{o} \hspace{.2cm} de \hspace{.2cm} días \\ en millones &  \\   \hline     menos  \hspace{.2cm} de  \hspace{.2cm} 2.5 &   8 \\  2.5-3.5 &   52 \\ 3.5-4.5   &  140 \\ 4.5-5.5 &   210 \\ 5.5-6.5  &  160 \\ 6.5-7.5  &  70 \\ 7.5  \hspace{.2cm} y  \hspace{.2cm} más  &  10 \\  \hline  \end{array}  \)

4. Se realiza una investigación para determinar si hay alguna asociación entre el peso de un estudiante y un éxito precoz en la escuela. Se selecciona una muestra de 500 estudiantes y se clasifica a cada uno según dos criterios, el peso y el éxito en la escuela. Los datos se muestran en la tabla adjunta. (Solución: \(  χ_{exp}^{2}=4.18 \); La obesidad y precocidad en la escuela no son independientes)

\(  \begin{array}{| c| c|c|} \hline  Éxito/Sobrepeso  &  SI  &  NO \\   \hline     SI   & 162  &  263 \\  \hline NO &   38 &   37 \\  \hline  \end{array}  \)

5. En 5 zonas de la provincia de Granada (Ladihonda y Fazares, zonas muy secas y Cortijuela, Molinillo y Fardes, zonas húmedas) se hacen una serie de mediciones de la longitud de las hojas de las encinas a lo largo de 3 años consecutivos: 1995, muy seco y 1996 y 1997, muy lluviosos. Los datos se muestran a continuación ¿Se puede admitir que la longitud de las hojas de encina se distribuye normalmente?
Longitud: 26,51; 30,17; 34,24; 31,04; 34,99; 30,48; 25,07; 25,04; 29,16; 35,12; 25,41; 27,02; 23,04; 27,69; 34,71 (Solución: La longitud de las hojas sigue una distribución Normal).

6. Tiramos un dado 720 veces y obtenemos los siguientes resultados. Contrástese la hipótesis de que el dado está bien construido al nivel de significación α=0.01. (Sol: \(  χ_{exp}^{2}=0.683 \); Si está bien construido)

\(  \begin{array}{| c| cccccc|} \hline  x_{i} &   1  &  2  &  3  &  4 &   5  &  6  \\   \hline     n_{i}  &  116  &  120   &  115 &   120 &   125 &   124  \\  \hline  \end{array}  \)

7. Para comprobar las leyes de Mendel, cruzamos guisantes obteniendo los siguientes resultados

\(  \begin{array}{| c| cccc|} \hline  & amarillos  &  amarillos  &   verdes  &  verdes \\   & lisos &   rugosos  &  lisos &   rugosos  \\ \hline    N^{o} \hspace{.2cm} de \hspace{.2cm} guisantes  &  262  &  91  &  86  &  31 \\  \hline  \end{array}  \)

Las proporciones esperadas son: 9, 3, 3, 1.

¿Contradicen estos resultados obtenidos las proporciones esperadas? Estúdiese al nivel de significación del 1%. (Sol: \(  χ_{exp}^{2}=0.498 \). No los contradice).

8. Se realiza un estudio para investigar el efecto de la presencia de una gran planta industrial sobre la población de invertebrados en un río que atraviesa la planta. Se tomaron muestras de siete especies de invertebrados en dos zonas del río: antes de la planta “Aguas arriba” y después de la planta “Aguas abajo”. Los datos se muestran en la siguiente tabla

\(  \begin{array}{| c| ccccccc|} \hline  Zonas  &  A  &  B &   C &   D  &  E  &  F &   G  \\ \hline    Aguas \hspace{.2cm} arriba  &  37  &  12  &  10  &  18  &  11  &  16  &  59 \\  Aguas \hspace{.2cm} abajo  &  19  &  10  &  7  &  20 &   8  &  12 &   24  \\  \hline  \end{array}  \)

Se pide:

a) ¿Se puede admitir que el tipo de especies de vertebrados está relacionado con la situación respecto de la planta de “Aguas arriba del río”? (Solución: el tipo de especies de vertebrados está relacionado con la situación respecto de la planta de “Aguas arriba del río”)

b) ¿Se puede admitir relación entre la situación respecto a la planta de la zona del río y el tipo de especies halladas en ella? (Solución: la situación respecto a la planta de las dos zonas del río es independiente del tipo de especies halladas en ellas).

9. Ante una epidemia se desea contrastar si padecer la enfermedad es independiente de una vacunación previa. Para ello, se toma una muestra de 300 personas y se obtuvieron los siguientes resultados. (Sol:  \(  χ_{exp}^{2}=2.257<χ_{α}^{2} =3.84 \). Si son independientes)

\(  \begin{array}{| c| c|c|c|} \hline  Vacunados/Enfermos  &  SI  &  NO &   Total \\ \hline    SI  &  40 &   110  &  150 \\  \hline NO  &  52  &  98  &  150 \\ \hline   Total  &  92  &  208 &   300   \\  \hline  \end{array}  \)

10. Los resultados de una encuesta realizada con el fin de determinar, si la edad de los individuos influye a la hora de contraer una determinada enfermedad, fueron los dados en la tabla adjunta. ¿Se puede admitir la hipótesis de que el número de individuos que contraen la enfermedad, es independiente de la edad? (Sol: \(  χ_{exp}^{2} =29.316>χ_{α}^{2}=9.4 \)  No).

\(  \begin{array}{| c| c|c|} \hline  & Contraen   & Contraen \\ & la \hspace{.2cm} enfermedad  & la \hspace{.2cm} enfermedad   \\ \hline       EDAD  &  SI  &   NO \\  \hline menos \hspace{.2cm} de \hspace{.2cm} 15 \hspace{.2cm} años  &  38 &   44  \\ \hline   15-30  &  45 &   28 \\  \hline 30-45  &  30  &  54 \\ \hline 45-60 &   22 &   62 \\ \hline más \hspace{.2cm} de \hspace{.2cm} 60 \hspace{.2cm} años  &  20  &  57  \\ \hline   Total  &  155  &  245 \\ \hline    \end{array}  \)

11. A la mitad de los 160 enfermos de un hospital se les somete a un determinado tratamiento adicional T, contabilizándose al cabo de un cierto tiempo que entre estos se han recuperado 63, mientras que de los no tratados solamente se han recuperado 57. Contrástese la hipótesis de que la curación es independiente de la aplicación del tratamiento T, al nivel de significación α=0.05. (Sol: \(   χ_{exp}^{2}=1.2 \). Si son independientes.)

12. Contrástese la hipótesis H₀ de que la proporción de estudiantes suspendidos en Bioestadística por los 4 profesores de dicha asignatura fue la misma, para un nivel de significación del 5%, si una vez entregadas las actas los resultados fueron los dados en la tabla adjunta. (Sol: \(   χ_{exp}^{2}=2.928 \), No se rechaza \(   H_0 \)).

\(  \begin{array}{| c| c|c|c|c|c|} \hline  & Prof. A &   Prof. B  &  Prof. C &   Prof. D  &  Total  \\ \hline    APROBADOS  &  150  &  141  &  168  &  152  &  611  \\  \hline SUSPENSOS  &  30 &   40  &  32  &  37 &   139  \\ \hline   Total  &  180 &   181  &  200  &  189 &   750   \\  \hline  \end{array}  \)

13. La observación de 302 individuos procedentes de la segunda generación de pares de raza pura diferenciados por dos pares de caracteres alelomorfos AALL, VVRR, en los que los caracteres A y L son dominantes, han dado los resultados que figuran en la tabla adjunta. ¿Se puede considerar que el crecimiento ha seguido las leyes de Mendel con un nivel de confianza del 95%? (Sol: \(  χ_{exp}^{2} =1.50 \). Si se puede considerar). aqui

\(  \begin{array}{| c| c|c|c|} \hline  & FENOTIPO  &  FENOTIPO  &  FENOTIPO   &  FENOTIPO \\ \hline    & AL &   VL  &  AR  &  VR \\  \hline   N^{o} \hspace{.2cm} individuos  &  161 &   61  &  63  &  17   \\  \hline  \end{array}  \)

14. El rendimiento de la cosecha de un cereal se considera: muy bueno, si la producción es superior a 25 Kgrs. por área de cultivo, bueno si es superior a 15 Kgrs. y malo si no llega a 15 Kgrs. Se hacen 30 determinaciones del rendimiento en otras tantas parcelas donde se ha sembrado cereal de tipo A, y 30 determinaciones en parcelas donde se sembró un cereal de tipo B. Los resultados son los dados en la tabla adjunta. ¿Son igualmente efectivos para el cultivo los dos tipos de cereales A y B? (Sol: \(  χ_{exp}^{2}=1.134 \). Si son igualmente de efectivos)

\(  \begin{array}{| c| c|c|} \hline  Rendimiento/Tipo \hspace{.2cm}  cereal  &  A  &  B \\ \hline    MUY \hspace{.2cm} BUENO &   10  &  12  \\  \hline BUENO  &  14 &   10  \\ \hline   MALO &   6 &   8 \\  \hline  \end{array}  \)

15. En la tabla adjunta se reflejan las notas de Bioestadística y Fisiología de una muestra de 100 alumnos. Para un nivel de significación α=0.01, ¿Son independientes las calificaciones obtenidas en ambas asignaturas? (Sol:  \(  χ_{exp}^{2}=26.915 \). Si son independientes).

\(  \begin{array}{| c| ccccc|} \hline   & &  & Bioestadística &   &  \\ \hline     & & Sobres.  &  Notable  &  Aprobad.  &  Suspenso  \\ \hline   & Sobres.  &  10  &  6 &   4  &  4 \\  \hline Fisiología  &   Notable  &   6  &   4   &  8  &  6 \\ \hline & Aprobado &   4  &  18 &   3 &   4 \\ \hline  & Suspenso &   6  &   2  &   6  &   9  \\ \hline   \end{array}  \)

16. Para curar una cierta enfermedad, se sabe que existen 5 tratamientos diferentes. Aplicados por separado, cada uno, a un grupo de enfermos que padecen esa enfermedad, se han observado los resultados dados en la tabla adjunta. ¿Se puede considerar que la eficacia de los 5 tratamientos es la misma, con un nivel de confianza del 95%? (Sol: \(  χ_{exp}^{2}=5.156 \). Si se puede considerar).

\(  \begin{array}{| c| c|c|c|} \hline   & CURADOS  &   NO  \hspace{.2cm} CURADOS &   TOTAL \\ \hline     TRATAMIENTO \hspace{.2cm} A  &  61  &  15 &   76  \\ \hline   TRATAMIENTO \hspace{.2cm}  B &   50  &  14  &  64 \\  \hline TRATAMIENTO \hspace{.2cm}  C  &  63 &   18 &   81 \\ \hline TRATAMIENTO \hspace{.2cm}  D &   66 &   23 &   89 \\ \hline  TRATAMIENTO \hspace{.2cm}  E  &  60 &   30 &   90 \\ \hline TOTAL  &  300  &  100  &  400 \\ \hline   \end{array}  \)

17. Se realizó una encuesta a 300 antiguos pacientes de tres hospitales sobre si estaban satisfechos con los cuidados que recibieron cuando estaban hospitalizados. Los resultados fueron los siguientes:

\(  \begin{array}{| c| c|c|c|} \hline   & Satisfechos  &  No-satisfechos  &  Total  \hspace{.2cm} fila \\ \hline
Hospital \hspace{.2cm} A  &  47 &   53   & 100 \\ \hline   Hospital \hspace{.2cm} B  &  40  &  60 &   100 \\  \hline Hospital \hspace{.2cm} C  &  27 &   73 &   100 \\ \hline Total \hspace{.2cm} columna  &  114  &  186  &  300\\ \hline   \end{array}  \)

Contrastar la hipótesis que las tres poblaciones son homogéneas con respecto a la satisfacción con los cuidados hospitalarios.(Sol: \(  χ_{exp}^{2}=8.74 \); Se rechaza \( H_0 \); por lo tanto, las tres poblaciones no parecen ser homogéneas con respecto a la característica que se investiga).

Autora: Ana María Lara Porras. Universidad de Granada

Estadística para Biología y Ciencias Ambientales. Tratamiento informático mediante SPSS. Proyecto Sur Ediciones.