ESTADÍSTICA DESCRIPTIVA: REPRESENTACIONES GRÁFICAS
Objetivos
- Resumir, ordenar y analizar conjuntos de datos
- Calcular medidas de posición, de dispersión y de forma de un conjunto de datos
- Representar gráficamente la distribución de frecuencias
- Realizar análisis exploratorios de datos.
Introducción al Análisis Descriptivo
En estadística, el análisis de datos es una mezcla de conocimientos estadísticos y sentido común. No existen unas pautas constantes para obtener unos resultados óptimos ya que cada base de datos es un problema diferente, con variables y objetivos diferentes. Sin embargo, cuando se abarca un análisis de cualquier base de datos es obligatorio estudiar la estructura de los datos, un análisis descriptivo, tanto analítico como gráfico, de los datos, etc.
El análisis exploratorio de datos es fundamental en cualquier estudio estadístico, por encima de análisis de aprendizaje de modelos estadísticos que sean capaces de predecir valores futuros, ya que si este paso no se hace con cautela no se tendrán datos de calidad y, por tanto, el modelo aprenderá de forma ineficiente.
En esta práctica tomaremos un primer contacto con las técnicas estadísticas que se utilizan para ordenar, analizar y representar un conjunto de datos, con el fin de describir apropiadamente sus características. El primer paso en el análisis de datos, una vez introducidos los mismos, es realizar un análisis descriptivo o análisis exploratorio de datos. Los principales objetivos de un análisis descriptivo o análisis exploratorio de datos son la descripción y la síntesis de los datos. Para ello, los datos se organizan en tablas, se calculan medidas que describen sus características más importantes y se realizan representaciones gráficas.
Este análisis inicial proporciona una idea de la forma que tiene la distribución de las observaciones y permite obtener estadísticos de tendencia central (media, mediana y moda), de dispersión (varianza, desviación típica, rango), de forma (asimetría, curtosis), de posición (percentiles), así como gráficos de barras, de sectores e histograma.
R y RStudio disponen de un amplio conjunto de herramientas para el análisis descriptivo de un conjunto de datos.
Estadísticos descriptivos con R-Studio
Tabla de Frecuencias
Para crear tablas de frecuencia en R y R Studio se emplea la función table o la función prop.table, dependiendo de si la tabla muestra las frecuencias absolutas o las frecuencias relativas. La sintaxis de estas órdenes es la siguiente:
> table(x) # para frecuencias absolutas
> prop.table(tab) # para las frecuencias relativas
La principal diferencia entre las dos funciones reside en el tipo de los argumentos que necesita cada una.
- table construye la tabla de frecuencias absolutas a partir de la variable que recibe como argumento
- prop.table recibe como argumento una tabla o una matriz que representa una tabla de frecuencias absolutas, y a partir de ella construye la tabla de frecuencias relativas asociada. Es decir, prop.table recibe como argumento el resultado que devuelve la función table.
Ejemplo1:
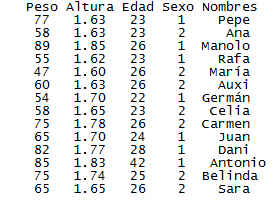
En la siguiente tabla se recogen 14 datos sobre el peso, altura, edad, sexo y nombres
En el menú principal de RStudio elegir Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H, elegir el directorio de trabajo donde estan los datos.
Y en la Consola de RStudio se muestra el comando
>setwd(“F:/Desktop/EJEMPLOS”)
A continuación seleccionamos el fichero de trabajo, al que llamamo datos. Para ello en el edtior de RStudio escribimos
Figura 1: read.table(“F:/Desktop/EJEMPLOS/ejemplo 1-RStudio.txt”, header = TRUE)
>datos <- read.table(“F:/Desktop/EJEMPLOS/ejemplo 1-RStudio.txt”, header = TRUE)
Ejecutar la sentencia, para ello Click en la tecla Run o bien presionar las teclas Ctrl+ Enter y se ejecuta, mostrándose en la Consola de RStudio
Figura 2: >datos <- read.table(“F:/Desktop/EJEMPLOS/ejemplo 1-RStudio.txt”, header = TRUE)
Nota: Se aconseja trabajar en el Editor de RStudio y ejecutar con el comando Run o bien con Ctrl+ Enter
> datos <- read.table(“F:/Desktop/EJEMPLOS/ejemplo 1-RStudio.txt”, header = TRUE)
> datos
Peso Altura Edad Sexo Nombres
1 77 1.63 23 1 Pepe
2 58 1.63 23 2 Ana
3 89 1.85 26 1 Manolo
4 55 1.62 23 1 Rafa
5 47 1.60 26 2 María
6 60 1.63 26 2 Auxi
7 54 1.70 22 1 Germán
8 58 1.65 23 2 Celia
9 75 1.78 26 2 Carmen
10 65 1.70 24 1 Juan
11 82 1.77 28 1 Dani
12 85 1.83 42 1 Antonio
13 75 1.74 25 2 Belinda
14 65 1.65 26 2 Sara
Calculamos las frecuencias absolutas y relativas de las variables peso y nombre
> tabla_peso <- table(datos$Peso)
> tabla_peso
47 54 55 58 60 65 75 77 82 85 89
1 1 1 2 1 2 2 1 1 1 1
> prop.table(tabla_peso)
47 54 55 58 60 65 75
0.07142857 0.07142857 0.07142857 0.14285714 0.07142857 0.14285714 0.14285714
77 82 85 89
0.07142857 0.07142857 0.07142857 0.07142857
> tabla_nombre <- table(datos$Nombres)
> tabla_nombre
Ana Antonio Auxi Belinda Carmen Celia Dani Germán Juan Manolo
1 1 1 1 1 1 1 1 1 1
María Pepe Rafa Sara
1 1 1 1
> prop.table(tabla_nombre)
Ana Antonio Auxi Belinda Carmen Celia Dani
0.07142857 0.07142857 0.07142857 0.07142857 0.07142857 0.07142857 0.07142857
Germán Juan Manolo María Pepe Rafa Sara
0.07142857 0.07142857 0.07142857 0.07142857 0.07142857 0.07142857 0.07142857
Representaciones gráficas
RStudio y R ofrecen una gran variedad de gráficos, el comando demo(graphics) muestra dichos gráficos. Atendiendo al tipo de datos vamos a utilizar varios tipos de gráficos.
-
- Variables cualitativas o variables cuantitativas de tipo discreto: Se pueden considerar gráficos de sectores o gráficos de barras, los cuales se obtienen en R mediante las funciones pie y barplot, respectivamente. Los argumentos más importantes de estas funciones son:
pie(x, labels = names(x), clockwise = FALSE, init.angle = if(clockwise) 90 else 0, col = NULL, main = NULL)
barplot(x, horiz = FALSE, height, col = NULL, width space, names.arg, beside, main = NULL, sub = NULL, xlab = NULL, ylab = NULL)
donde
x es un vector con las frecuencias de las observaciones. Igualmente, puede ser una tabla de frecuencia (de las obtenidas con table o prop.table)
labels es un vector de cadenas de caracteres que indican los nombres de cada una de las categorías que aparecen en el gráfico de sectores
clockwise es un argumento lógico que indica si los sectores se dibujan en sentido horario (clockwise = TRUE) o en sentido antihorario (clockwise = FALSE, que es la opción por defecto).
init.angle es un valor numérico que indica el ángulo (en grados) en el que se sitúa el primer sector. Por defecto, el primer sector empieza a dibujarse a los 90 grados (- a las 12 en punto -, cuando clockwise es igual a TRUE) o a los 0 grados (- a las 3 en punto -, cuando clockwise es igual a FALSE)
horiz es un argumento lógico que indica si las barras del gráfico de barras se dibujan de forma vertical (horiz = FALSE, que es la opción por defecto) u horizontal (horiz = TRUE)
height: vector de frecuencias para cada valor
width: especifica mediante un vector el ancho de las barras
space: fija el espacio entre las barras
names.arg: vector de nombres para colocarlos bajo las barras
beside: valor lógico, FALSE indica barras apiladas y TRUE yuxtapuestas
col es un vector en el que se indican los colores de las barras o los sectores del gráfico
main y sub son cadenas de caracteres en la que se especifican el título y el subtítulo del gráfico
xlab e ylab son cadenas de caracteres en las que se especifican los nombres de los ejes X e Y.
- Variables cuantitativas: Los gráficos que se suelen emplear con más frecuencia son el histograma, el diagrama de tallos y hojas y el diagrama de caja y bigotes. En R, se utilizan las órdenes hist, stem y boxplot para la obtención de histogramas, de diagramas de tallos y hojas y de diagramas de caja y bigotes, respectivamente. Éstas son las principales opciones de estas funciones:
hist(x, breaks = “Sturges”, freq=TRUE, right = TRUE, col = NULL, main = paste(“Histogram of” , xname))
stem(x)
boxplot(x, range = 1.5, col = NULL, main = NULL)
donde, en este caso,
x es el vector de valores de la variable a partir de los cuales se dibujará el gráfico.
breaks indica la forma en la que se calcularán los intervalos en el histograma. Las opciones disponibles para este parámetro son “Sturges” (que es la opción por defecto) “Scott” y “FD” “Freedman-Diaconis“. Para más información sobre estos métodos, así como la fórmula que emplea cada uno de ellos para determinar el número de intervalos, se puede consultar el siguiente enlace (en inglés): http://www.mas.ncl.ac.uk/~nlf8/teaching/mas1343/notes/chap4-5.pdf
freq si es TRUE determina que el intervalo se represente con las frecuencias absolutas
range es un valor numérico que determina la extensión de los bigotes de la caja. Para un valor positivo de range, los bigotes se extienden hasta el último dato que no supere 1.5 veces la longitud de la caja (el rango intercuartílico). Para un valor de 0, los bigotes se extienden hasta el dato más lejano
right es un argumento lógico que indica si los intervalos son cerrados por la izquierda y abiertos por la derecha (en cuyo caso, right = TRUE, que es la opción por defecto) o viceversa (right = FALSE).
Las opciones col y paste funcionan igual que en los gráficos de barras y sectores.
Ejemplos:
> pie(table(datos$Edad), col = c(“yellow”, “white”, “green”, “orange”,”purple”, “red”, “pink”), main = “Diagrama de sectores para la variable Edad”)
Se muestra la siguiente gráfica
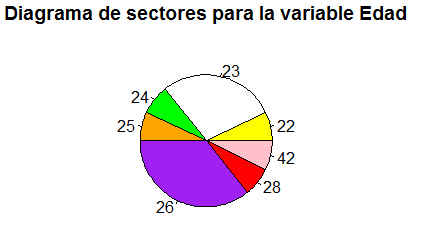Figura 2: Diagrama de sectores para la variable edad
> barplot(table(datos$Edad), col=c(“yellow”, “white”, “green”, “orange”,”purple”, “red”, “pink”), xlab=”Edad”, ylab=”Frecuencias absolutas”, main =”Diagrama de barras para la variable Edad”)
Se muestra la siguiente gráfica
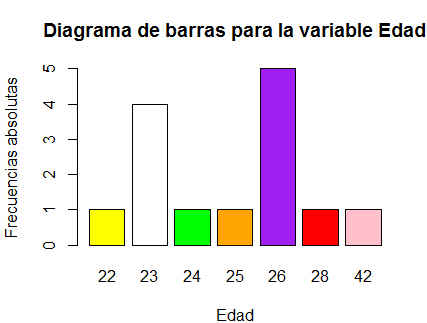Figura 3: Diagrama de barras para la variable Edad
> barplot(table(datos$Sexo,datos$Edad),col=c(2,3))
Se muestra la siguiente gráfica
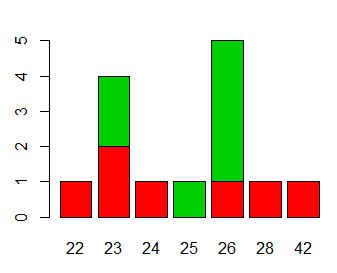Figura 4: Diagrama de barras para las variables Sexo y Edad
> hist(table(datos$Edad), col = “purple”, main = “Histograma para la variable Edad”, xlab=”Edad”, ylab=”Frecuencia”)
Se muestra la siguiente gráfica
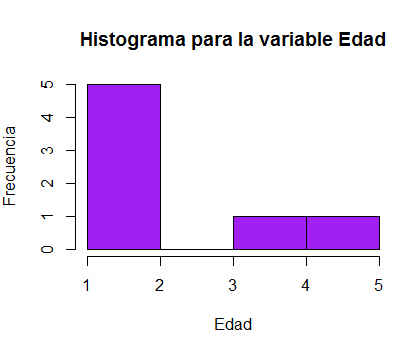Figura 5: Histograma para la variable Edad
> stem(table(datos$Peso))
The decimal point is at the |
1 | 00000000
1 |
2 | 000
> boxplot(datos$Edad, xlab=”Edad”, main = “Cajas y bigotes para la variable edad”)
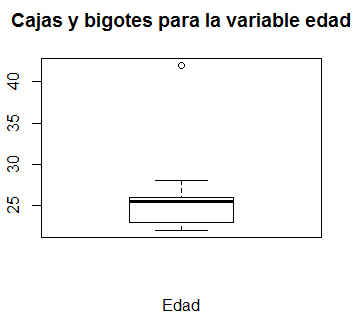Figura 6: Caja y bigotes para la variable Edad
En el Editor de RStudio hemos realizado las siguientes instrucciones
datos <- read.table(“F:/Desktop/EJEMPLOS/ejemplo 1-RStudio.txt”, header = TRUE)
datos
tabla_peso <- table(datos$Peso)
tabla_peso
prop.table(tabla_peso)
tabla_nombre <- table(datos$Nombres)
tabla_nombre
prop.table(tabla_nombre)
pie(table(datos$Edad), col = c(“yellow”, “white”, “green”, “orange”,”purple”, “red”, “pink”), main = “Diagrama de sectores para la variable Edad”)
barplot(table(datos$Edad), col=c(“yellow”, “white”, “green”, “orange”,”purple”, “red”, “pink”), xlab=”Edad”, ylab=”Frecuencias absolutas”,main =”Diagrama de barras para la variable Edad”)
barplot(table(datos$Sexo,datos$Edad),col=c(2,3))
hist(table(datos$Edad), col = “purple”, main = “Histograma para la variable Edad”, xlab=”Edad”, ylab=”Frecuencia”)
stem(table(datos$Peso))
boxplot(datos$Edad, xlab=”Edad”, main = “Cajas y bigotes para la variable edad”)
Características o Medidas de una variable estadística
En las secciones anteriores se han planteado técnicas gráficas, tablas estadísticas y representaciones gráficas, que han proporcionado una representación visual de las variables estadísticas. Dichas técnicas gráficas nos dan una idea de la composición de la población en estudio. En esta sección vamos a resumir todos los datos recogidos en una tabla estadística en unos valores, medidas numéricas, llamadas Características o Medidas que representen o sinteticen el conjunto de datos. Son medidas que proporcionan información sobre puntos importantes de la distribución, completando la información que nos ha proporcionado las tablas estadísticas y las representaciones gráficas.
Estudiaremos las Características o medidas de posición, de dispersión, y de forma
Medidas de posición
En muchas ocasiones el interés reside en localizar el centro de la distribución (para lo cual se calculan las medidas de tendencia central), existen casos en los que los puntos que se desean estudiar distan mucho de este centro (en cuyo caso se recurre al cálculo de las medidas de tendencia no central).
Algunas de las medidas más populares dentro del grupo de medidas de tendencia central son la media, la mediana y la moda. Las funciones que calculan las dos primeras medidas en R son mean y median.
mean (x, na.rm = FALSE)
median (x, na.rm = FALSE)
donde:
x: vector con los valores de la variable
na.rm: un argumento lógico que indica si hay que eliminar los valores faltantes del conjunto de datos.
Las observaciones faltantes o no disponibles de un conjunto de datos son codificadas en R como NA (que son las iniciales de Not Available). Cuando una función de R encuentra algún NA entre los valores de las observaciones que trata de analizar devuelve como resultado NA, indicando así que los cálculos no se han podido realizar. No obstante, asignando el valor TRUE al argumento na.rm se pueden eliminar los valores faltantes y obtener así un valor para la media o la mediana, basado en las observaciones restantes.
> mean(datos$Peso)
[1] 67.5
> median(datos$Peso)
[1] 65
En cuanto a la moda, R y RStudio no tienen implementada ninguna función que la calcule. Por lo que vamos a definir una función que calcule la moda de un conjunto de datos. Así, tendremos que copiar y pegar el siguiente código en el Editor de RStudio y pulsamos Run
Mode <- function(x) {
ux <- unique(x)
ux[which.max(tabulate(match(x, ux)))]
}
Una vez hecho esto, podremos calcular la moda de un conjunto de datos tal y como sigue:
Mode (x)
En el caso de que existan varias modas (es decir, cuando estemos ante una distribución plurimodal), esta función mostrará únicamente la menor de ellas (o la primera en orden alfabético, si se está analizando una variable cualitativa).
> Mode(datos$Edad)
[1] 26
Entre las medidas de posición de tendencia no central, los cuantiles figuran entre las más utilizadas. Para obtener los cuantiles de una variable en R se emplea la función quantile.
quantile(x, probs = seq(0, 1, 0.25), na.rm = FALSE)
donde:
x: vector que incluye los valores de la variable
seq: Argumento que indica los cuantiles que se van a calcular. Por defecto, se muestran los siguiente cuantiles:
- 0, que coincide con el valor mínimo
- 25, que coincide con el primer cuartil
- 50, que coincide con el segundo cuartil y con la mediana
- 75, que coincide con el tercer cuartil
- 100, que coincide con el valor máximo
na.rm: un argumento lógico que indica si hay que eliminar los valores faltantes del conjunto de datos.
> quantile(datos$Peso, probs = c(0.25, 0.75))
25% 75%
58.0 76.5
El mínimo y el máximo de un conjunto de datos, además de poder calcularse como los cuantiles 0 y 100, pueden obtenerse utilizando las funciones de R min y max.
min (x, na.rm = FALSE)
max (x, na.rm = FALSE)
> min(datos$Peso)
[1] 47
> max(datos$Peso)
[1] 89
Medidas de dispersión
Tratan de cuantificar la variabilidad o esparcimiento de los datos informando acerca de la mayor o menor representatividad de las medidas de tendencia central.
Entre las medidas de dispersión más utilizadas se encuentran la cuasi-varianza, la cuasi-desviación típica y el rango intercuartílico, que en R y RStudio se calculan a través de las funciones var, sd e IQR, respectivamente.
var(x, na.rm = FALSE)
sd(x, na.rm = FALSE)
IQR(x, na.rm = FALSE)
Los dos argumentos principales de estas funciones son x, que es el vector con los valores de la variable que se está estudiando y na.rm que, como ya se ha comentado, indica si los valores faltantes han de ser eliminados antes del análisis.
Como se ha especificado, las funciones var y sd no calculan la varianza y la desviación típica de una variable, sino su cuasi-varianza y su cuasi-desviación típica. En caso de necesitar la varianza o la desviación típica, basta con multiplicar el resultado de las funciones var y sd por (n – 1)/n, siendo n el número total de datos con el que se está trabajando.
> var(datos$Peso, na.rm = TRUE)
[1] 168.4231
> sd(datos$Peso, na.rm = TRUE)
[1] 12.97779
> IQR(datos$Peso, na.rm = TRUE)
[1] 18.5
> var_Edad <- 13/14 * var(datos$Edad)
> var_Edad
[1] 22.63776
> desvt_Edad <- sqrt(var_Edad)
> desvt_Edad
[1] 4.757915
A partir de las funciones anteriores se pueden calcular otras medidas, como el coeficiente de variación de Pearson o el rango. El coeficiente de variación se emplea para comparar la representatividad de la media entre distintas variables y se obtiene dividiendo la desviación típica de una variable entre su media. Por su parte, el rango es una medida de dispersión muy sencilla que se obtiene como la diferencia entre los valores máximo y mínimo.
> media_Edad <- mean(datos$Edad)
> media_Edad
[1] 25.92857
> CV_Edad <- desvt_Edad/media_Edad
> CV_Edad
[1] 0.1835009
Para ordenar los datos en forma creciente o decreciente se utiliza el comando sort
sort(x, decreasing = FALSE, …)
donde sus posibles argumentos son:
- x vector numérico
- na.rm valor lógico que indica si los valores de NA deben ser despojados antes de que continúe la computación
- decreasing se utiliza para indicar orden decreciente o creciente
>sort(datos$Peso)
[1] 47 54 55 58 58 60 65 65 75 75 77 82 85 89
> sort(datos$Peso, decreasing = FALSE)
[1] 47 54 55 58 58 60 65 65 75 75 77 82 85 89
> sort(datos$Peso, decreasing = TRUE)
[1] 89 85 82 77 75 75 65 65 60 58 58 55 54 47
Medidas de forma
Como su propio nombre indica, estas medidas se centran en el estudio de la forma que presenta una distribución a través del análisis de la simetría y la curtosis o el apuntamiento de la distribución en cuestión.
Para determinar la simetría de una distribución se emplea la función skewness, contenida en el paquete moments. En R y RStudio, un paquete no es más que un conjunto de funciones con un propósito común. Para poder utilizar las funciones incluidas en un determinado paquete, es necesario instalar el paquete y, posteriormente cargarlo.
Para instalar el paquete, seleccionamos en el menú principal Tools/Install Packages, y se muestra la siguiente ventana donde escribimos moments
Figura 6: Instalación del paquete “moments”
y pulsamos Install
También podemo escribir en el Editor de RStudio
install.packages(“moments”) y pulsamos Run
trying URL ‘https://cran.rstudio.com/bin/windows/contrib/3.2/moments_0.14.zip’
Content type ‘application/zip’ length 40696 bytes (39 KB)
downloaded 39 KB
package ‘moments’ successfully unpacked and MD5 sums checked
The downloaded binary packages are in
C:\Users\Usuario\AppData\Local\Temp\RtmpEXGVQk\downloaded_packages
Una vez que el paquete se ha instalado de forma correcta en nuestro ordenador no será necesario volver a instalarlo nunca más, siempre que no cambiemos la versión de R. Tras instalar el paquete, procederemos a cargarlo para ello desde el panel de paquetes simplemente se selecciona dicho paquete
Figura 7: Cargar el paquete “moments”
o bien utilizar la función library.
> library(“moments”)
A diferencia de la instalación, la carga de los paquetes es necesaria cada vez que se inicia una nueva sesión de R o de Rstudio. Una vez instalado y cargado el paquete moments, ya podemos utilizar la función skewness. Su sintaxis es:
skewness(x, na.rm = FALSE)
donde
x: es el vector que incluye los valores de la variable
na.rm: es un argumento lógico que indica si hay que eliminar los valores faltantes del conjunto de datos.
> skewness(datos$Peso)
[1] 0.177165
De forma análoga, para estudiar la curtosis de un conjunto de datos emplearemos la función kurtosis que también está contenida en el paquete moments.
kurtosis(x, na.rm = FALSE)
donde los parámetros x y na.rm se definen forma similar al caso anterior.
> kurtosis(datos$Peso)
[1] 1.810379
Algunas funciones resumen
Existen funciones en R que calculan, a la vez, algunas de las medidas que se han descrito hasta ahora, summary es un buen ejemplo de este tipo de funciones, ya que cuando se aplica a una variable cuantitativa devuelve el mínimo, el máximo, la media, la mediana y los cuartiles primero y tercero de la variable. La sintaxis de esta función es la siguiente:
summary(object)
object: es el objeto (la variable en nuestro caso) del cual queremos obtener el resumen.
> summary(datos$Peso)
Min. 1st Qu. Median Mean 3rd Qu. Max.
47.0 58.0 65.0 67.5 76.5 89.0
En el Editor de RStudio hemos realizado las siguientes instrucciones
datos <- read.table(“F:/Desktop/EJEMPLOS/ejemplo 1-RStudio.txt”, header = TRUE)
mean(datos$Peso)
median(datos$Peso)
Mode(datos$Edad)
quantile(datos$Peso, probs = c(0.25, 0.75))
min(datos$Peso)
max(datos$Peso)
var(datos$Peso, na.rm = TRUE)
sd(datos$Peso, na.rm = TRUE)
IQR(datos$Peso, na.rm = TRUE)
var_Edad <- 13/14 * var(datos$Edad)
var_Edad
desvt_Edad <- sqrt(var_Edad)
desvt_Edad
media_Edad <- mean(datos$Edad)
CV_Edad <- desvt_Edad/media_Edad
CV_Edad
sort(datos$Peso)
sort(datos$Peso, decreasing = TRUE)
install.packages(“moments”) # Es necesario si aún no se ha instalado
library(“moments”)
skewness(datos$Peso)
kurtosis(datos$Peso)
summary(datos$Peso)
Ejercicios
Ejercicios Guiados
Ejercicio guiado
Considérese el siguiente conjunto de datos que contiene información acerca del sexo, edad, estatura, puntuación y calificación de 20 estudiantes:
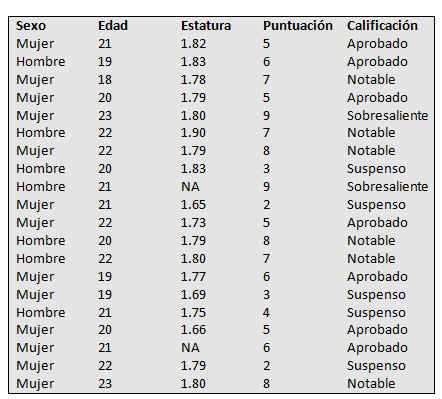Tabla2. Datos del Ejercicio Guiado 1
a) Realiza una tabla de frecuencias absolutas y otra de frecuencias relativas para la variable Calificación. Almacena las tablas anteriores en dos variables y llámalas absolutas y relativas.
b) Representa la variable Calificación mediante un diagrama de barras y un diagrama de sectores. Incluye un título adecuado para cada gráfico y colorea las barras y los sectores de colores diferentes.
c) Para la variable Edad, realiza un histograma y un diagrama de caja y bigotes considerando la opción range = 1.5. Incluye un título apropiado para cada gráfico y colorea las barras del histograma de color amarillo. ¿Existe algún valor atípico en esta variable? Reduce el valor del argumento range hasta 0.5. ¿Varían las conclusiones?
d) Realiza un resumen de la variable Puntuación mediante la orden summary. Comprueba que las medidas que proporciona summary coinciden con las medidas calculadas de forma individual usando su función específica.
e) Calcula la estatura media de los estudiantes y proporciona, al menos, dos medidas que indiquen la dispersión de esta variable.
f) ¿Qué variable es más homogénea: la Edad o la Estatura?
Ejercicio Guiado (Resuelto)
Considérese el siguiente conjunto de datos que contiene información acerca del sexo, edad, estatura, puntuación y calificación de 20 estudiantes:
a) Realiza una tabla de frecuencias absolutas y otra de frecuencias relativas para la variable Calificación. Almacena las tablas anteriores en dos variables y llámalas absolutas y relativas.
En primer lugar, nos situamos en el directorio de trabajo. Para ello, en el menú principal de RStudio, seleccionamos Session/Set Working Directory/Choose Directory o bien con las teclas Ctrl+Shift+H,
Y en la Consola de RStudio se muestra el comando
>setwd(“F:/Desktop/EJEMPLOS”)
Utilizamos la función read.table para leer un fichero .txt en R y llamamos al fichero datos1
> datos1 <- read.table(“C:/Users/Usuario/Desktop/EJEMPLOS/Ej_Guiado1.txt”, header = TRUE)
> datos1
Sexo Edad Estatura Puntuación Calificación
1 Mujer 21 1.82 5 Aprobado
2 Hombre 19 1.83 6 Aprobado
3 Mujer 18 1.78 7 Notable
4 Mujer 20 1.79 5 Aprobado
5 Mujer 23 1.80 9 Sobresaliente
6 Hombre 22 1.90 7 Notable
7 Mujer 22 1.79 8 Notable
8 Hombre 20 1.83 3 Suspenso
9 Hombre 21 NP 9 Sobresaliente
10 Mujer 21 1.65 2 Suspenso
11 Mujer 22 1.73 5 Aprobado
12 Hombre 20 1.79 8 Notable
13 Hombre 22 1.80 7 Notable
14 Mujer 19 1.77 6 Aprobado
15 Mujer 19 1.69 3 Suspenso
16 Hombre 21 1.75 4 Suspenso
17 Mujer 20 1.66 5 Aprobado
18 Mujer 21 NP 6 Aprobado
19 Mujer 22 1.79 2 Suspenso
20 Mujer 23 1.80 8 Notable
> absolutas <- table(datos1$Calificación)
> absolutas
Aprobado Notable Sobresaliente Suspenso
7 6 2 5
> relativas <- prop.table(absolutas)
> relativas
Aprobado Notable Sobresaliente Suspenso
0.35 0.30 0.10 0.25
b) Representa la variable Calificación mediante un diagrama de barras y un diagrama de sectores. Incluye un título adecuado para cada gráfico y colorea las barras y los sectores de colores diferentes.
> barplot(absolutas, col = c(“red”, “blue”, “yellow”, “green”), main = “Diagrama de barras para la variable Calificación”)
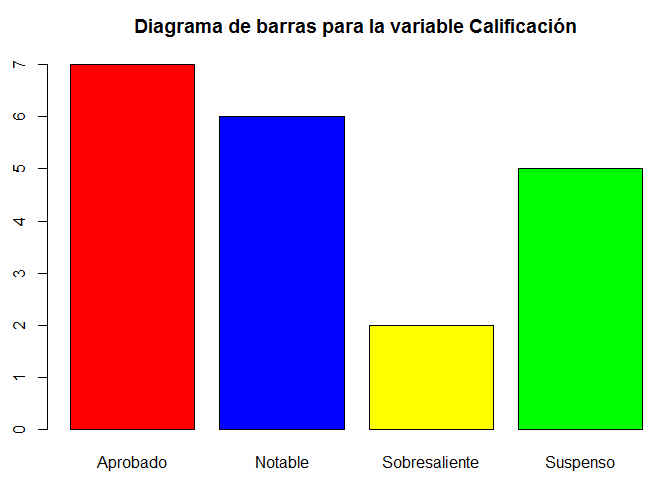Figura 8: Diagrama de barras de la variable Calificación
> pie(absolutas, col = c(“red”, “blue”, “yellow”, “green”), main = “Diagrama de barras para la variable Calificación”)
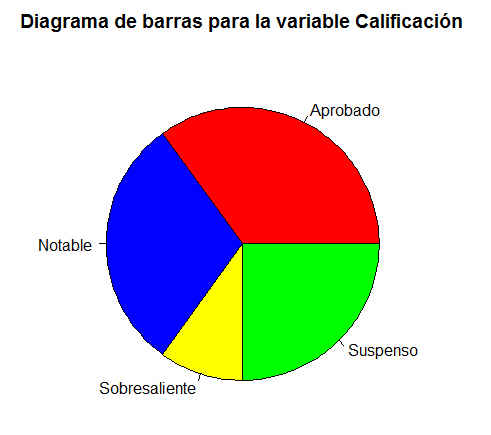Figura 9: Diagrama de sectores de la variable Calificación
c) Para la variable Edad, realiza un histograma y un diagrama de caja y bigotes considerando la opción range = 1.5. Incluye un título apropiado para cada gráfico y colorea las barras del histograma de color amarillo. ¿Existe algún valor atípico en esta variable? Reduce el valor del argumento range hasta 0.5. ¿Varían las conclusiones?
> hist(datos1$Edad, col = “yellow”, main = “Histograma para la variable Edad”, xlab = “Edades”, ylab = “Frecuencia”)
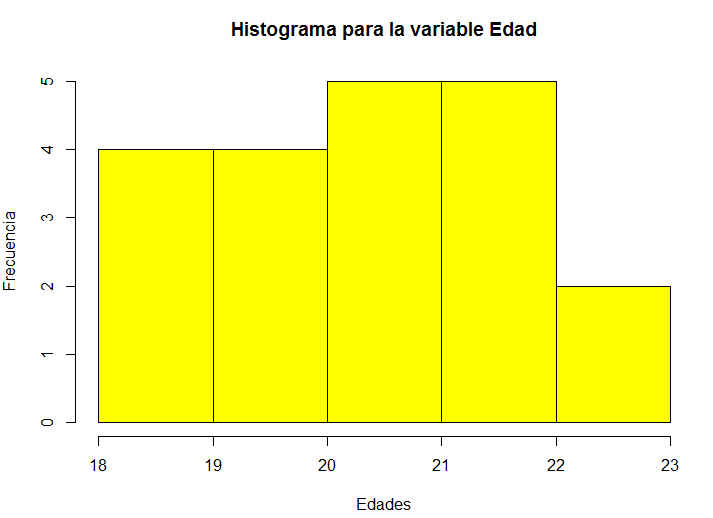Figura 10: Histograma de la variable Edad
> boxplot(datos1$Edad, main = “Cajas y bigotes para la variable Edad (range = 1.5)”)
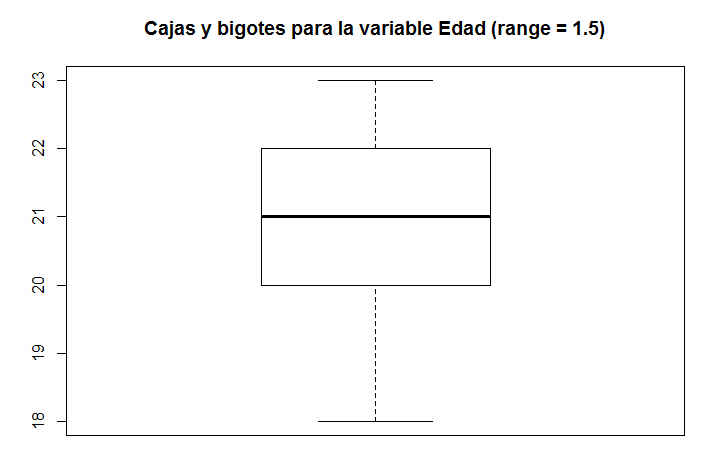Figura 11: Caja y Bigotes de la variable Edad (range = 1.5)
En este caso no se aprecia ningún valor atípico en el diagrama de caja y bigotes, ya que no aparece ningún valor más allá de los bigotes.
> boxplot(datos1$Edad, main = “Cajas y bigotes para la variable Edad (range = 0.5)”)
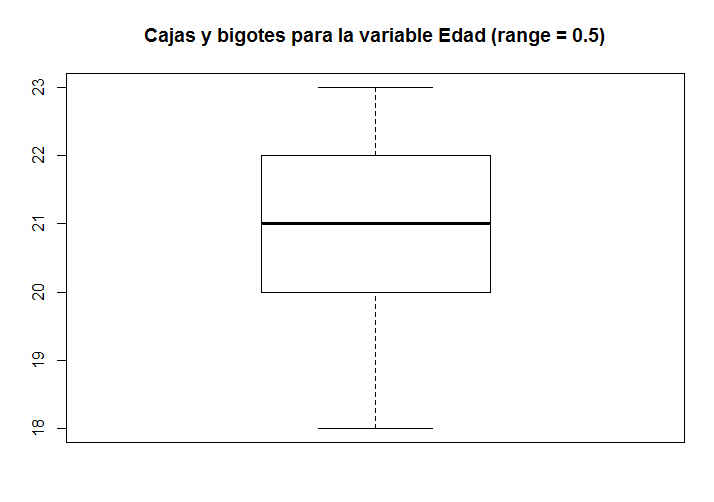Figura 12: Caja y Bigotes de la variable Edad (range = 0.5)
Cuando se reduce el valor de range a 0.5 tampoco se observa ningún valor atípico.
d) Realiza un resumen de la variable Puntuación mediante la orden summary. Comprueba que las medidas que proporciona summary coinciden con las medidas calculadas de forma individual usando su función específica.
Si aplicamos la función summary a la variable Puntuación, obtenemos el siguiente resultado
> summary(datos1$Puntuación)
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.00 4.75 6.00 5.75 7.25 9.00
Calculemos cada medida por separado
> min(datos1$Puntuación)
[1] 2
> max(datos1$Puntuación)
[1] 9
> quantile(datos1$Puntuación, probs = c(0.25, 0.75))
25% 75%
4.75 7.25
> mean(datos1$Puntuación )
[1] 5.75
> median(datos1$Puntuación)
[1] 6
e) Calcula la estatura media de los estudiantes y proporciona, al menos, dos medidas que indiquen la dispersión de esta variable.
Para calcular la estatura media de los estudiantes, tenemos que tener en cuenta que la variable Estatura incluye dos valores faltantes entre sus observaciones. Este hecho tiene que ser indicado estableciendo como TRUE el valor del parámetro na.rm
> mean(datos1$Estatura, na.rm = TRUE)
[1] 1.776111
La estatura media de los estudiantes es de 1.776 cm..
Como medidas de dispersión, se van a calcular la cuasi-varianza y el recorrido intercuartílico.
> var(datos1$Estatura, na.rm = TRUE)
[1] 0.003836928
> IQR(datos1$Estatura, na.rm = TRUE)
[1] 0.045
f) ¿Qué variable es más homogénea: la edad o la estatura?
Para determinar la homogeneidad de una variable (o, lo que es lo mismo, la representatividad de su media), calculamos el Coeficiente de Variación de Pearson para cada una de ellas, el cual se define como el cociente entre la desviación típica y la media de la variable.
Vamos a comenzar con la variable Edad. En primer lugar, calculemos la edad media de los estudiantes.
> media_Edad <- mean(datos1$Edad)
> media_Edad
[1] 20.8
A continuaciñon obtenemos la desviación típica. Para ello, calcularemos en primer lugar la varianza de la variable Edad mediante la función var, que recordemos calcula la cuasi-varianza de una variable.
> var_Edad <- 19/20 * var(datos1$Edad)
> var_Edad
[1] 1.86
Una vez obtenida la varianza, la desviación típica se obtiene como su raíz cuadrada positiva.
> dt_Edad <- sqrt(var_Edad)
> dt_Edad
[1] 1.363818
Por último, calculamos el Coeficiente de Variación de la Edad y mostramos su valor.
> CV_Edad <- dt_Edad/media_Edad
> CV_Edad
[1] 0.06556818
Repetimos el mismo proceso con la variable Estatura.
> media_Altura <- mean(datos1$Estatura, na.rm = TRUE)
> var_Altura <- 19/20 * var(datos1$Estatura, na.rm = TRUE)
> dt_Altura <- sqrt(var_Altura)
> CV_Altura <- dt_Altura/media_Altura
> CV_Altura
[1] 0.03399253
La variable más homogénea es la variable Estatura, ya que presenta un coeficiente de variación más próximo a 0.
En el Editor de RStudio hemos realizado las siguientes instrucciones
datos1 <- read.table(“C:/Users/Usuario/Desktop/EJEMPLOS/Ej_Guiado1.txt”, header = TRUE)
datos1
absolutas <- table(datos1$Calificación)
absolutas
relativas <- prop.table(absolutas)
relativas
barplot(absolutas, col = c(“red”, “blue”, “yellow”, “green”), main = “Diagrama de barras para la variable Calificación”)
pie(absolutas, col = c(“red”, “blue”, “yellow”, “green”), main = “Diagrama de barras para la variable Calificación”)
hist(datos1$Edad, col = “yellow”, main = “Histograma para la variable Edad”, xlab = “Edades”, ylab = “Frecuencia”)
boxplot(datos1$Edad, main = “Cajas y bigotes para la variable Edad (range = 1.5)”)
boxplot(datos1$Edad, main = “Cajas y bigotes para la variable Edad (range = 0.5)”)
summary(datos1$Puntuación)
min(datos1$Puntuación)
max(datos1$Puntuación)
quantile(datos1$Puntuación, probs = c(0.25, 0.75))
mean(datos1$Puntuación )
median(datos1$Puntuación)
mean(datos1$Estatura, na.rm = TRUE)
var(datos1$Estatura, na.rm = TRUE)
IQR(datos1$Estatura, na.rm = TRUE)
media_Edad <- mean(datos1$Edad)
media_Edad
var_Edad <- 19/20 * var(datos1$Edad)
var_Edad
dt_Edad <- sqrt(var_Edad)
dt_Edad
CV_Edad <- dt_Edad/media_Edad
CV_Edad
media_Altura <- mean(datos1$Estatura, na.rm = TRUE)
var_Altura <- 19/20 * var(datos1$Estatura, na.rm = TRUE)
dt_Altura <- sqrt(var_Altura)
CV_Altura <- dt_Altura/media_Altura
CV_Altura
Ejercicios Propuestos
Ejercicio Propuesto
Se está realizando un estudio sobre los niveles de glucosa en una población con el objetivo de estudiar si dichos niveles varían en función del sexo, edad, estatura y grupo sanguíneo de la persona. Para ello se toman dos muestras de 20 individuos cada una
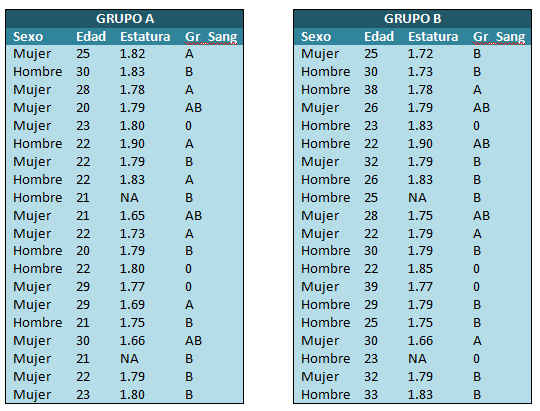Tabla3. Datos del Ejercicio Propuesto 1
Se pide:
a) Crear dos conjuntos de datos, de nombre GrA y GrB que contengan la información recogida en las tablas anteriores.
b) Representar la variable Gr_Sang mediante un diagrama de sectores en cada uno de los grupos. Incluir un título descriptivo en cada gráfico y colorear los sectores de azul, amarillo, rosa y verde.
c) Representar la variable Estatura mediante un histograma en cada uno de los grupos.
d) ¿Existe algún dato atípico en la variable Edad en el grupo A? ¿Y en el grupo B?
e) ¿Cuál es el valor máximo del 40% de las estaturas más pequeñas de los individuos en el grupo A? ¿Y el valor mínimo del 30% de las estaturas mayores de los individuos en el grupo B?
f) ¿Dónde son las variables edad y estatura más homogénea: en el grupo A o en el B?
g) ¿En qué grupo presentan los individuos una altura media mayor? ¿En qué grupo presentan los individuos una altura mediana menor?
h) Estudia la asimetría y la curtosis de la variable Estatura en en el grupo A.
Ejercicio Propuesto (Resuelto)
a) Crear dos conjuntos de datos, de nombre GrA y GrB que contengan la información recogida en las tablas anteriores.
>Sexo_A <- factor(c(“Mujer”, “Hombre”, “Mujer”, “Mujer”, “Mujer”, “Hombre”, “Mujer”, “Hombre”, “Hombre”, “Mujer”, “Mujer” ,”Hombre”, “Hombre”, “Mujer”, “Mujer”, “Hombre”, “Mujer”, “Mujer”, “Mujer”, “Mujer” ), levels = c(“Mujer”, “Hombre”))
>Edad_A <- c(25, 30, 28, 20, 23, 22, 22, 22, 21, 21, 22, 20, 22, 29, 29, 21, 30, 21, 22, 23)
>Estatura_A <- c(1.82, 1.83, 1.78, 1.79, 1.80, 1.90, 1.79, 1.83, NA, 1.65, 1.73, 1.79, 1.80, 1.77, 1.69, 1.75, 1.66, NA, 1.79, 1.80)
>Gr_Sang_A <- c(“A”, “B”, “A”, “AB”, “0”, “A”, “B”, “A”, “B”, “AB”, “A”, “B”, “0”, “0”, “A”, “B”, “AB”, “B”, “B”, “B”)
> GrA<- data.frame (Sexo_A,Edad_A, Estatura_A, Gr_Sang_A)
> GrA
Sexo_A Edad_A Estatura_A Gr_Sang_A
1 Mujer 25 1.82 A
2 Hombre 30 1.83 B
3 Mujer 28 1.78 A
4 Mujer 20 1.79 AB
5 Mujer 23 1.80 0
6 Hombre 22 1.90 A
7 Mujer 22 1.79 B
8 Hombre 22 1.83 A
9 Hombre 21 NA B
10 Mujer 21 1.65 AB
11 Mujer 22 1.73 A
12 Hombre 20 1.79 B
13 Hombre 22 1.80 0
14 Mujer 29 1.77 0
15 Mujer 29 1.69 A
16 Hombre 21 1.75 B
17 Mujer 30 1.66 AB
18 Mujer 21 NA B
19 Mujer 22 1.79 B
20 Mujer 23 1.80 B
b) Representar la variable Gr_Sang mediante un diagrama de sectores en cada uno de los grupos. Incluir un título descriptivo en cada gráfico y colorear los sectores de azul, amarillo, rosa y verde.
> pie(table(GrA$Gr_Sang_A), col = c( “blue”, “yellow”, “pink”, “green”), main = “Diagrama de sectores para Grupo Sanguineo (Gr A)”)
Figura 14: Diagrama de Sectores del Grupo Sanguíneo (Grupo A)
Figura 15: Diagrama de Sectores del Grupo Sanguíneo (Grupo B)
c) Representar la variable Estatura mediante un histograma en cada uno de los grupos.
Histograma de Altura en el Grupo A
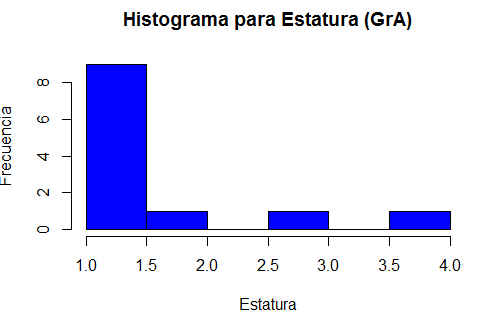Figura 16: Histograma de la estatura (Grupo A)
Histograma de la Estatura para el Grupo B
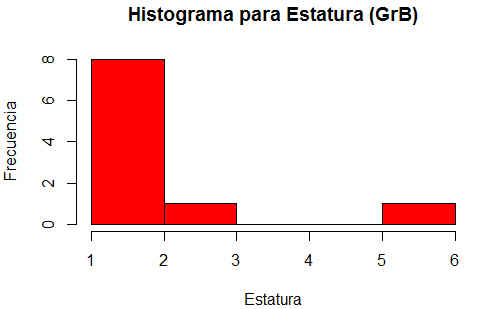Figura 17: Histograma de la estatura (Grupo B)
d) ¿Existe algún dato atípico en la variable Edad en el grupo A? ¿Y en el grupo B?
Para responder a esta pregunta, vamos a calcular los gráficos de caja y bigotes para la variable Edad en ambos grupos.
Boxplot de Edad para el Grupo A
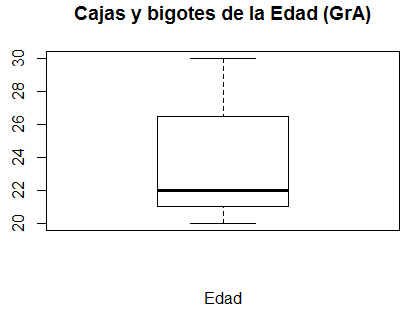Figura 18: Caja y Bigotes de la edad (Grupo A)
Boxplot de Edad para el Grupo B
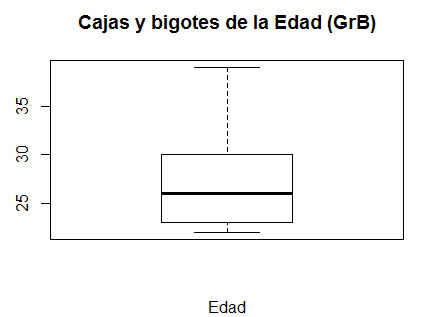Figura 19: Caja y Bigotes de la edad (Grupo B)
No hay valores atípicos (datos más allá de los extremos de los bigotes) para la variable Edad en ninguno de los grupos.
e) ¿Cuál es el valor máximo del 40% de las estaturas más pequeñas de los individuos en el grupo A? ¿Y el valor mínimo del 30% de las estaturas mayores de los individuos en el grupo B?
Los valores que nos están pidiendo son el percentil 40 de la variable Estatura en la región A y el percentil 70 de la variable Altura en la región B, respectivamente.
Percentil 40 de Estatura en el Grupo A = 1.79
Percentil 70 de Estatura en el Grupo B = 1.79
f) ¿Dónde son las variablea edad y estatura más homogénea: en el grupo A o en el B?
Para contestar a esta pregunta, vamos a calcular el Coeficiente de Variación de Pearson para la variable Estatura en cada uno de los grupos. Recordemos que la fórmula para el cómputo del coeficiente de variación es
\( CV= \displaystyle \frac{\sigma} {| \overline {x} | } \)
Por lo tanto,
CV de la Estatura del Grupo A = 0.5813903
CV de la Estatura del Grupo B =0.02937938
Atendiendo a los resultados que hemos obtenido, podemos afirmar que la variable Estatura es más homogénea en el Grupo B dado que es en esta región donde el coeficiente de variación para la variable Estatura está más próximo a 0.
g) ¿En qué grupo presentan los individuos una altura media mayor? ¿En qué grupo presentan los individuos una altura mediana menor?
Como se puede apreciar, la estatura media mayor es en el Grupo A.
h) Estudia la asimetría y la curtosis de la variable Estatura en en el grupo A.
Asimetría de la Estatura en el Grupo A = 3.863992
Kurtosis de la Estatura en el Grupo A = 15.97886
Como el coeficiente de asimetría es mayor que 0, concluiremos que la distribución de la variable Estatura en el Grupo A es asimétrica a la derecha. Igualmente, dado que el coeficiente de curtosis es también positivo, la distribución de esta variable es más apuntada que la distribución normal es decir, leptocúrtica.
Ejercicio Propuesto 1 (Resuelto *.txt)
Autora: Ana María Lara Porras. Universidad de Granada. (2017)