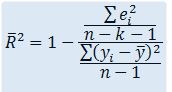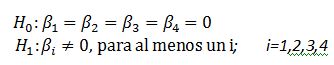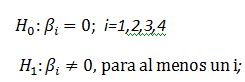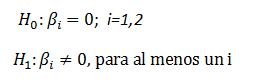REGRESIÓN Y CORRELACIÓN
Objetivos
- Representar el diagrama de dispersión
- Ajustar una recta de regresión a las observaciones
- Analizar la bondad del ajuste lineal
- Ajustar una curva parabólica a las observaciones
- Analizar la bondad del ajuste parabólico
- Comparar el ajuste lineal y el parabólico
- Otros tipos de ajustes
- APÉNDICE: Regresión múltiple
Introducción
En esta práctica estudiamos dos tipos de problemas. El primero es el de encontrar una función que se ajuste lo mejor posible a un conjunto de puntos observados, gráficamente equivale a encontrar una curva que aunque no pase por todos los puntos esté lo más próxima posible de dichos puntos. El segundo es medir el grado de ajuste entre la función teórica (función ajustada) y la nube de puntos. Distinguimos así, entre Teoría de Regresión y Teoría de Correlación.
-
Teoría de Regresión: Consiste en la búsqueda de una “función” que exprese lo mejor posible el tipo de relación entre dos o más variables. Esta práctica sólo estudia la situación de dos variables.Una de las aplicaciones más interesante que tiene la Regresión es la de Predecir, es decir, conocido el valor de una de las variables, estimar el valor que presentará la otra variable relacionada con ella.
-
Teoría de Correlación: Estudia el grado de dependencia entre las variables es decir, su objetivo es medir el grado de ajuste existente entre la función teórica (función ajustada) y la nube de puntos.Cuando la relación funcional que liga las variables X e Y es una recta entonces la regresión y correlación reciben el nombre de Regresión Lineal y Correlación Lineal. Una medida de la Correlación Lineal la da el Coeficiente de Correlación Lineal de Pearson.
Regresión y Correlación Lineal
El objetivo del Análisis de regresión consiste en la búsqueda de una función matemática sencilla que exprese lo mejor posible el tipo de relación entre dos o más variables, que describa el comportamiento de una variable dados los valores de otra u otras variables.
El Análisis de regresión simple, estudia y explica el comportamiento de una variable que notamos Y, que recibe el nombre de variable dependiente, variable de interés o variable explicada, a partir de otra variable, que notamos X, y que llamamos variable explicativa, variable de predicción o variable independiente.
La regresión lineal simple supone que los valores de la variable dependiente, a los que notaremos yi, pueden escribirse en función de los valores de una única variable independiente, los cuales notaremos por xi, según el siguiente modelo lineal:
\( y_i = \widehat{\beta}_0 + \widehat{\beta}_1 x_i + \epsilon_i \hspace{1cm} i=1,2, …, n \)
Fómula 1: Regresión lineal simple
donde \( \beta_0 \) y \( \beta_1 \), son los parámetros desconocidos que vamos a estimar y \( \epsilon_i \) e \( y_i \) son variables aleatorias. \( \epsilon_i \) recibe el nombre de error aleatorio o perturbación.
Al iniciar un estudio de regresión lineal simple, el primer paso que debe realizar el investigador es representar las observaciones de ambas variables en un gráfico llamado diagrama de dispersión o nube de puntos. A partir de esta representación el investigador determina si realmente existe una relación lineal entre ambas variables.
se muestra la siguiente ventana
Se selecciona la opción que se desee representar, que en nuestro caso es Dispersión simple y se pulsa el botón Definir. En la ventana correspondiente se sitúan las variables X e Y en su lugar correspondiente.
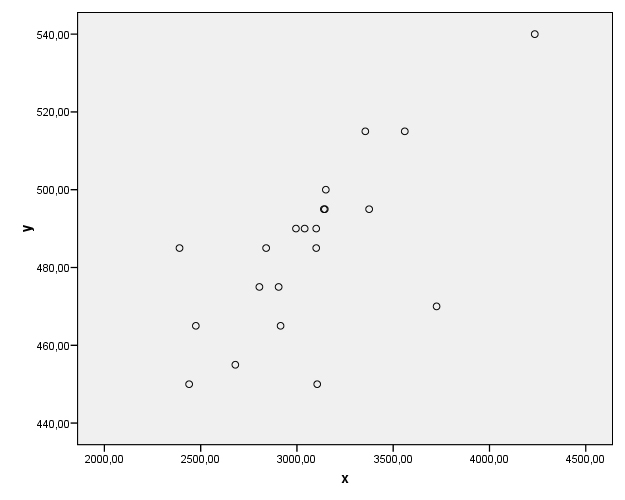
Se pulsa Aceptar y se muestra el gráfico de dispersión
El gráfico muestra una posible adecuación del modelo lineal y la tendencia creciente del mismo.
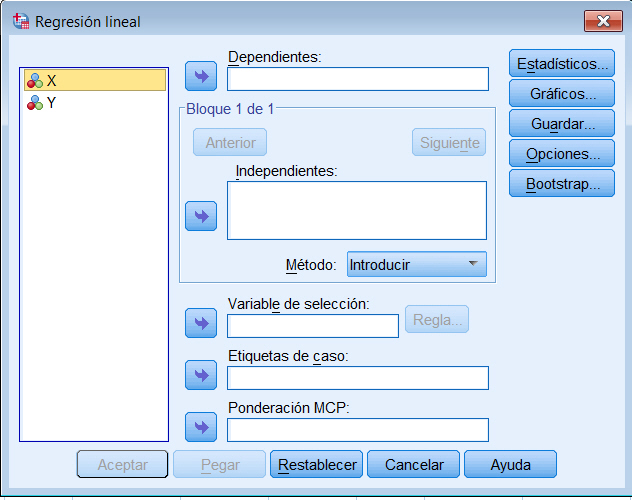
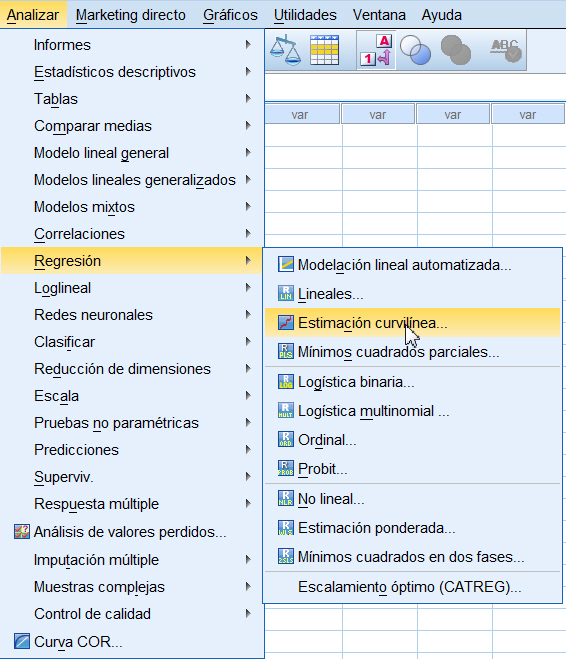
Para obtener la recta de regresión mínima cuadrática de Y sobre X, \( y = b_0 + b_1 x \), se debe elegir el procedimiento Regresión lineal. Para ello se selecciona Analizar/Regresión/Lineales…
Se muestra la siguiente ventana
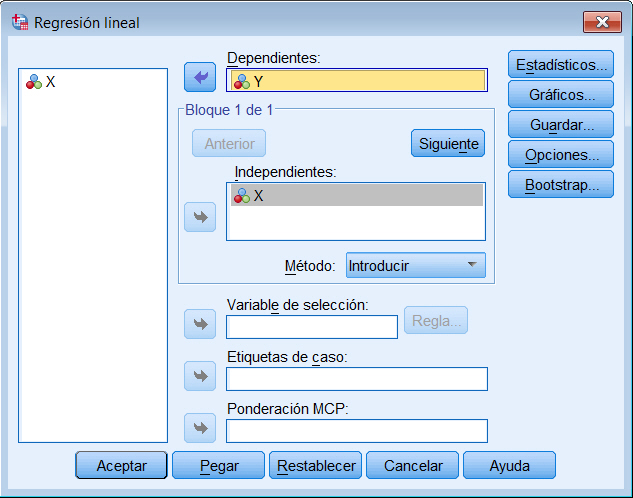
Se desplazan las variables X e Y a su campo correspondiente
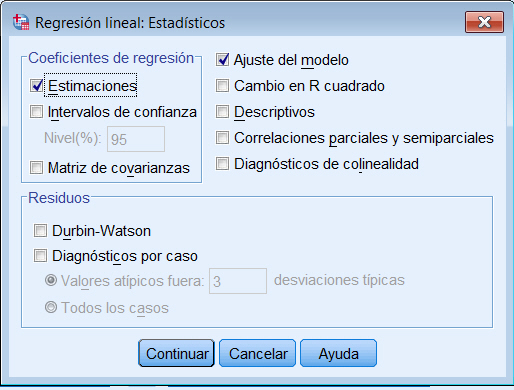
Se pulsa el botón Estadísticos…
donde se selecciona en Coeficientes de regresión: Estimaciones e Intervalos de confianza y se marca Ajuste del modelo. Se pulsa Continuar.
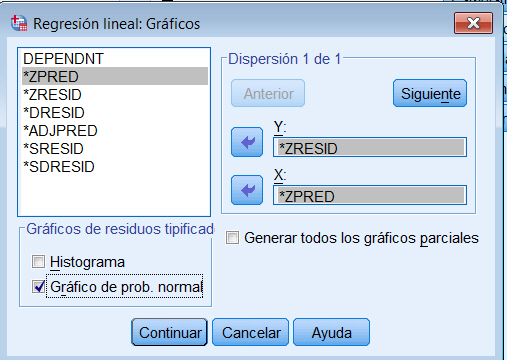
Se pulsa el botón Gráficos…
donde se elige *ZRESID para Y y *ZPRED para X. Por último se marca la opción Gráfico de prob. normal. Se pulsa Continuar
Las representaciones gráficas son una forma de juzgar visualmente la bondad de ajuste y de detectar comportamientos extraños de observaciones individuales, valores atípicos. Una visión global de la gráfica nos puede orientar sobre el cumplimiento de los supuestos del modelo: Normalidad, Linealidad y Homocedasticidad (Igualdad de las Varianzas) e Independencia de los Residuos. Además de representar un Histograma y un Gráfico Probabilístico Normal, también se pueden confeccionar diversos gráficos que aportan información sobre el cumplimiento de las hipótesis del modelo. Así se pueden realizar Diagramas de Dispersión para cualquier combinación de las siguientes variables: la variable dependiente, los valores pronosticados (ajustados o predichos), residuos tipificados (estandarizados), los residuos eliminados (sin considerar el caso), ajustados en función de los valores pronosticados, residuos estudentizados, o residuos estudentizados eliminados (sin considerar el caso).
Por ejemplo:
Gráfico de Residuos tipificados/Valores pronosticados tipificados o simplemente Residuos/Valor predicho: Este gráfico se utiliza para comprobar las hipótesis de Linealidad y de Homocedasticidad y estudiar si el modelo es adecuado o no. Si en el gráfico observamos alguna tendencia, ésta puede ser indicio de autocorrelación, de heterocedasticidad o falta de linealidad. En general no se debe observar ninguna tendencia ni comportamiento anómalo.
Gráfico de Valores Observados/Valores predichos: Este gráfico incluye una línea de pendiente 1. Si los puntos están sobre la línea indican que todas las predicciones son perfectas. Como el gráfico anterior, también se utiliza para comprobar la hipótesis de igualdad de varianzas, así se detecta los casos en que la varianza no es constante y se determina si es preciso efectuar una transformación de los datos que garantice la homocedasticidad.
Gráfico de Residuos/Variable X: Este gráfico que representa los residuos frente a una variable independiente, permite detectar la adecuación del modelo con respecto a la variable independiente seleccionada y también detecta si la varianza de los residuos es constante en relación a la variable independiente seleccionada. Si en este gráfico observamos alguna tendencia nos puede indicar el incumplimiento de la hipótesis de homocedasticidad o falta de linealidad, así como autocorrelación.
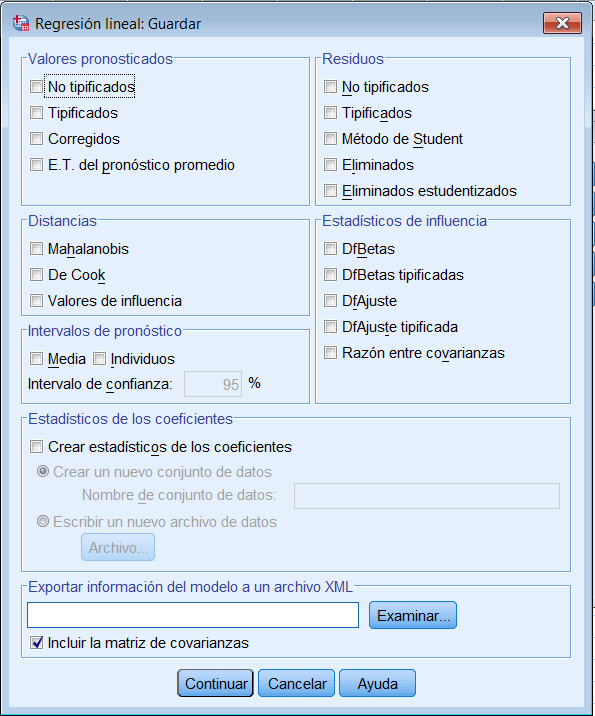
Se pulsa el botón Guardar…
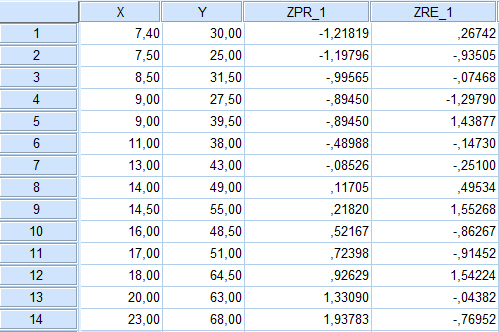
y en Valores pronosticados y Residuos se elige Tipificados. Se pulsa Continuar. En la ventana del Editor de datos se han creado dos variables con los nombres ZPR_1 (para los valores pronosticados tipificados) y ZRE_1 (para los residuos tipificados).
Se pulsa Continuar y Aceptar. Y se obtienen, entre otros, los siguientes resultados
Coeficiente de correlación (R). Este coeficiente es una medida de la asociación lineal que existe entre las variables x e y.
Se define por
\( r = \displaystyle \frac {Cov(x,y)}{\sigma_x \sigma_y} , \hspace{1cm} con \hspace{.2cm} -1 \leq r \leq 1 \)
- r = -1⇒ asociación lineal negativa perfecta entre x e y
- r = 1 ⇒ asociación lineal positiva perfecta entre x e y
- r = 0 ⇒ no existe ninguna asociación lineal entre x e y
Coeficiente de determinación (R cuadrado)
Es una medida relativa del grado de asociación lineal entre x e y. Se define de la siguiente forma
\( \begin{array} {rl} R^2 & = \displaystyle \frac {Sumas \hspace{.2cm} de \hspace{.2cm} cuadrados \hspace{.2cm} Regresión} {Sumas \hspace{.2cm} de \hspace{.2cm} cuadrados \hspace{.2cm} total} = \displaystyle \frac {SCReg}{SCT} \\ \\ & = 1 – \displaystyle \frac {Sumas \hspace{.2cm} de \hspace{.2cm} cuadrados \hspace{.2cm} Residual}{Sumas \hspace{.2cm} de \hspace{.2cm} cuadrados \hspace{.2cm} total} = 1- \displaystyle \frac {SCR}{SCT} \\ \end{array} \)
Este coeficiente representa la proporción de variación de y explicada por el modelo de regresión. Por construcción, es evidente que \( 0 ≤ R^2 ≤1 \)
- Si \( R^2 =1 \), entonces SCReg = SCT, por lo que toda la variación de y es explicada por el modelo de regresión
- Si \( R^2 =0 \), entonces SCR=SCT, por lo que toda la variación de y queda sin explicar.
En general, cuanto más próximo esté a 1, mayor es la variación de y explicada por el modelo de regresión.
Esta tabla muestra los resultados del ajuste del modelo de regresión. El valor de R cuadrado, que corresponde al coeficiente de determinación, mide la bondad del ajuste de la recta de regresión a la nube de puntos, el rango de valores es de 0 a 1. Valores pequeños de R cuadrado indican que el modelo no se ajusta bien a los datos. R cuadrado = 0.481 indica que el 48.1% de la variabilidad de Y es explicada por la relación lineal con X. El valor R (0.694) representa el valor absoluto del Coeficiente de Correlación, es decir es un valor entre 0 y 1. Valores próximos a 1 indican una fuerte relación entre las variables. La última columna nos muestra el Error típico de la estimación (raíz cuadrada de la varianza residual) con un valor igual a 16.52243
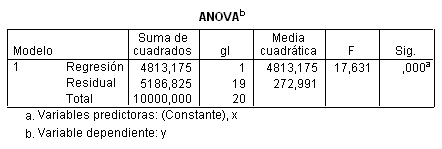
En la Tabla ANOVA, se muestra la descomposición de la Variabilidad Total (SCT = 10000) en la Variabilidad debida a la Regresión (\( SCR_{eg} = 4813.175 \)) y la Variabilidad Residual (SCR = 5186.825) es decir en Variabilidad explicada por el modelo de regresión y la Variabilidad no explicada. \( SCT = SCR_{eg} + SCR \). La Tabla de Ánalisis de la Varianza (Tabla ANOVA) se construye a partir de esta descomposición y proporciona el valor del estadístico F que permite contrastar la hipótesis nula de que la pendiente de la recta de regresión es igual a cero contra la alternativa de que la pendiente es distinta de cero, es decir:
\( \begin{array} \\ H_0 \equiv \beta_1 = 0 \\ H_1 \equiv \beta_1 \neq 0 \end{array}\)
donde H0 se conoce, en general, como hipótesis de no linealidad entre X e Y
La Tabla ANOVA muestra el valor del estadístico de contraste, F = 17.631, que se define como el cociente entre el Cuadrado medio debido a la regresión (CMR_{eg} = 4813.175) y el Cuadrado medio residual (CMR = 272.991), por tanto cuanto mayor sea su valor, mejor será la predicción mediante el modelo lineal. El p-valor asociado a F, en la columna Sig, es menor que 0.001, menor que el nivel de significación α = 0.05, lo que conduce a rechazar la hipótesis nula, es decir existe una relación lineal significativa entre Y y X. Esto indica que es válido el modelo de regresión considerado, en este caso el modelo lineal simple. Sin embargo, esto no significa que este modelo sea el único válido, puesto que pueden existir otros modelos también válidos para predecir la variable dependiente.
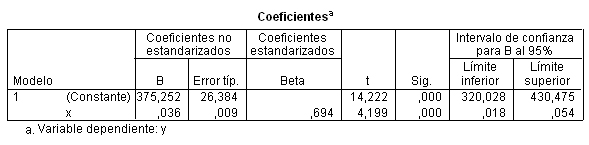
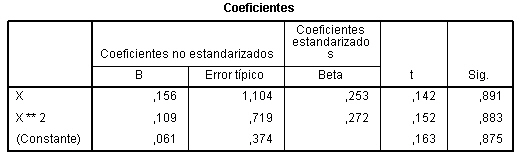
La siguiente tabla muestra las estimaciones de los parámetros del modelo de regresión lineal simple, la ordenada en el origen, \( \beta_0 = 375.252 \) y la pendiente \( \beta_1 = 0.036 \)
Por tanto, la ecuación de la recta estimada o ajustada es: y =375.252 + 0.036 x. Así mismo, en esta tabla se presentan los resultados de los dos contrastes individuales de la significación de cada uno de estos parámetros
\( \begin{array} \\ H_0 \equiv \beta_0 = 0 \\ H_1 \equiv \beta_0 \neq 0 \end{array}\)\( \hspace{1cm} \begin{array} \\ H_0 \equiv \beta_1 = 0 \\ H_1 \equiv \beta_1 \neq 0 \end{array}\)
-
El primero de estos contrastes carece de interés en la mayoría de los casos ya que raramente el punto de corte de la recta de regresión con el eje de ordenadas (ordenada en el origen) será el punto (0,0). Además dicho punto de corte carece de significado casi siempre. En nuestro caso, la interpretación de ß0 indica el valor de Y que correspondería a un valor de X igual a 0.
-
El segundo contraste, el contraste de la pendiente de la recta, es una alternativa equivalente al contraste que acabamos de comentar en la Tabla ANOVA. El estadístico de contraste que aparece en la columna t vale 4.199 tiene un p-valor asociado, columna Sig, menor que 0.001, menor que el nivel de significación \( \alpha = 0.05 \) que conduce al rechazo de la hipótesis nula y podemos afirmar que existe una relación lineal significativa entre Y y X.
Validación y diagnosis del modelo
Normalidad
El análisis de normalidad de los residuos lo realizaremos gráficamente (Histograma y gráfico de probabilidad normal) y analiticamente (Contraste de Kolmogorov-Smirnov)
Histograma
Representaremos los residuos mediante un histograma superponiendo sobre él una curva normal de media cero. Si los residuos siguen un distribución normal las barras del histograma deberán representar un aspecto similar al de dicha curva.
En primer lugar se guardan los residuos tipificados (realizado anteriormente), para ello en el Cuadro de diálogo de Analizar/Regresión/Lineal… se pulsa el botón Guardar… y en Residuos elegimos Tipificados. Clik Continuar y Aceptar.
En la ventana del Editor de datos se ha creado una variable con el nombre ZRE_1.
A continuación representamos el histograma, para ello elegimos Gráfico/Cuadros de diálogo antiguos/Histograma… y en la ventana emergente seleccionamos la variable que representa los residuos tipificados y marcamos la opción Mostrar curva normal
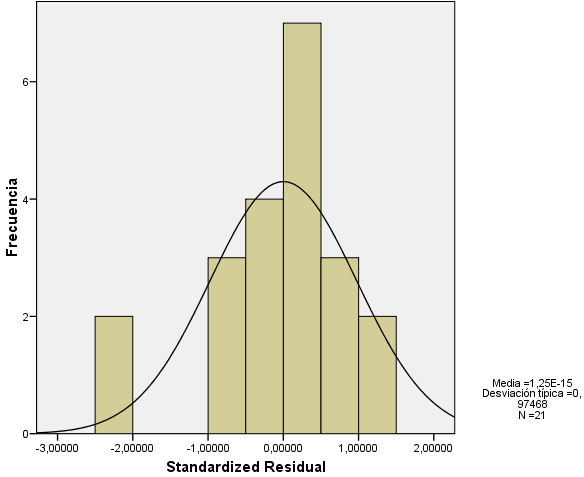
Se pulsa Continuar y Aceptar y se muestra el siguiente histograma con la curva normal superpuesta. Podemos apreciar, en este gráfico, que los datos no se aproximan razonablemente a una curva normal, puede ser consecuencia de que el tamaño muestral considerado es muy pequeño (Esta representación no es aconsejable en tamaños muestrales pequeños).
Gráfico probabilístico normal
Es el procedimiento gráfico más utilizado para comprobar la normalidad de un conjunto de datos. Para obtener dicho gráfico seleccionamos Analizar/Estadísticos descriptivos/Gráficos Q-Q… en el Cuadro de diálogo resultante se selecciona la variable que representa los residuos tipificados
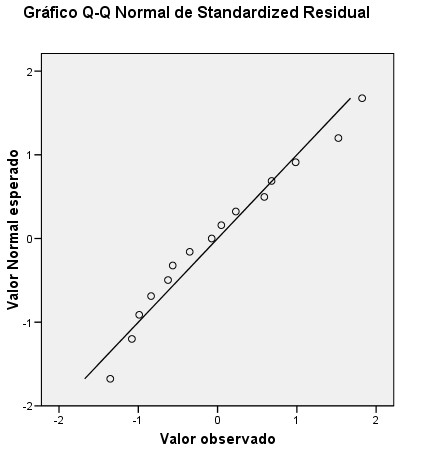
Se muestra el Gráfico siguiente que representa las funciones de distribución teórica y empírica de los residuos tipificados. En el eje de ordenadas se representa la función teórica bajo el supuesto de normalidad y en el eje de abcisas, la función empírica. Desviaciones de los puntos del gráfico respecto de la diagonal indican alteraciones de la normalidad. Observamos la ubicación de los puntos del gráfico, estos puntos se aproximan razonablemente bien a la diagonal lo que confirma la hipótesis de normalidad.
Contraste de normalidad: Prueba de Kolomogorov-Smirnov
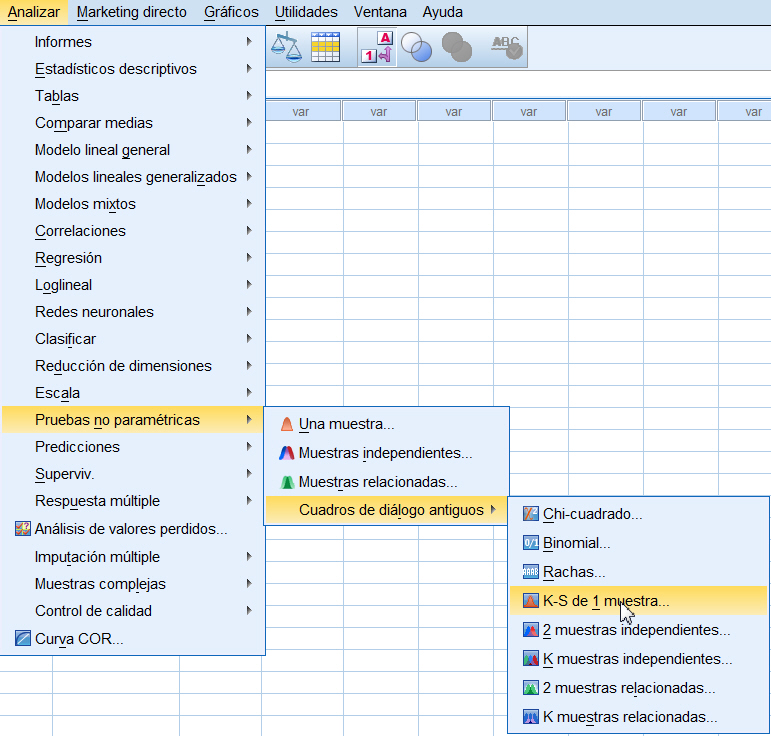
El estudio analítico de la normalidad de los residuos lo realizaremos mediante el contraste no-paramétrico de Kolmogorov-Smirnov. Seleccionamos Analizar/Pruebas no paramétricas/Cuadros de diálogos antiguos/K-S de 1 muestra…
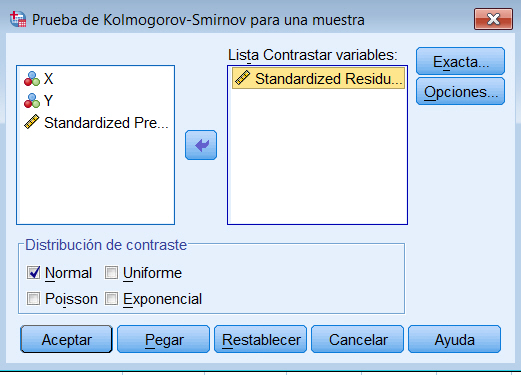
en el Cuadro de diálogo resultante se selecciona la variable que representa los residuos tipificados
La salida correspondiente la muestra la siguiente tabla
Esta tabla muestra la mayor diferencia entre los resultados esperados en caso de que los residuos surgieran de una distribución normal y los valores observados. Se distingue entre la mayor diferencia en valor absoluto, la mayor diferencia positiva y la mayor diferencia negativa. Se muestra el valor del estadístico Z (0.861) y el valor del p-valor asociado (0.448). Por lo tanto no se puede rechazar la hipótesis de normalidad de los residuos.
Homocedasticidad
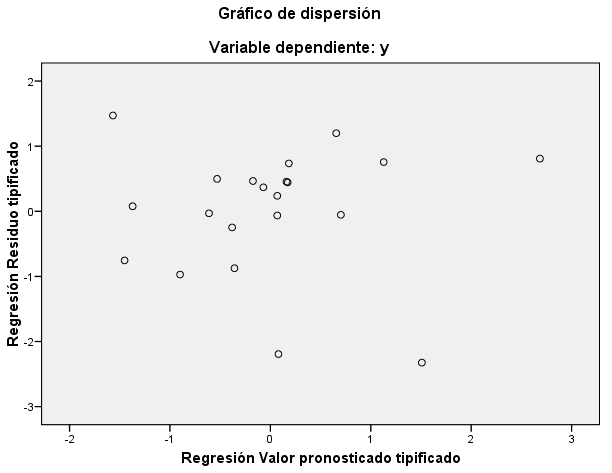
Se pulsa Continuar y Aceptar y se muestra el siguiente gráfico
Si trazamos una línea horizontal a la altura de 0, la variación de los residuos sobre esta línea, si las varianzas son iguales, debería ser semejante para los diferentes valores de Y. En el gráfico podemos observar, razonablemente, dicho comportamiento si exceptuamos algún residuo atípico que está por encima de 2. No apreciamos tendencia clara en este gráfico, los residuos no presentan estructura definida respecto de los valores predichos por el modelo por lo que no debemos rechazar la hipótesis de homocedasticidad.
Este mismo gráfico resulta muy útil para detectar indicios de falta de adecuación del modelo propuesto a los datos, posibles desviaciones de la hipótesis de linealidad. Si observamos trayectorias de comportamiento no aleatorio esto es indicio de que el modelo propuesto no describe adecuadamente los datos.
Independencia de los residuos: Contraste de Durbin-Watson
 SPSS proporciona el valor del estadístico de Durbin-Watson pero no muestra el p-valor asociado por lo que hay que utilizar las tablas correspondientes. El estadístico de Durbin-Watson mide el grado de autocorrelación entre el residuo correspondiente a cada observación y la anterior. Si su valor está próximo a 2, entonces los residuos están incorrelados, si se aproxima a 4, estarán negativamente autocorrelados y si su valor está cercano a 0 estarán positivamente autocorrelados. En nuestro caso, toma el valor 1.747, próximo a 2 lo que indica la incorrelación de los residuos.
SPSS proporciona el valor del estadístico de Durbin-Watson pero no muestra el p-valor asociado por lo que hay que utilizar las tablas correspondientes. El estadístico de Durbin-Watson mide el grado de autocorrelación entre el residuo correspondiente a cada observación y la anterior. Si su valor está próximo a 2, entonces los residuos están incorrelados, si se aproxima a 4, estarán negativamente autocorrelados y si su valor está cercano a 0 estarán positivamente autocorrelados. En nuestro caso, toma el valor 1.747, próximo a 2 lo que indica la incorrelación de los residuos.
El Diagrama de dispersión y el valor de R cuadrado (0.481), nos muestra que el ajuste lineal no es satisfactorio por lo que se deben considerar otros modelos.
Regresión Cuadrática y Correlación
se muestra la siguiente ventana
Se sitúan las variables X e Y en su campo correspondiente y se marca en Modelos la opción Cuadrático. Para incluir en el modelo el término constante (b0) se deja marcada la opción de Incluir constante en la ecuación. Si se desea obtener el gráfico de la función ajustada junto con la nube de puntos hay que dejar marcada la opción de Representar los modelos.
Se pulsa Aceptar y se obtienen las siguientes salidas
 El modelo ajustado tiene la siguiente expresión \( y = 442.883 – 0.007 x + (6.64E-006) x^2 \).
El modelo ajustado tiene la siguiente expresión \( y = 442.883 – 0.007 x + (6.64E-006) x^2 \).
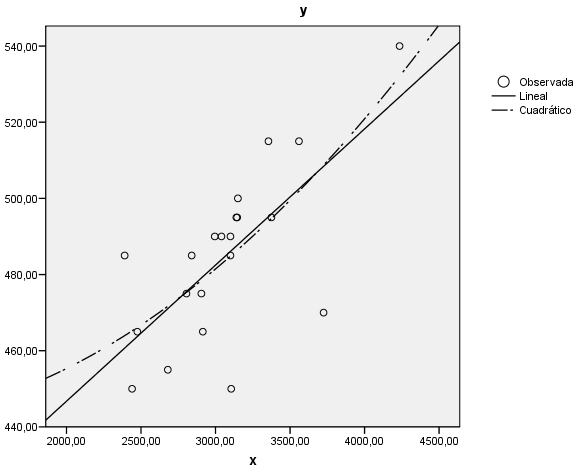
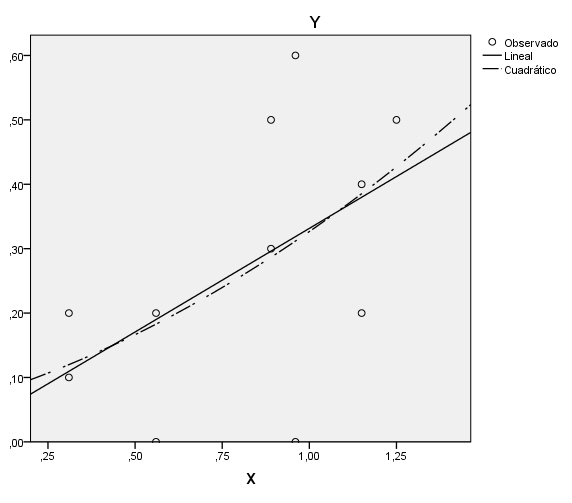
La representación gráfica de la función ajustada junto con el diagrama de dispersión es
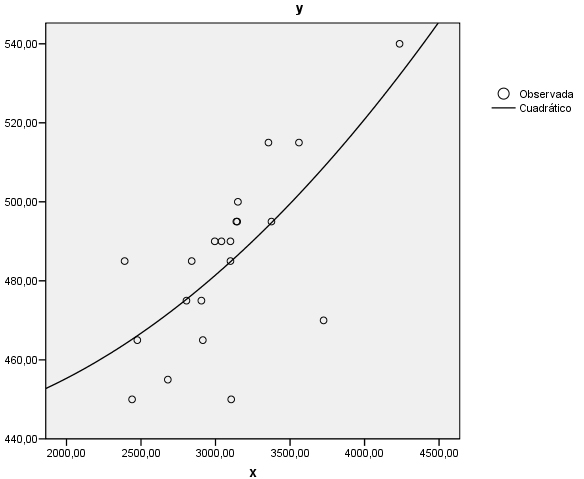 Se aprecia que la función curvilínea se ajusta moderadamente al diagrama de dispersión.
Se aprecia que la función curvilínea se ajusta moderadamente al diagrama de dispersión.
Para comparar las gráficas del ajuste lineal y del ajuste parabólico, se tienen que dejar seleccionados ambos modelos en la ventana de Estimación curvilínea. Se pulsa Aceptar y se obtienen los siguientes resultados
 La comparación del ajuste de ambos modelos se puede realizar a partir de los valores del coeficiente de determinación de cada uno de ellos, en este caso R cuadrado (lineal) = 0.481 y R cuadrado (cuadrático) = 0.488. Los resultados en el caso lineal son un poco menos satisfactorios que el cuadrático.
La comparación del ajuste de ambos modelos se puede realizar a partir de los valores del coeficiente de determinación de cada uno de ellos, en este caso R cuadrado (lineal) = 0.481 y R cuadrado (cuadrático) = 0.488. Los resultados en el caso lineal son un poco menos satisfactorios que el cuadrático.
Se aprecia, en el gráfico que el modelo cuadrático (línea discontinua) se aproxima un poco mejor a la nube de puntos que el modelo lineal (línea continua).
También podemos realizar la comparación del ajuste de los dos modelos a partir de las varianzas residuales. Para ello se debe marcar en la ventana de Estimación curvilínea la opción Mostrar tabla de ANOVA
Y se muestran los siguientes resultados:
- Para el modelo lineal
- Para el modelo cuadrático
Los resultados en el caso lineal son un poco menos satisfactorios.
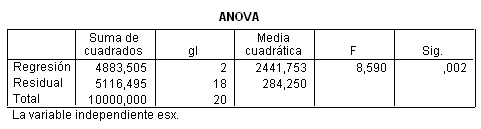 En la Tabla ANOVA se muestra un p-valor = 0.002 menor que el nivel de significación α = 0.05, por lo que se rechaza la hipótesis nula de no regresión curvilínea. Conviene puntualizar que la elección de un modelo de regresión debe tener en cuenta no sólo la bondad del ajuste numérico sino también la adecuación gráfica de los datos al mismo y, finalmente, su adecuación o explicación biológica.
En la Tabla ANOVA se muestra un p-valor = 0.002 menor que el nivel de significación α = 0.05, por lo que se rechaza la hipótesis nula de no regresión curvilínea. Conviene puntualizar que la elección de un modelo de regresión debe tener en cuenta no sólo la bondad del ajuste numérico sino también la adecuación gráfica de los datos al mismo y, finalmente, su adecuación o explicación biológica.
Ejercicios
Ejercicio Guiado
| Instalación directa de la JRE 6 para Windows Página oficial de Sun Microsystems, descarga de la JRE para cualquier plataforma |
|
Si ya tienes instalada la Máquina Virtual Java pincha en el siguiente enlace para proceder a la ejecución del ejercicio guiado
|
IMPORTANTE: Si al descargar el archivo *.JAR del ejercicio tu gestor de descargas intenta guardarlo como *.ZIP debes cambiar la extensión a .JAR para poder ejecutarlo.
Enunciado del Ejercicio
Se realiza un estudio para investigar la relación entre el nivel de humedad del suelo y la tasa de mortalidad en lombrices de tierra. La tasa de mortalidad, y, es la proporción de lombrices de tierra que mueren tras un periodo de dos semanas. El nivel de humedad, x, viene medido en milímetros de agua por centímetro cuadrado de suelo. Se obtuvieron los siguientes datos:
Se pide:
a) Diagrama de dispersión
b) Recta de regresión de la tasa de mortalidad en función del nivel de humedad. Estudiar la bondad del ajuste
c) Regresión parabólica. Estudiar la bondad del ajuste.
Ejercicios Propuestos
Ejercicio Propuesto 1
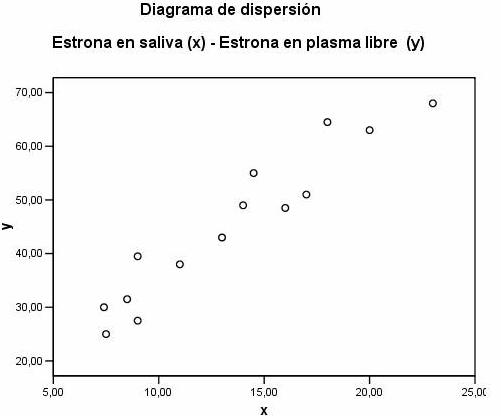
Se realiza un estudio para establecer una ecuación mediante la cual se pueda utilizar la concentración de estrona en saliva (x), para predecir la concentración de estrona en plasma libre (y). Se obtuvieron los siguientes datos de 14 hombres sanos:
Se pide:
a) Diagrama de dispersión
b) Recta de regresión de la concentración de estrona en plasma libre en función de la concentración de estrona en saliva. Estudiar la bondad del ajuste
c) Regresión parabólica. Estudiar la bondad del ajuste
d) Ajuste exponencial. ¿Qué modelo es preferible? Razona la respuesta.
Ejercicio Propuesto 2
Se realiza un estudio para investigar la relación entre el nivel de humedad del suelo y la tasa de mortalidad en lombrices. La tasa de mortalidad, Y, es la proporción de lombrices de tierra que mueren tras un periodo de dos semanas; el nivel de humedad, X, viene medido en milímetros de agua por centímetro cuadrado de suelo. Los datos se muestran en la siguiente tabla.
Se pide:
a) ¿Muestran los datos una tendencia lineal?
b) Determinar la recta de regresión Y/X, el grado de asociación lineal entre la tasa de mortalidad y el nivel de humedad y la bondad del ajuste realizado en la recta de regresión. ¿Cuánto explica el modelo?
c) Predecir el nivel de humedad del suelo si la tasa de mortalidad de las lombrices es 0.7
d) Determinar el coeficiente de correlación lineal de las rectas de regresión Y/X y X/Y
e) Ajustar los datos mediante una regresión curvilínea
d) ¿Qué ajuste es mejor? ¿Lineal? ¿Curvilíneo?
Ejercicio Propuesto 1(Resuelto)
Se realiza un estudio para establecer una ecuación mediante la cual se pueda utilizar la concentración de estrona en saliva (x), para predecir la concentración de estrona en plasma libre (y). Se obtuvieron los siguientes datos de 14 hombres sanos:
Se pide:
a) Diagrama de dispersión
b) Recta de regresión de la concentración de estrona en plasma libre en función de la concentración de estrona en saliva. Estudiar la bondad del ajuste
c) Regresión parabólica. Estudiar la bondad del ajuste
d) Ajuste exponencial. ¿Qué modelo es preferible? Razona la respuesta.
Solución:
a) Diagrama de Dispersión
b) Recta de regresión de la concentración de estrona en plasma libre en función de la concentración de estrona en saliva. Estudiar la bondad del ajuste.
-
El coeficiente de correlación lineal de Pearson (R) es igual a 0.954 y el coeficiente de determinación, R cuadrado, es igual a 0.911. Este valor indica que el 91.1% de la variabilidad de la concentración de estrona en plasma es explicada por el modelo propuesto. El grado de ajuste es alto.
-
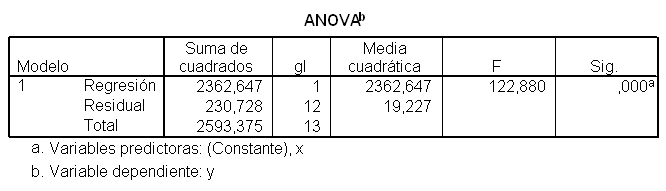
La Tabla ANOVA muestra un valor del estadístico F = 122.880 y un p-valor asociado menor que 0.001, lo que conduce a rechazar la hipótesis nula de no linealidad. Por tanto, existe una relación lineal significativa entre Y y X
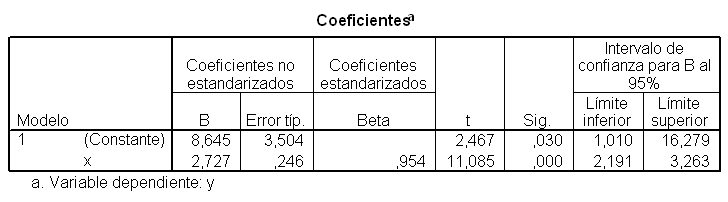
- La Tabla de los Coeficientes muestra:
-
Las estimaciones de los parámetros del modelo de regresión lineal simple, la ordenada en el origen, ß0=8.645 y la pendiente ß1= 2.727. Por lo tanto, la ecuación de la recta estimada o ajustada es: y = 8.645 + 2.727 x
-
El contraste de la pendiente de la recta que es una alternativa equivalente al contraste que acabamos de comentar en la Tabla ANOVA. El estadístico de contraste que aparece en la columna t vale 11.085 tiene un p-valor asociado, columna Sig, menor que 0.001, menor que el nivel de significación 0.05 que conduce al rechazo de la hipótesis nula y podemos afirmar que existe una relación lineal significativa entre Y y X. En la última columna de la tabla se muestran los intervalos de confianza para ß0 y ß1, al 95%. El intevalo para ß1 es (2.191, 3.263), puesto que el cero no pertenece al intervalo, hay evidencia empírica para concluir que X influye en Y y por tanto al nivel de confianza del 95% el parámetro ß1 no podría considerarse igual a cero.
-
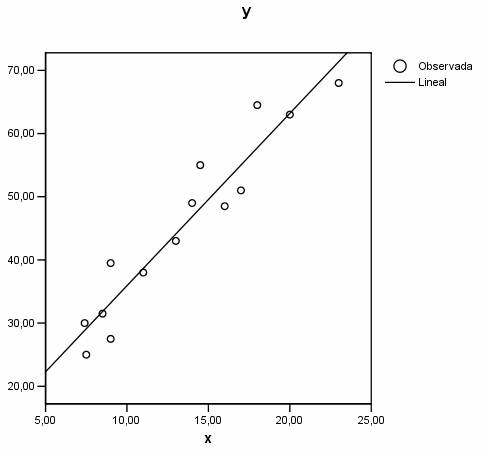
El gráfico muestra un buen ajuste lineal y una tendencia creciente.
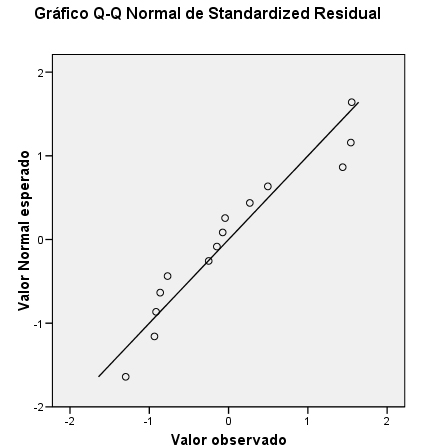
Este gráfico representa las funciones de distribución teórica y empírica de los residuos tipificados. En el eje de ordenadas se representa la función teórica bajo el supuesto de normalidad y en el eje de abcisas, la función empírica. Desviaciones de los puntos del gráfico respecto de la diagonal indican alteraciones de la normalidad. Observamos la ubicación de los puntos del gráfico, estos puntos se aproximan razonablemente a la diagonal lo que puede confirmar la hipótesis de normalidad. A continuación vamos a realizar el estudio analítico de la normalidad de los residuos mediante el contraste no-paramétrico de Kolmogorov-Smirnov.
 Esta tabla muestra la mayor diferencia entre los resultados esperados en caso de que los residuos surgieran de una distribución normal y los valores observados. Se distingue entre la mayor diferencia en valor absoluto, la mayor diferencia positiva y la mayor diferencia negativa. Se muestra el valor del estadístico Z (0.603) y el valor del p-valor asociado (0.861). Por lo tanto no se puede rechazar la hipótesis de normalidad de los residuos.
Esta tabla muestra la mayor diferencia entre los resultados esperados en caso de que los residuos surgieran de una distribución normal y los valores observados. Se distingue entre la mayor diferencia en valor absoluto, la mayor diferencia positiva y la mayor diferencia negativa. Se muestra el valor del estadístico Z (0.603) y el valor del p-valor asociado (0.861). Por lo tanto no se puede rechazar la hipótesis de normalidad de los residuos.
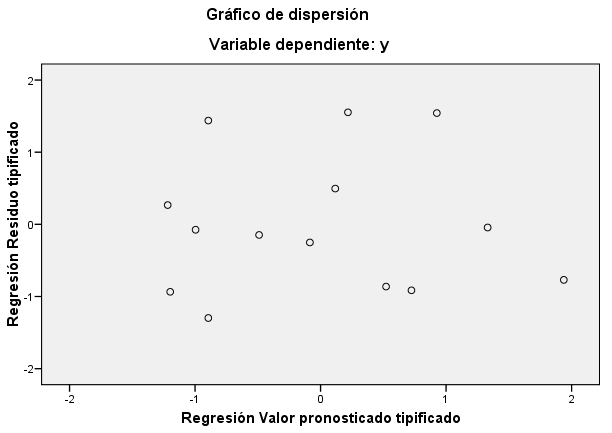
La homocedasticidad de las varianzas la comprobamos gráficamente: Para ello representamos los residuos tipificados frente a los valores de y estimados tipificados. El análisis de este gráfico puede revelar una posible violación de la hipótesis de homocedasticidad, por ejemplo si detectamos que el tamaño de los residuos aumenta o disminuye de forma sistemática para algunos valores ajustados de la variable Y, si observamos que el gráfico muestra forma de embudo… Si por el contario dicho gráfico no muestra patrón alguno, entonces no podemos rechazar la hipótesis de igualdad de varianzas.
No apreciamos tendencia clara en este gráfico, los residuos no presentan estructura definida respecto de los valores predichos por el modelo por lo que no debemos rechazar la hipótesis de homocedasticidad.
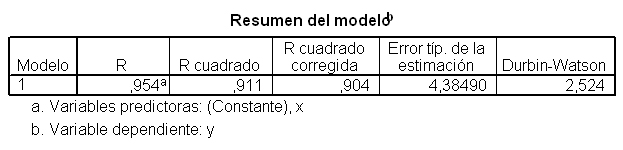 La hipótesis de independencia de los residuos la realizamos mediante el contraste de Durbin-Watson. El estadístico de Durbin-Watson mide el grado de autocorrelación entre el residuo correspondiente a cada observación y la anterior. Si su valor está próximo a 2, entonces los residuos están incorrelados, si se aproxima a 4, estarán negativamente autocorrelados y si su valor está cercano a 0 estarán positivamente autocorrelados. En nuestro caso, toma el valor 2.524,
La hipótesis de independencia de los residuos la realizamos mediante el contraste de Durbin-Watson. El estadístico de Durbin-Watson mide el grado de autocorrelación entre el residuo correspondiente a cada observación y la anterior. Si su valor está próximo a 2, entonces los residuos están incorrelados, si se aproxima a 4, estarán negativamente autocorrelados y si su valor está cercano a 0 estarán positivamente autocorrelados. En nuestro caso, toma el valor 2.524,
próximo a 2 lo que indica la incorrelación de los residuos.
c) Regresión parabólica. Estudiar la bondad del ajuste
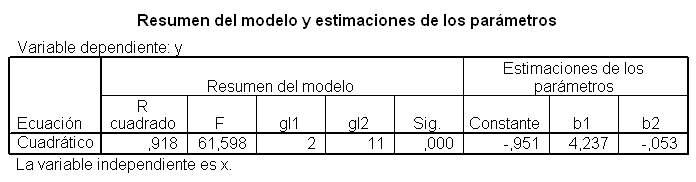 El modelo ajustado tiene la siguiente expresión: y = -0.951 + 4.237 x – 0.053 x^2
El modelo ajustado tiene la siguiente expresión: y = -0.951 + 4.237 x – 0.053 x^2
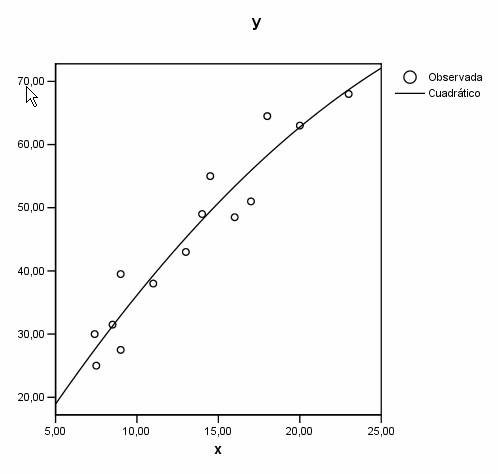
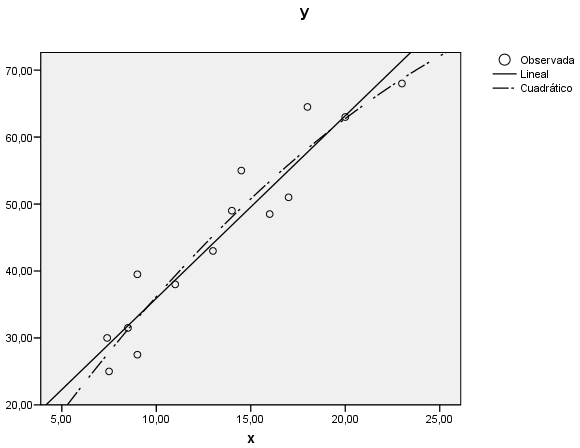
La representación gráfica de la función ajustada junto con la nube de puntos es
Se aprecia que la función curvilínea se ajusta moderadamente al diagrama de dispersión.
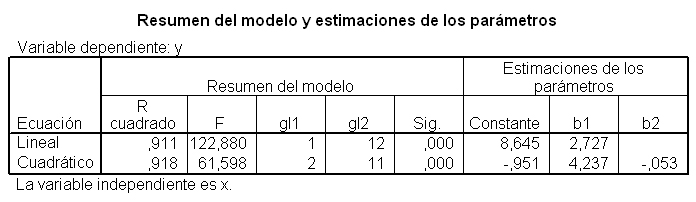
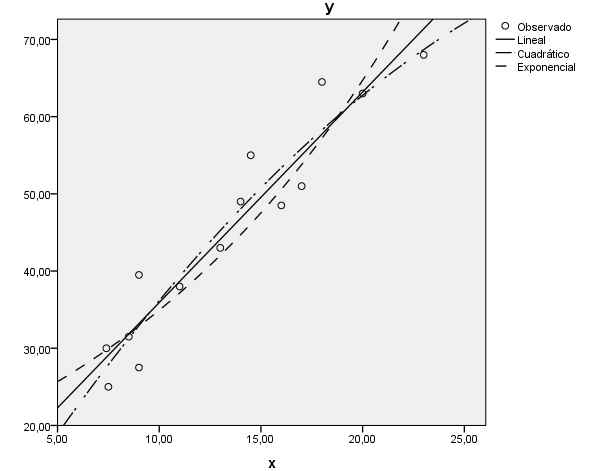
La comparación del ajuste de ambos modelos se puede realizar a partir de los valores del coeficiente de determinación de cada uno de ellos, en este caso R cuadrado (lineal) = 0.911 y R cuadrado (cuadrático) = 0.918. Los resultados en el caso lineal son un poco menos satisfactorios que el cuadrático.
Se aprecia, en el gráfico que el modelo cuadrático (línea discontinua) se aproxima un poco mejor a la nube de puntos que el modelo lineal (línea continua).
También podemos realizar la comparación del ajuste de los dos modelos a partir de las varianzas residuales. Para ello se debe marcar en la ventana de Estimación curvilínea la opción Mostrar tabla de ANOVA
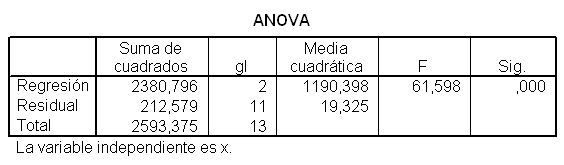 En la tabla ANOVA se muestra un p-valor menor que 0.001 menor que el nivel de significación 0.05, por lo que se rechaza la hipótesis nula de no regresión curvilínea.
En la tabla ANOVA se muestra un p-valor menor que 0.001 menor que el nivel de significación 0.05, por lo que se rechaza la hipótesis nula de no regresión curvilínea.
Los valores obtenidos de los coeficientes de determinación son: R cuadrado (lineal) = 0.911 y R cuadrado (cuadrático) = 0.918, puesto que la diferencia entre ambos coeficientes es muy pequeña, se considerará el modelo lineal por su simplicidad.
Conviene puntualizar que la elección de un modelo de regresión debe tener en cuenta no sólo la bondad del ajuste numérico sino también la adecuación gráfica de los datos al mismo y, finalmente, su adecuación o explicación biológica.
d) Ajuste exponencial. ¿Qué modelo es preferible? Razona la respuesta.
Para realizar un ajuste exponencial se selecciona, en el menú principal, Analizar/ Regresión /Estimación curvilínea.
Se muestra la siguiente ventana
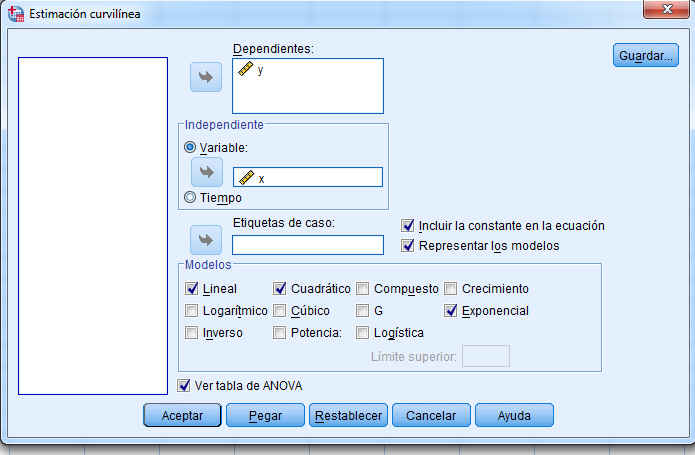
Se introducen las variables en sus respectivos campos y se selecciona Exponencial, Cuadrático y Ver tabla de ANOVA. Se pulsa Aceptar y se muestran las siguientes salidas:
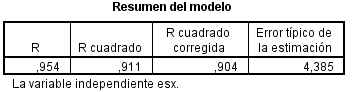
AJUSTE LINEAL
-
El coeficiente de determinación, R cuadrado, es igual a 0.911. Este valor indica que el 91.1% de la variabilidad de la concentración de estrona en plasma es explicada por el modelo propuesto. El grado de ajuste es alto.
-
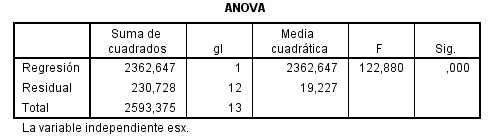
La Tabla ANOVA muestra un valor del estadístico F = 122.880 y un p-valor asociado menor que 0.001, lo que conduce a rechazar la hipótesis nula de no linealidad. Por tanto, existe una relación lineal significativa entre Y y X
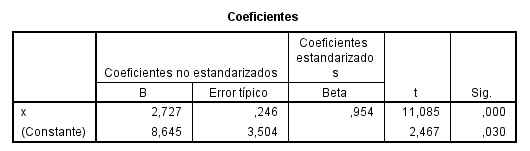
- La Tabla de los Coeficientes muestra:
-
Las estimaciones de los parámetros del modelo de regresión lineal simple, la ordenada en el origen, ß0=8.645 y la pendiente ß1= 2.727. Por lo tanto, la ecuación de la recta estimada o ajustada es: y = 8.645 + 2.727 x
-
AJUSTE CUADRÁTICO
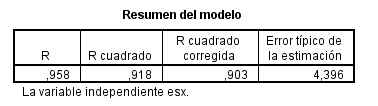
El coeficiente de determinación correspondiente R cuadrado (cuadrático) = 0.918
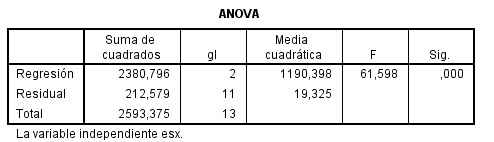
En la tabla ANOVA se muestra un p-valor menor que 0.001 menor que el nivel de significación 0.05, por lo que se rechaza la hipótesis nula de no regresión curvilínea
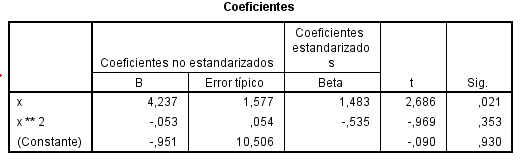
El modelo ajustado tiene la siguiente expresión: y = -0.951 + 4.237 x – 0.053 x^2
AJUSTE EXPONENCIAL
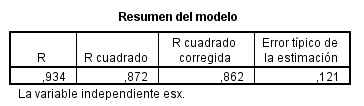
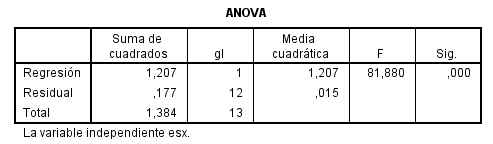
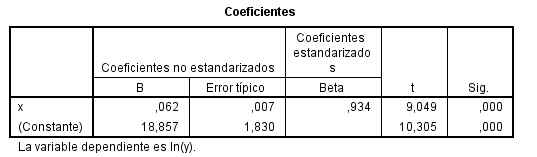
El coeficiente de determinación correspondiente R cuadrado (cuadrático) = 0.872
En la tabla ANOVA se muestra un p-valor menor que 0.001 menor que el nivel de significación 0.05, por lo que se rechaza la hipótesis nula de no regresión exponencial
El modelo ajustado tiene la siguiente expresión: ln (y) = ln (18.857) + x ln (0.062).
Los tres modelos son válidos y pueden ser empleados para obtener predicciones de la concentración de estrona en plasma libre en función de la concentración de estrona en saliva. Sin embargo el coeficiente de determinación correspondiente al modelo cuadrático es igual a 0,918, superior a 0,911 correspondiente al modelo lineal y a 0.872 correspondiente al modelo exponencial. Por tanto, es preferible utilizar el modelo cuadrático
 .
.
Ejercicio Propuesto 2 (Resuelto)
Se realiza un estudio para investigar la relación entre el nivel de humedad del suelo y la tasa de mortalidad en lombrices. La tasa de mortalidad, Y, es la proporción de lombrices de tierra que mueren tras un periodo de dos semanas; el nivel de humedad, X, viene medido en milímetros de agua por centímetro cuadrado de suelo. Los datos se muestran en la siguiente tabla.
Se pide:
a) ¿Muestran los datos una tendencia lineal?
b) Determinar la recta de regresión Y/X, el grado de asociación lineal entre la tasa de mortalidad y el nivel de humedad y la bondad del ajuste realizado en la recta de regresión. ¿Cuánto explica el modelo?
c) Predecir el nivel de humedad del suelo si la tasa de mortalidad de las lombrices es 0.7
d) Determinar el coeficiente de correlación lineal de las rectas de regresión Y/X y X/Y
e) Ajustar los datos mediante una regresión curvilínea
d) ¿Qué ajuste es mejor? ¿Lineal? ¿Curvilíneo?
Solución:
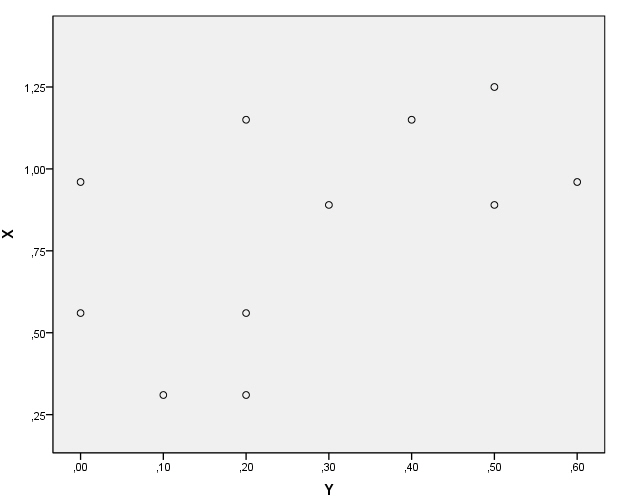
a) ¿Muestran los datos una tendencia lineal?
b) Determinar la recta de regresión Y/X, el grado de asociación lineal entre la tasa de mortalidad y el nivel de humedad y la bondad del ajuste realizado en la recta de regresión. ¿Cuánto explica el modelo?
c) Predecir el nivel de humedad del suelo si la tasa de mortalidad de las lombrices es 0.7
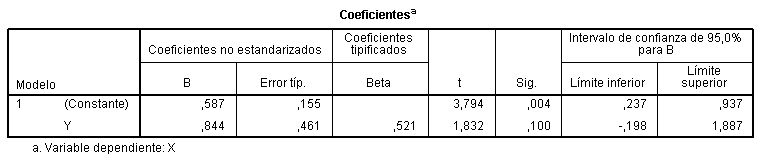
Para resolverlo es necesario determinar la recta de regresión X/Y
Para una tasa de mortalidad de 0.7, el nivel de humedad del suelo es 1.1778
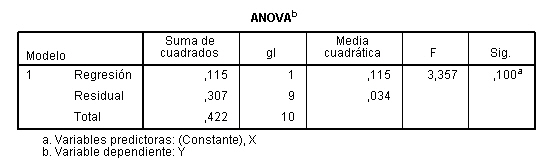
d) Determinar el coeficiente de correlación lineal de las rectas de regresión Y/X y X/Y : r = 0.521
e) Ajustar los datos mediante una regresión curvilínea
d) ¿Qué ajuste es mejor? ¿Lineal? ¿Curvilíneo?
Ajuste lineal
.
APÉNDICE: Regresión múltiple
El modelo de regresión múltiple es la extensión a k variables explicativas del modelo de regresión simple estudiado en el apartado anterior. En general, una variable de interés y depende de varias variables x1, x2,…, xk, y no sólo de una única variable de predicción x.
Por ejemplo, para estudiar la variación del precio de una vivienda, parece razonable considerar más de una variable explicativa, como pueden ser el precio del suelo, la superficie del piso, el número de cuartos de baño, la edad de la vivienda, etc. Además de las variables observables, la variable de interés puede depender de otras desconocidas para el investigador, que pueden ser controlables o no. Un modelo de regresión representa tanto el efecto de las variables observables como de estas otras variables que reciben el nombre de error aleatorio o perturbación.
Si suponemos un modelo de regresión teórico en el que las variables se pueden relacionar mediante una función de tipo lineal, éste puede escribirse
donde:
- ß1, ß2,…, ßk son los parámetros desconocidos que vamos a estimar
- ε es el error aleatorio o perturbación, que representa el efecto de todas las variables que pueden afectar a la variable dependiente y no están incluidas en el modelo de regresión
- y es la variable de interés que queremos predecir, también llamada variable respuesta o variable dependiente
- x1, x2,…, xk reciben el nombre de variables independientes, explicativas o de predicción.
Ejemplos de modelos de regresión múltiple:
- El consumo de combustible de un vehículo, cuya variación puede ser explicada por la velocidad media del mismo y por el tipo de carretera. Podemos incluir en el término de error, variables como el efecto del conductor, las condiciones meteorológicas, etc.
- El presupuesto de una universidad, cuya variación puede ser explicada por el número de alumnos. También podríamos considerar en el modelo variables como el número de profesores, el número de laboratorios, la superficie disponible de instalaciones, personal de administración, etc.
Si se desea explicar los valores de una variable aleatoria y, mediante k variables, que a su vez toman n valores, tenemos entonces
Las perturbaciones o errores aleaotorios deben verificar las siguientes hipótesis:
- Su esperanza es cero
- Su varianza es constante
- Son independientes entre sí
- Su distribución es normal
Los parámetros desconocidos, ß1, ß2,…, ßk se estiman mediante el método de mínimos cuadrados, resultando la ecuación estimada de regresión dada por
![]()
Fórmula 4: Ecuación de regresión estimada
donde
- cada coeficiente
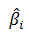 representa el efecto sobre la variable respuesta, y, cuando la variable aumenta en una unidad y las demás variables permanecen constantes. Puede interpretarse como el efecto diferencial de esta variable sobre la variable respuesta cuando controlamos los efectos de las otras variables.
representa el efecto sobre la variable respuesta, y, cuando la variable aumenta en una unidad y las demás variables permanecen constantes. Puede interpretarse como el efecto diferencial de esta variable sobre la variable respuesta cuando controlamos los efectos de las otras variables. 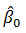 es el valor de la variable respuesta ajustada cuando todas las variables explicativas toman el valor cero.
es el valor de la variable respuesta ajustada cuando todas las variables explicativas toman el valor cero.
Supuesto Práctico
Una empresa fabricante de cereales para el desayuno desea conocer la ecuación que permita predecir las ventas (en miles de euros) en función de los gastos en publicidad infantil en televisión (en miles de euros), la inversión en publicidad en radio (en miles de euros) y la inversión en publicidad en los periódicos (en miles de euros). Se realiza un estudio en el que se reúnen los datos mensuales correspondientes a los últimos 20 meses. Estos datos se muestran en la siguiente tabla
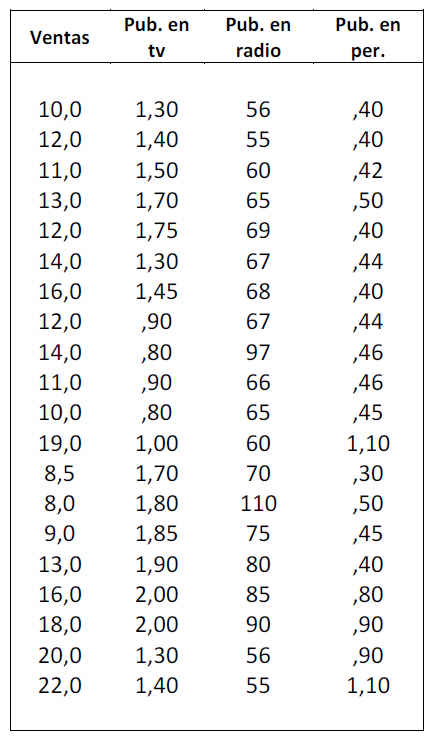
Se pide:
- Ajustar un modelo de regresión lineal múltiple. Obtener una estimación de los parámetros del modelo y su interpretación
- Contrastar la significación del modelo propuesto
- ¿Puede eliminarse alguna variable del modelo? Realiza los contrastes de significación individuales
- Coeficiente de determinación y de determinación corregido
Solución
- Ajustar un modelo de regresión lineal múltiple. Obtener una estimación de los parámetros del modelo y su interpretación
Las variables que intervienen en el ejercicio la hemos notado por: Ventas, Pub_tv, Pub_rad y Pub_per
- Ventas: Es la variable dependiente
- Pub_tv, Pub_rad y Pub_per: Son las variables explicativas.
Introducimos dichas variables en la Vista de Variables de SPSS, como se muestra

El modelo de regresión que vamos a ajustar responde a una expresión deltipo:
- y representa las ventas de cereales (en miles de euros)
- x1 es el coste de la publicidad en televisión (en miles de euros)
- x2 es el coste de la publicidad en radio (en miles de euros)
- x3 es el coste de la publicidad en periódicos (en miles de euros).
Los parámetros desconocidos β1, β2 y β3 se estiman por el método de mínimos cuadrados.
La ecuación estimada de regresión está dada por:
- Cada coeficiente
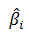 (i=1,2,3), representa el cambio sobre la variable respuesta estimada, y, para un aumento igual a una unidad de la correspondiente variable xi cuando la variable aumenta en una unidad y las demás variables permanecen constantes. Puede interpretarse como el efecto diferencial de esta variable sobre la variable respuesta cuando controlamos los efectos de las otras variables.
(i=1,2,3), representa el cambio sobre la variable respuesta estimada, y, para un aumento igual a una unidad de la correspondiente variable xi cuando la variable aumenta en una unidad y las demás variables permanecen constantes. Puede interpretarse como el efecto diferencial de esta variable sobre la variable respuesta cuando controlamos los efectos de las otras variables. 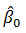 es el valor de la variable respuesta ajustada cuando todas las variables predictivas toman el valor cero.
es el valor de la variable respuesta ajustada cuando todas las variables predictivas toman el valor cero.
Para realizar el análisis de regresión mediante el paquete SPSS seleccionamos en el menú principal: Analizar/Regresión/Lineales.
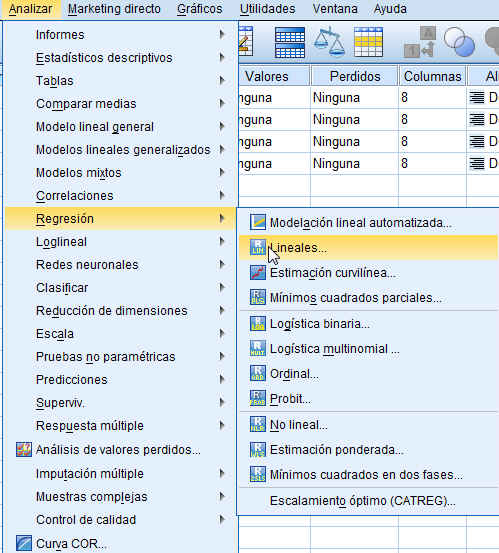
En la ventana correspondiente, se introducen las tres variables explicativas en el campo Variables Independientes y la variable Ventas en el campo Variable Dependiente, como muestra la siguiente figura.
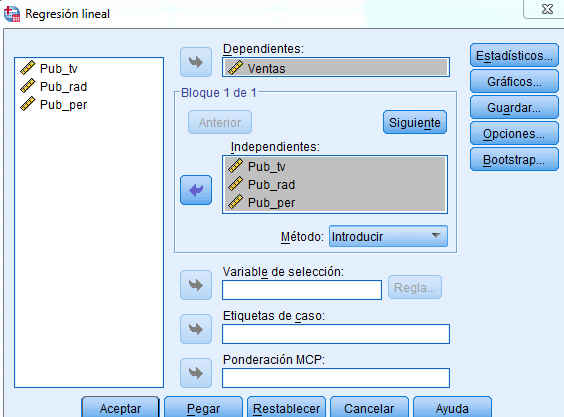
Se pulsa Aceptar y se obtiene como resultado la siguiente salida del programa
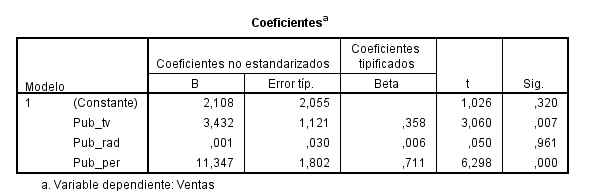
La tabla de Coeficientes muestra los parámetros estimados de regresión \( \hat{\beta}_{0} \), \( \hat{\beta}_{i} (i=1,2,3) \), cuyos valores son 2.108, 3.432 , 0.001 y 11.347, respectivamente
La ecuación de regresión ajustada está dada por:
\( Ventas_i = 2.108 + 3.432 PubTVi + 0.001 PubRadio_i + 11.347 PubPrensa_i \)
Expresión del modelo pedido
- Las ventas estimadas son iguales a 2108 euros si no se produce inversión en publicidad (ni en televisión, ni en radio ni en periódicos).
- Por cada mil euros invertidos en publicidad en televisión las ventas esperadas aumentan en 3432 euros, supuesto que permanecen constantes las otras variables.
- Por cada mil euros invertidos en publicidad en radio, las ventas estimadas aumentan únicamente en 1 euro, suponiendo que se mantienen constantes las otras variables independientes.
- Por cada mil euros invertidos en publicidad en periódicos se produce un incremento en las ventas esperadas de 11347 euros, supuestas constantes las restantes variables predictivas.
A la vista de estos resultados parece recomendable la inversión en publicidad en periódicos frente a la publicidad en televisión o en radio.
2. Contrastar la significación del modelo propuesto
El contraste de significación del modelo de regresión permite verificar si ninguna variable explicativa es válida para la predicción de la variable de interés.
Este contraste puede escribirse
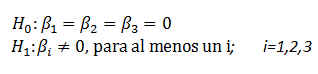 Expresión del contraste pedido
Expresión del contraste pedido
El p-valor asociado a este contraste se muestra en la tabla ANOVA:
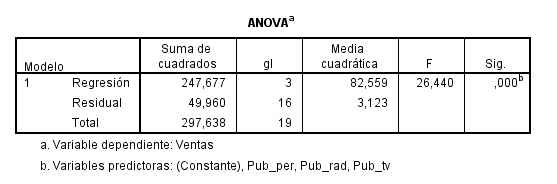
El p-valor asociado al contraste es menor que 0.001, (Sig = 0.000), por lo que rechazamos la hipótesis nula. Esto implica que al menos una de las variables independientes contribuye de forma significativa a la explicación de la variable respuesta.
3. ¿Puede eliminarse alguna variable del modelo? Realiza los contrastes de significación individuales
En la salida de SPSS correspondiente a la tabla de coeficientes se muestran los p-valores asociados a los contrastes de regresión individuales

Realizamos tres contrastes de hipótesis, uno para cada coeficiente que acompaña a cada variable explicativa ( i = 1, 2,3)
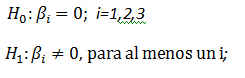 Expresión del contraste pedido
Expresión del contraste pedido
Para la variable Publ_radio, p-valor = 0.961 > α = 0.05, por lo que no rechazamos la hipótesis nula de significación de la variable Publ_radio. Esta variable no es válida para predecir las ventas de cereales y por tanto puede ser eliminada del modelo.
4. Coeficiente de determinación y de determinación corregido
El Coeficiente de determinación es una medida descriptiva del ajuste global de un modelo de regresión, dado por
Este coeficiente representa la proporción de variación de y explicada por el modelo de regresión. Por construcción, es evidente que 0 ≤ R2 ≤1
- Si R2 = 1, entonces SCReg = SCT, por lo que toda la variación de y es explicada por el modelo de regresión
- Si R2 = 0, entonces SCR=SCT, por lo que toda la variación de y queda sin explicar.
En general, cuanto más próximo esté a 1, mayor es la variación de y explicada por el modelo de regresión.
Sin embargo, en regresión múltiple, el coeficiente de determinación presenta el inconveniente de que su valor aumenta al añadir nuevas variables al modelo de regresión, independientemente de que éstas contribuyan de forma significativa a la explicación de la variable respuesta. Para evitar un aumento injustificado de este coeficiente, se introduce el coeficiente de determinación corregido, que notamos por![]() y que se obtiene a partir de R2 de la siguiente forma
y que se obtiene a partir de R2 de la siguiente forma
Este coeficiente no aumenta su valor cuando se añaden nuevas variables, sino que en caso de añadir variables superfluas al modelo, el valor de![]() disminuye considerablemente respecto al valor del coeficiente R2.
disminuye considerablemente respecto al valor del coeficiente R2.
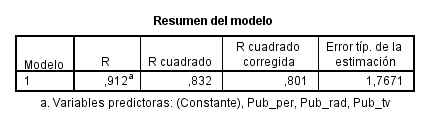
El coeficiente de determinación es igual a 0.832 y el coeficiente de determinación corregido es igual a 0,801. En este caso no se aprecian grandes diferencias entre los dos coeficientes . El 83.2 % de la variación en las ventas de cereales se explican por su relación lineal con el modelo propuesto. El valor del coeficiente de determinación es satisfactorio.
Ejercicios Propuestos
Ejercicio Propuesto 3
Dada la cantidad de gasolina en porcentaje con respecto a la cantidad del petróleo en crudo, denotada por y. Se quiere saber si se puede expresar como combinación lineal de cuatro variables: la gravedad del crudo, la presión del vapor del crudo, la temperatura para la cual se ha evaporado un 10% y la temperatura para la cual se ha evaporado el 100%, a partir de los siguientes datos:
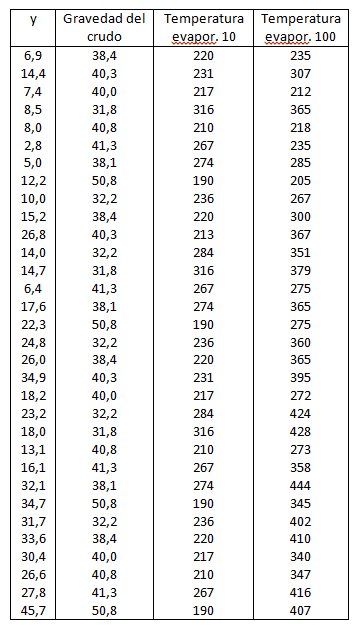 Tabla de datos del ejercicio propuesto 3
Tabla de datos del ejercicio propuesto 3
Se pide:
- Ajustar un modelo de regresión lineal múltiple. Obtener una estimación de los parámetros del modelo y su interpretación
- Contrastar la significación del modelo propuesto
- ¿Puede eliminarse alguna variable del modelo? Realiza los contrastes de significación individuales
- Coeficiente de determinación y de determinación corregido.
Ejercicio Propuesto 4
Se pretende estudiar la posible relación lineal entre el precio de pisos en miles de euros, en una conocida ciudad española y variables como la superficie en m2 y la antigüedad del inmueble en años. Para ello, se realiza un estudio, en el que se selecciona de forma aleatoria una muestra estratificada representativa de los distintos barrios de la ciudad. Los datos aparecen en la siguiente tabla.
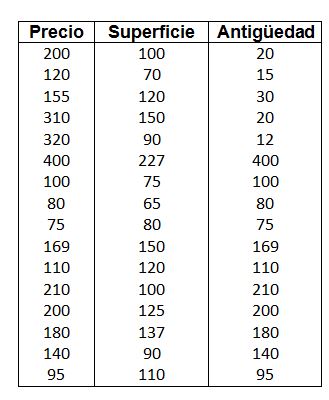 Datos del Ejercicio Propuesto 4
Datos del Ejercicio Propuesto 4
Se pide:
- Ajustar un modelo de regresión lineal múltiple. Obtener una estimación de los parámetros del modelo y su interpretación
- Contrastar la significación del modelo propuesto
- ¿Cuánto será el precio estimado del piso en una conocida ciudad española para una superficie en 130 m2 y 35 años de antigüedad?
- ¿Puede eliminarse alguna variable del modelo? Razona la respuesta
- Coeficiente de determinación y de determinación corregido. Interpretación.
Ejercicio Propuesto 3 (Resuelto)
Dada la cantidad de gasolina en porcentaje con respecto a la cantidad del petróleo en crudo, denotada por y. Se quiere saber si se puede expresar como combinación lineal de cuatro variables: la gravedad del crudo, la presión del vapor del crudo, la temperatura para la cual se ha evaporado un 10% y la temperatura para la cual se ha evaporado el 100%, a partir de los siguientes datos:
 Tabla de datos del ejercicio propuesto 3
Tabla de datos del ejercicio propuesto 3
Se pide:
- Ajustar un modelo de regresión lineal múltiple. Obtener una estimación de los parámetros del modelo y su interpretación
- Contrastar la significación del modelo propuesto
- ¿Puede eliminarse alguna variable del modelo? Realiza los contrastes de significación individuales
- Coeficiente de determinación y de determinación corregido.
Solución:
- Ajustar un modelo de regresión lineal múltiple. Obtener una estimación de los parámetros del modelo y su interpretación
Se introducen los datos en el editor de datos y se selecciona, en el menú principal, Analizar/Regresión/Lineales. En la ventana resultante se introducen las variables
Se pulsa Aceptar y se obtienen las siguientes salidas
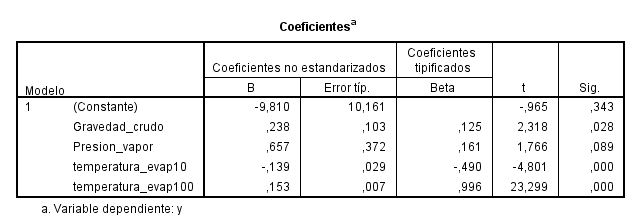
En la tabla de coeficientes figuran los parámetros estimados del modelo de regresión. Por lo tanto, la ecuación de regresión ajustada está dada por:
yˆ = -9.810 + 0.238x1 + 0.657x2 – 0.139x3 +0.153 x4
- La cantidad de gasolina estimada disminuye en 9.810 si no se produce gravedad en crudo, ni presión del vapor en crudo, ni temperatura de evaporación de un 10%, ni temperatura de evaporación de un 100%.
- Por cada unidad de gravedad en crudo la cantidad de gasolina esperada aumenta en 0.238, supuesto que permanecen constantes las otras variables.
- Por cada unidad de presión del vapor en crudo, la cantidad de gasolina esperada aumenta en 0.657, supuesto que permanecen constantes las otras variables.
- Por cada unidad de temperatura de evaporación de un 10%, la cantidad de gasolina esperada disminuye en 0.139, supuesto que permanecen constantes las otras variables
- Por cada unidad de temperatura de evaporación de un 100%, la cantidad de gasolina esperada aumenta en 0.153, supuestas constantes las restantes variables predictivas.
A la vista de estos resultados parece recomendable que la cantidad de gasolina en porcentaje con respecto a la cantidad del petróleo en crudo se exprese en función de la presión del vapor del crudo frente a las restantes variables predictivas. A pesar de que este valor es el mayor veremos en el apartado 3º que esta variable no es significativa.
2. Contrastar la significación del modelo propuesto.
El contraste de significación del modelo de regresión permite verificar si ninguna variable explicativa es válida para la predicción de la variable de interés.
Este contraste puede escribirse
Expresión del contraste pedidio
El p-valor asociado a este contraste se muestra en la tabla ANOVA:
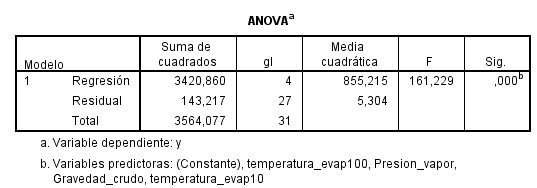 El p-valor asociado al contraste es menor que 0.001, (Sig = 0.000), por lo que rechazamos la hipótesis nula. Esto implica que al menos una de las variables independientes contribuye de forma significativa a la explicación de la variable respuesta.
El p-valor asociado al contraste es menor que 0.001, (Sig = 0.000), por lo que rechazamos la hipótesis nula. Esto implica que al menos una de las variables independientes contribuye de forma significativa a la explicación de la variable respuesta.
3. ¿Puede eliminarse alguna variable del modelo? Realiza los contrastes de significación individuales
En la salida de SPSS correspondiente a la tabla de coeficientes se muestran los p-valores asociados a los contrastes de regresión individual.

Realizamos cuatro contrastes de hipótesis, uno para cada coeficiente que acompaña a cada variable explicativa ( i = 1, 2,3,4 )
Para la variable Presión_vapor, p-valor = 0.089 > α = 0.05, por lo que no rechazamos la hipótesis nula de significación de la variable presión del vapor en crudo. Esta variable no es válida para predecir la cantidad de gasolina y por tanto puede ser eliminada del modelo.
Por lo tanto, en el apartado 1º, la respuesta debe ser la variable Gravedad_crudo ya que es el siguiente valor más grande del coeficiente y es significativamente distinta de cero. A la vista de estos resultados parece recomendable que la cantidad de gasolina en porcentaje con respecto a la cantidad del petróleo en crudo se exprese en función de la Gravedad en crudo frente a las restantes variables predictivas.
4. Coeficiente de determinación y de determinación corregido
El coeficiente de determinación es igual a 0.960 y el coeficiente de determinación corregido es igual a 0,954. En este caso no se aprecian grandes diferencias entre los dos coeficientes. El 96 % de la variación de la cantidad de gasolina se explica por su relación lineal con el modelo propuesto. El valor del coeficiente de determinación es satisfactorio.
Ejercicio Propuesto 4 (Resuelto)
Se pretende estudiar la posible relación lineal entre el precio de pisos en miles de euros, en una conocida ciudad española y variables como la superficie en m2 y la antigüedad del inmueble en años. Para ello, se realiza un estudio, en el que se selecciona de forma aleatoria una muestra estratificada representativa de los distintos barrios de la ciudad. Los datos aparecen en la siguiente tabla.
 Datos del Ejercicio Propuesto 4
Datos del Ejercicio Propuesto 4
Se pide:
- Ajustar un modelo de regresión lineal múltiple. Obtener una estimación de los parámetros del modelo y su interpretación
- Contrastar la significación del modelo propuesto
- ¿Cuánto será el precio estimado del piso en una conocidad ciudad española para una superficie en 130 m2 y 35 años de antigüedad?
- ¿Puede eliminarse alguna variable del modelo? Razona la respuesta
- Coeficiente de determinación y de determinación corregido. Interpretación.
Solución:
1. Ajustar un modelo de regresión lineal múltiple. Obtener una estimación de los parámetros del modelo y su interpretación
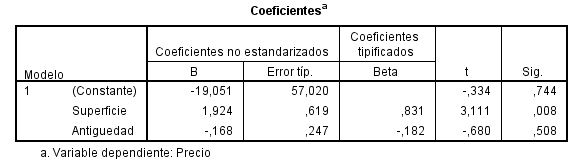
En la tabla de coeficientes figuran los parámetros estimados del modelo de regresión. Por lo tanto, la ecuación de regresión ajustada está dada por:
yˆ = -19.051 + 1.924x1 – 0.168x2
- El precio estimado del piso disminuye en 19051 euros si no se tiene en cuenta la supercie en m2 ni los años de antiguedad.
- Por cada m2 de superficie el precio del piso esperado aumenta en 1924 euros, supuesto que permanece constante los años de antiguedad
- Por cada año de antiguedad el precio del piso esperado disminuye 168 euros, supuesto que permanece constante la superficie del piso en m2.
A la vista de estos resultados parece recomendable que el precio del piso en miles de euros se exprese en función de la supercie del mismo en m2 frente a la otra variable predictiva, años de antiguedad.
2. Contrastar la significación del modelo propuesto.
El contraste de significación del modelo de regresión permite verificar si ninguna variable explicativa es válida para la predicción de la variable de interés.
Este contraste puede escribirse
 El p-valor asociado a este contraste se muestra en la tabla ANOVA:
El p-valor asociado a este contraste se muestra en la tabla ANOVA:
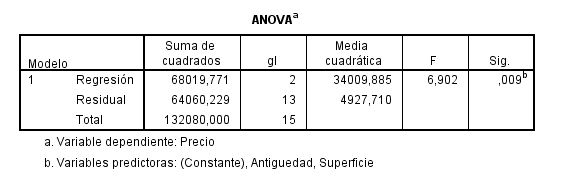
El p-valor asociado al contraste es menor que 0.01, (Sig = 0.009), por lo que rechazamos la hipótesis nula. Esto implica que al menos una de las variables independientes contribuye de forma significativa a la explicación de la variable respuesta.
3. ¿Cuánto será el precio estimado del piso en una conocidad ciudad española para una superficie en 130 m2 y 35 años de antigüedad?
yˆ = -19.051 + 1.924*130 – 0.168*35= 236.949
El precio estimado del piso para una superficie en 130 m2 y 35 años de antigüedad es de 236949 euros
4. ¿Puede eliminarse alguna variable del modelo? Razona la respuesta

Realizamos dos contrastes de hipótesis, uno para cada coeficiente que acompaña a cada variable explicativa ( i = 1, 2)
Para la variable Antigüedad p-valor = 0.508 > α = 0.05, por lo que no rechazamos la hipótesis nula de significación de esta variable. Dicha variable no es válida para predecir el precio de un piso y por tanto puede ser eliminada del modelo.
5. Coeficiente de determinación y de determinación corregido. Interpretación.

El coeficiente de determinación es igual a 0.515 y el coeficiente de determinación corregido es igual a 0,440. En este caso no se aprecian grandes diferencias entre los dos coeficientes. El 51.5% de la variación del precio de un piso se explica por su relación lineal con el modelo propuesto. El valor del coeficiente de determinación no es satisfactorio.