GPCA

GPCA is a sparse variant of PCA where, unlike in other sparse PCA algorithms, the model meta-parameters can be identified from visual inspection of the data. It sequentially solves both problems in the application of PCA to data interpretation. First, a set of groups of correlated variables are found in the data by focusing on the shared variance in a MEDA plot. Then, these groups are used to perform group-wise PCA, so that each loading vector is constrained to have non-zero values in a single group of variables. Following this approach, interpretation is simplified to a large extent, since each Group-wise PC (GPC) can be safely interpreted on an individual basis.

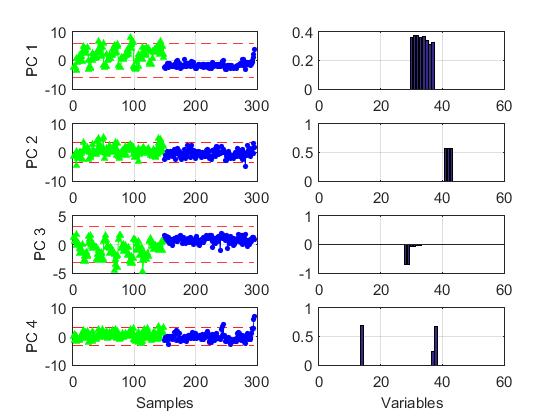
The Figure below shows an example of GPCA over metabolomics data. Scores and loadings for the first four GPCs are given. In the first and in the third components the two clases of observations behave different. The loadings structure is much more simple than in PCA with a large amount of zero loadings. This greatly facilitates interpretation. More details in the reference below.