Mientras que en sus orígenes, las matemáticas sirvieron para algo tan mundano como contar (aritmética), en mi opinión la belleza que han adquirido con el paso de los siglos estriba en su capacidad para expresar la naturaleza: a menudo nos llama la atención la forma de las cosas, sus simetrías, los distintos patrones en su coloración, o cómo evolucionan ciertos fenómenos que dependen del tiempo. Es inherente al ser humano preguntarse sobre qué leyes rigen estos fenómenos, y al intentar entenderlas aparecen de forma natural las matemáticas: para entender un fenómeno de la naturaleza, lo primero que debemos hacer es modelarlo por medio de un objeto matemático, sobre el que podamos aplicar la lógica y deducir propiedades del modelo. Esto a posteriori, nos permitirá concluir propiedades del sistema físico que pretendemos estudiar. Pongamos un ejemplo para ilustrar esto, y que tiene mucho que ver con la asignatura.
Todos tenemos una idea más o menos intuitiva de cuándo una trayectoria se está curvando, o de que una trayectoria se curva más que otra. Pero ¿cómo podríamos justificar una definición rigurosa de curvatura? Veremos la respuesta en clase, pero por ahora quizás sea bueno plantearse algunas preguntas sencillas (analízalas y justifica tus respuestas):
- ¿Qué curvatura debería tener una línea recta? ¿Y una circunferencia?
- ¿Puede variar la curvatura de una trayectoria si nos movemos sobre la misma?
- Si una trayectoria se obtiene a partir de otra aplicando un movimiento rígido, ¿qué relación deberían tener sus curvaturas?
- ¿A qué trayectorias deberíamos asociarles curvatura idénticamente cero? ¿Y qué trayectorias deberían tener curvatura constante no cero?
- Si pensamos en describir una curva en una carretera, podemos hablar de «curva a izquierda» y «curva a la derecha». ¿Cómo podríamos reflejar esto en el concepto de curvatura?
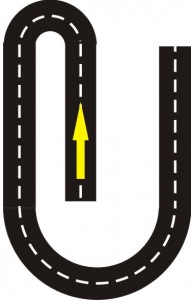
Según lo anterior, podríamos pensar en un primer momento que la curvatura debería medir «el cambio de dirección» de la trayectoria. Y es así, pero es más sutil: Sigamos con el símil anterior de las curvas en una carretera. Imagina dos curvas a izquierda que unen tramos rectos y paralelos de la carretera, pero que una de ellas es más cerrada que la otra:
En cada una de las dos curvas de la figura, el cambio de dirección total es de 180º. Sin embargo, ¿deberían tener estas dos curvas de la carretera la misma curvatura? Claramente, no. De aquí deducimos que la curvatura no sólo debe medir la variación de la dirección en la que se mueve la trayectoria, sino que tiene que tener en cuenta el tiempo que se tarda en cambiar esta dirección.
Hay muchas curvas en el plano y en el espacio de una gran belleza. Describirlas con palabras es demasiado complicado, por lo que los matemáticos han desarrollado un lenguaje para ello. Lo más común es describirlas mediante una parametrización \(\alpha (t)=(x(t),y(t))\) si la curva es plana, o bien \(\alpha (t)=(x(t),y(t),z(t))\) si está en el espacio tridimensional (como la trayectoria de una partícula que se mueve con el tiempo). Aquí entran cuestiones formales como qué coordenadas usar (cartesianas como las anteriores, polares si la curva es plana, cilíndricas o esféricas en el caso de una curva espacial, etc).
Es posible también describir completamente una trayectoria plana (salvo movimientos rígidos) diciendo cómo se curva en cada instante, lo que significa dar una función valuada real que depende del tiempo, la función curvatura \(\kappa =\kappa (t)\). Esta propiedad sigue siendo cierta para curvas en el espacio, pero hay que dar una segunda función «curvatura», que se conoce como la torsión. Esta propiedad de que una curva plana o espacial pueda estar determinada por su función curvatura (y por la torsión si la curva es espacial) puede parecer en principio sorprendente, y de hecho no es cierta en dimensiones superiores, es decir, cuando la trayectoria unidimensional se sustituye por una superficie bidimensional en un ambiente tridimensional.