Meeting of the Network of Nonlocal PDEs and Applications
ICMAT, 20-22 September 2023
This meeting will bring together several researchers from the network “Red de EDPs no locales y aplicaciones” supported by the program “Redes de investigación” of the Ministerio de Ciencia e Innovación. The talks will be focused on the mathematical analysis of PDEs that involve non-local terms.
The conference will take place within the framework of the “2023 Thematic Period on PDEs ICMAT-UAM”.
For full information, please visit the official website of the meeting at https://www.icmat.es/congresos/2023/NLYA/index.php
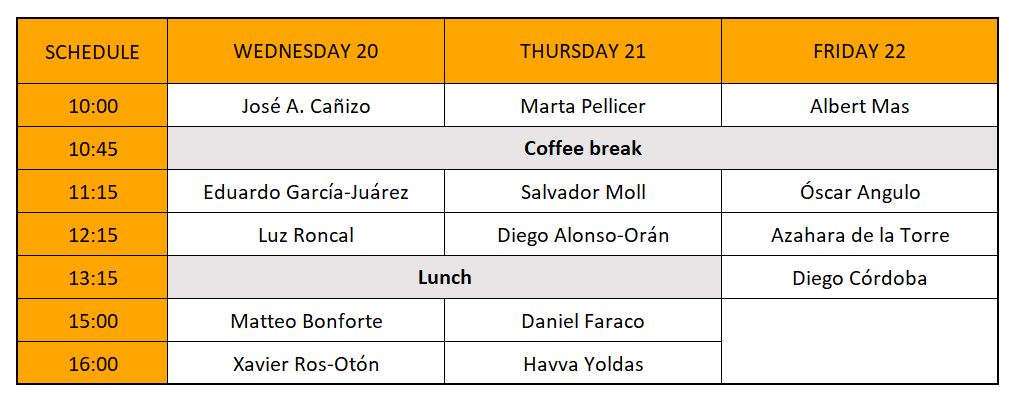
Speakers:
- Diego Alonso Orán (Universidad de la Laguna)
- Óscar Angulo Torga (Universidad de Valladolid)
- Matteo Bonforte (UAM)
- José Alfredo Cañizo (Universidad de Granada)
- Diego Córdoba (ICMAT)
- Azahara de la Torre (Sapienza Università di Roma)
- Daniel Faraco (UAM)
- Eduardo García Juárez (Universidad de Sevilla)
- Albert Mas (UPC)
- Salvador Moll (Universidad de Valencia)
- Marta Pellicer (UdG)
- Luz Roncal (BCAM)
- Xavier Ros-Oton (Universidad de Barcelona)
- Havva Yoldas (Delft Institute of Applied Mathematics)
Program:
Titles and abstracts
- Diego Alonso Orán (Universidad de la Laguna)
- Title: Boundary value problems in magnetohydrodynamics
- Abstract: Magnetohydrodynamics plays a crucial role in understanding the behavior of plasma, electromagnetic fields, and fluid dynamics, providing a fundamental framework for studying phenomena in astrophysics, fusion energy, and space exploration. In this talk, we will present a short survey about the well-posedness of boundary value problems forsteady ideal magnetic fluids. More precisely, we will first focus on the magneto-hydrostatic equations (in two and three dimensions) and conclude with some ongoing work related to the steady magneto-hydrodnamic equations.
- Óscar Angulo Torga (Universidad de Valladolid)
- Title: Numerical integration of an age-structured population model with infinite life span
- Abstract: The choice of the age as a physiological parameter to structure a population and describe its dynamics involves the election of the life-span. An unbounded life-span is useful, not only new models appears in this frame-work, but also it is required by the study of the stability of equilibria. Its numerical integration is usually perform with bounded domains. However, we propose a new numerical method which employs the unbounded domain. It is completely analysed and second order of convergence is established. We report some numerical experiments to show numerically the results and the behaviour of the problem to simulate the evolution of Nicholson’s blowfies model [1].
References
[1] A.J. Nicholson. The self-adjustement of population to change. Cold Spring Harbor Symp. Quant. Biol., 22:153–173, 1957.
- José Alfredo Cañizo (Universidad de Granada)
- Title: Improved asymptotic bounds for the heat equation on exterior domains
- Abstract: We use entropy methods to show that the heat equation with Dirichlet boundary conditions on the complement of a compact set in R^d shows a self-similar behaviour much like the usual heat equation on R^d, once we account for the loss of mass due to the boundary. Giving good lower bounds for the fundamental solution on these sets is surprisingly a relatively recent result, and we find some improvements using some advances in logarithmic Sobolev inequalities. In particular, we are able to give optimal asymptotic bounds for large times for the fundamental solution with an explicit approach rate in dimensions larger than 2, and some new bounds in dimension 2.
This is a work in collaboration with Alejandro Gárriz and Fernando Quirós.
- Azahara de la Torre (Sapienza Università di Roma)
- Title: Qualitative properties of singular solutions to the fractional Yamabe problem
- Abstract: In this talk we will focus on the qualitative properties of the solutions to the fractional Yamabe problem in the n-dimensional Euclidean space which present an isolated singularity. In particular, we will see that the Morse index of any such solution is infinity. The proof uses an Emden Fowler type transformation, so that we can pass to a nonlocal problem posed in the 1-dimensional Euclidean space.
This is a joint work with Sergio Cruz-Blázquez and David Ruiz
- Albert Mas (UPC)
- Title: Periodic surfaces with constant nonlocal mean curvature
- Abstract: In this talk I will present a joint work with Xavier Cabré and Gyula Csató on the existence of periodic surfaces of revolution which have constant nonlocal mean curvature (CNMC). These surfaces may be considered a nonlocal (or fractional) analogue of the classical Delaunay cylinders. Our approach is based on variational methods and yields the existence of CNMC periodic surfaces for every given volume within a slab. In the talk I will also comment their symmetry properties (derived from rearrangement inequalities) as well as related stability results.
- Salvador Moll (Universidad de Valencia)
- Title: Anisotropic inverse mean curvature flow
- Abstract: In this talk, I will present recent results in collaboration with Esther Cabezas-Rivas and Marcos Solera (U. Valencia) concerning the analogous to the inverse mean curvature flow in the presence of an anisotropy (including the case of crystalline anisotropies). I will show the construction of weak solutions of the anisotropic inverse mean curvature flow under very mild assumptions both on the anisotropy and on the initial data. The existence is shown by means of an approximation procedure with anisotropic p-harmonic functions. Our notion of weak solution, which turn out to be unique, still recovers variational and geometric properties similar to those introduced by Huisken-Ilmanen in the classical isotropic setting. We also reach classical results like continuity or exponential growth of the perimeter, as well as outward minimizing properties of the sublevel sets. Moreover, by assuming the extra regularity given by an interior rolling ball condition, the solutions are shown to be continuous and satisfy Harnack inequalities. Finally, I will show some examples of explicit solutions.
- Marta Pellicer (UdG)
- Title: The Moore-Gibson-Thompson equation with heat conduction in $\mathbb{R}^N$: Fourier versus Cattaneo
- Abstract: The MGT equation with heat conduction is considered in $\mathbb{R}^N$. We first consider a Fourier law of heat conduction ([1]) and, second, a Cattaneo law ([2]). In the appropriate functional setting we can see that both thermoviscoelastic models are well-posed, both in the critical and subcritical cases. Then, using the energy method in the Fourier space, we obtain the decay rate of a norm related to the solution for each of the previous models and, therefore, their asymptotic stability. The optimality of the previous results is also discussed, using the eigenvalues expansion method, togehter with the regularity-loss phenomenon. Also, we compare these results between both thermal law cases, and with the Cauchy problem without heat conduction.
[1] M. Pellicer and B. Said-Houari. On the Cauchy problem of the standard linear solid model with Fourier heat conduction, ZAMP (2021).
[2] M. Pellicer and B. Said-Houari. On the Cauchy problem of the standard linear solid model with Cattaneo heat conduction. Asympt. Anal. (2022).
- Luz Roncal (BCAM)
- Title: Discrete and continuous elliptic operators often exhibit different unique continuation properties
- Abstract: Discrete and continuous elliptic operators often exhibit different unique continuation properties: uniqueness features which hold in the continuous setting stop being true in discrete scenarios. In particular, and in contrast with the fractional continuous Laplacian, which enjoys rigidity properties in the form of global unique continuation, we will show that these phenomena fail to hold in general for the fractional discrete Laplacian. We will also discuss quantitative versions of unique continuation which illustrate how the properties in the continuous setting may be recovered if small correction factors are added.
Joint work with Aingeru Fernández-Bertolin and Angkana Ruland.
- Xavier Ros-Oton (Universidad de Barcelona)
- Title: Integro-differential elliptic equations
- Abstract: In this talk we present some new regularity results that are contained in the forthcoming book "Integro-differential elliptic equations" (Birkhäuser, 2024), written jointly with X. Fernández-Real.
More precisely, we first characterize the most general class of Lévy-type operators of order 2s, and then develop the regularity theory for such general class of operators. At the end of the talk, we will list some open problems in this context.
- Havva Yoldas (Delft Institute of Applied Mathematics)
- Title: An existence result for a degenerate cross-diffusion system
- Abstract: We look at a cross-diffusion system consisting of two Fokker-Planck equations where the gradient of the density for each species acts as a potential for the other one. It is a degenerate system in the sense that it loses its parabolic behavior on some part of the domain. However, the system is also the gradient flow for the Wasserstein distance of a functional which is not lower semi continuous. We then compute the convexification of the integrand (thus the lower semi continuous envelope of the functional) and provide an existence result in a suitable sense for the gradient flow of the corresponding relaxed functional. This is a joint work with R. Ducasse (Paris) and F. Santambrogio (Lyon).
Registered Participants:
- Renzo Bruera (Universitat Politècnica de Catalunya)
- Juan Campos (Universidad Granada)
- Arturo de Pablo (Universidad Carlos III de Madrid)
- María del Mar González (Universidad Autónoma de Madrid)
- David Mur Callizo (Universidad Autónoma de Madrid)
- Prashant Kumar Pandey (VIT Bhopal University)
- Marta Pellicer Sabadí (Universitat de Girona)
- Marcos Solera Diana (Universitat de València)
Practical Information:
The main website of the meeting is https://www.icmat.es/congresos/2023/NLYA/index.php.
The deadline for registration is September 15th. In order to register, please visit this page.