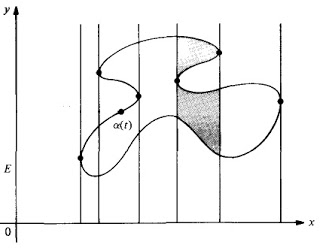
Dentro de las curvas planas tenemos unas especialmente sencillas: son las curvas cerradas simples. Intuitivamente, éstas son las curvas que encierran recintos del plano (con borde de clase \(C^{\infty }\)):
Diremos que una curva \(C^{\infty }\) \(\alpha \colon [a,b]\to \mathbb{R}^2\) es cerrada si \(\alpha ^{(k)}(a)=\alpha ^{(k)}(b)\) para todo \(k\in \mathbb{N}\cup \{ 0\} \). Un resultado topológico, llamado el teorema de la curva de Jordan, asegura que toda curva cerrada simple plana divide a \(\mathbb{R}^2\) en dos recintos, uno acotado (el dominio interior, al que denotaremos por \(\Omega \)) y su complementario, que es no acotado. Tenemos entonces dos cantidades ligadas a \(\alpha \): su longitud \({\displaystyle L=\int _a^b\| \alpha'(t)\| \, dt}\), y el área \(A(\Omega )\) del dominio interior encerrado por \(\alpha \).
Dedicaremos esta entrada a descubrir una fórmula explícita para calcular esta área, y dejaremos la relación básica entre área y longitud (o perímetro) para una entrada posterior. Si escribimos \(\alpha (t)=(x(t),y(t))\) y orientamos \(\alpha \) de forma que el dominio interior \(\Omega \) siempre quede a la izquierda de la curva, entonces el área de \(\Omega \) se calcula así:
$$
A(\Omega )\stackrel{(a)}{=}-\int _a^by(t)x'(t)\, dt\stackrel{(b)}{=}\int _a^bx(t)y'(t)\, dt
\stackrel{(c)}{=}\frac{1}{2}\int _a^b(xy’-yx’)\, dt.
$$
De hecho, la fórmula anterior es válida aunque \(\alpha \) no sea de clase \(C^{\infty }\): basta que sea \(C^1\) a trozos.
A continuación veremos porqué la fórmula anterior es cierta. De momento, dejamos (a) para más tarde.
- Usa la regla de Barrow para probar que la igualdad en (b) es cierta.
- Deduce (c) de la igualdad en (b).
- Prueba (a) en el siguiente caso particular: El recinto \(\Omega \) está delimitado por dos segmentos verticales y dos grafos de funciones \(f,h\colon [x_0,x_1]\to \mathbb{R}\) con \(f\lt h\), como en la siguiente figura:
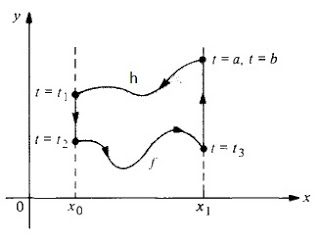
En la figura anterior, hemos marcado los cuatro vértices del recinto de forma que uno es \(\alpha (a)=\alpha (b)\), luego \(\alpha \) recorre el grafo de \(h\) de derecha a a izquierda hasta llegar a \(\alpha (t_1)\); entre \(\alpha (t_1)\) y \(\alpha(t_2)\) recorremos un segmento vertical en dirección descendente, para luego recorrer el grafo de \(f\) de izquierda a derecha, y terminar con un segmento vertical ascendente desde \(\alpha (t_3)\) hasta \(\alpha (b)\).
Para probar el caso general de la fórmula (a), supondremos que existe una dirección en \(\mathbb{R}^2\); de forma que la curva \(\alpha \) sólo es tangente a esa dirección un número finito un número finito de veces, como en la siguiente figura:
Admitiendo lo anterior, prueba la igualdad (a).
Hay una forma más directa de demostrar la fórmula de \(A(\Omega )\), pero necesita la llamada fórmula de Green (o el teorema de la divergencia, o el teorema de Stokes). La fórmula de Green nos dice que si \(p(x,y),q(x,y)\) son funciones de clase \(C^1\) definidas en un abierto que contiene a \(\Omega \), entonces
$$
\int _{\Omega }\left(\frac{\partial q}{\partial x}-\frac{\partial p}{\partial y} \right) dxdy=\int _a^b\left[ p(x(t),y(t))x'(t)+q(x(t),y(t))y'(t)\right] dt.
$$
Prueba la fórmula \({\displaystyle 2A(\Omega )=\int _a^b(xy’-yx’)\, dt}\) usando la fórmula de Green.
La fórmula de Green es una consecuencia directa del Teorema de Stokes, que quizás veáis en la asignatura Variedades Diferenciables de 4º curso, aunque es muy posible que ya os haya aparecido en otra asignatura.