Olimpiadas de Matemáticas
Página de preparación y problemas

Elige un tema
| Aritmética |
| Geometría |
| Polinomios |
| Desigualdades |
| Álgebra |
| Combinatoria |
| Invariantes |
Lección 1. Operaciones con polinomios
Es frecuente encontrar problemas de competición que tratan con polinomios y sus propiedades. Este tema permite plantear cuestiones fáciles pero también otras muy complejas, debido a la estructura algebraica tan rica que esconden estas expresiones en apariencia sencillas. En la enseñanza preuniversitaria, el estudio de polinomios se reduce prácticamente a la resolución de ecuaciones polinómicas o al estudio de funciones polinómicas. Sin embargo, las olimpiadas recurren a otros aspectos de los polinomios como la divisibilidad o propiedades aritméticas de polinomios de coeficientes enteros. En estas lecciones profundizaremos en estos temas con el objeto de poder resolver los problemas de mayor dificultad.
Los números $a_0,a_1,\ldots,a_n$ se llaman coeficientes del polinomio. Suele usarse la notación $\mathbb{Z}[x]$, $\mathbb{Q}[x]$, $\mathbb{R}[x]$ y $\mathbb{C}[x]$ para hacer referencia al conjunto de todos los polinomios con coeficientes enteros, racionales, reales o complejos, respectivamente. Un polinomio especial es el polinomio nulo $P(x)=0$ en que todos los coeficientes son cero. Dado un polinomio no nulo, a la mayor potencia de $x$ cuyo coeficiente no es nulo se le llama grado del polinomio. Consideremos los siguientes ejemplos: \begin{eqnarray*} P(x)&=&-4\\ Q(x)&=&-2x^2-\tfrac{2}{3}x+1\\ R(x)&=&x^3-\pi\\ S(x)&=&x^4+4x^3+6x^2+4x+1 \end{eqnarray*} El polinomio $P(x)$ es un polinomio de grado $0$ (también se dice que es constante ya que no depende de la variable o indeterminada). El polinomio $Q(x)$ tiene grado $2$ y coeficientes racionales, el polinomio $R(x)$ es de grado $3$ y tiene coeficientes reales pero no racionales (ya que el número $\pi$ no es racional) y el polinomio $S(x)$ tiene grado $4$ y coeficientes enteros (que también son racionales, reales o complejos). No obstante, la indeterminada $x$ no es un número de ningún tipo, sólo un símbolo que nos permitirá hacer distintas operaciones.
Podemos estar tentados de llamar polinomios a otras expresiones parecidas a las de la definición, como pueden ser $x^2+2x^{-2}-5$ o $x^{3,5}+3x^3-2x^2+1$, pero no lo son. Los exponentes de $x$ tienen que ser números naturales.
Suma y producto de polinomios
Los polinomios se pueden sumar y multiplicar usando las reglas usuales de la suma y producto de números y tratando a la $x$ como una incógnita. Por ejemplo, podemos usar la propiedad distributiva para calcular $3x^2-5x^2=(3-5)x^2=-2x^2$ o bien sumar exponentes de $x$ para calcular $(3x^2)(-5x^2)=-15x^4$. De esta forma, si escribimos \begin{eqnarray*} P(x)&=&a_0+a_1x+a_2x^2+\ldots+a_n x^n,\\ Q(x)&=&b_0+b_1x+b_2x^2+\ldots+b_m x^m, \end{eqnarray*} la suma $P(x)+Q(x)$ es otro polinomio que se calcula de forma muy sencilla: \begin{eqnarray*}P(x)+Q(x)&=&(a_0+b_0)+(a_1+b_1)x+\ldots+(a_n+b_n)x^n\\ &&+b_{n+1}x^{n+1}+\ldots+b_mx^m, \end{eqnarray*} donde hemos supuesto que $m\geq n$. En otras palabras, para sumar dos polinomios, sólo hay que sumar los coeficientes de los monomios del mismo grado. En cuanto al producto, tenemos que usar la propiedad distributiva para llegar a que \begin{eqnarray*} P(x)Q(x)&=&a_0b_0+a_1b_0x+a_2b_0x^2+\ldots+a_nb_0 x^n\\ &&+a_0b_1x+a_1b_1x^2+a_2b_1x^3+\ldots+a_nb_1x^{n+1}\\ &&\quad\vdots\\ &&+a_0b_mx^m+a_1b_mx^{m+1}+a_2b_mx^{m+2}+\ldots+a_nb_mx^{m+n}. \end{eqnarray*} Ahora sólo hay que agrupar los términos del mismo grado para obtener un polinomio escrito en la forma de la definición. Puede ser un proceso un poco laborioso si los polinomios tienen muchos términos pero no deja de ser muy intuitivo. Un caso particular interesante de producto es cuando multiplicamos un polinomio $P(x)$ por un polinomio constante $Q(x)=a$, lo que equivale a multiplicar por dicha constante, es decir, \[kP(x)=ka_0+ka_1x+ka_2x^2+\ldots+ka_nx^n.\] Es muy fácil comprobar que se cumplen las siguientes propiedades:
- El grado de la suma de dos polinomios es el máximo de sus grados.
- El grado del producto de dos polinomios es la suma de sus grados.
La suma y el producto de polinomios se comportan de forma muy parecida a la suma y producto de números. De hecho, se cumplen las siguientes propiedades para cualesquiera polinomios:
- $P(x)+Q(x)=Q(x)+P(x)$,
- $P(x)Q(x)=Q(x)P(x)$,
- $P(x)+(Q(x)+R(x))=(P(x)+Q(x))+R(x)$,
- $P(x)(Q(x)R(x))=(P(x)Q(x))R(x)$,
- $P(x)(Q(x)+R(x))=P(x)Q(x)+P(x)R(x),$
- $P(x)+0=P(x)$,
- $1\cdot P(x)=P(x)$.
Todo esto se puede escribir formalmente como sigue (se deja como ejercicio ver a cuál de las anteriores fórmulas corresponde cada propiedad enunciada):
- La suma de polinomios es asociativa, conmutativa y tiene por elemento neutro al polinomio nulo $0$.
- El producto de polinomios es asociativo, conmutativo y tiene por elemento neutro al polinomio constante 1.
- El producto de polinomios es distributivo respecto de la suma.
También se puede hablar de la potencia de un polinomio $P(x)^n$, que no es más que multiplicarlo por sí mismo $n$ veces, resultando otro polinomio.
Evaluación de polinomios
La notación $P(x)$ para un polinomio sugiere que un polinomio es una función que a cada valor de $x$ le asigna un valor $P(x)$ que se calcula mediante la fórmula que define al polinomio. De hecho, dado un número complejo $b$, podemos evaluar un polinomio $P(x)=a_0+a_1x+\ldots+a_nx^n$ sustituyendo cada aparición de $x$ por $b$, es decir, \[P(b)=a_0+a_1b+\ldots+a_nb^n.\] Algunas evaluaciones concretas nos pueden dar información relevante. Por ejemplo, si tomamos $b=0$ o $b=\pm 1$, tenemos que \begin{eqnarray*} P(0)&=&a_0\quad \text{(es el término independiente)}\\ P(1)&=&a_0+a_1+\ldots+a_n\quad \text{(es la suma de los coeficientes)}\\ P(-1)&=&a_0-a_1+\ldots+(-1)^na_n\quad \text{(es la suma alternada de los coeficientes)}\\ \end{eqnarray*}
Un caso particular de evaluación es la composición de dos polinomios $P(Q(x))$. Por ejemplo, si $P(x)=x^2+1$ y $Q(x)=3x-2$, entonces podemos escribir \begin{eqnarray*} P(Q(x))&=&P(3x-2)=(3x-2)^2+1=9x^2-12x+5,\\ Q(P(x))&=&Q(x^2+1)=3(x^2+1)-2=3x^2+1. \end{eqnarray*}
Rectas y parábolas
Si seguimos pensando en un polinomio con coeficientes reales como una función, como tal podemos obtener una representación gráfica suya. En ocasiones, conocer dicha gráfica (o alguna información relevante de ella) aporta cierta intuición para resolver un problema. En esta lección introductoria vamos a recordar cómo se representan los polinomios de grado menor o igual que $2$ y más adelante daremos algunas ideas para grados superiores.
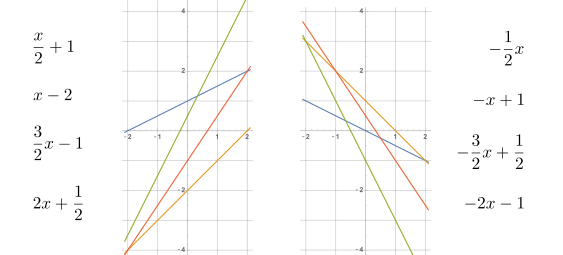
Todo polinomio de grado menor o igual que $1$ es de la forma $P(x)=ax+b$ para ciertos $a,b\in\mathbb{R}$. Por tanto, su gráfica será la curva del plano dada por la ecuación $y=ax+b$, que es una recta de pendiente $a$ y que pasa por el punto $(0,b)$. Esto quiere decir que $y$ avanza $a$ unidades cuando $x$ aumenta una unidad, lo que permite representar fácilmente la gráfica del polinomio. En la siguiente imagen pueden verse 8 polinomios de grado $1$, los cuatro de la derecha con pendiente negativa y los de la izquierda con pendiente positiva. Se deja como ejercicio decir a cuáles de las fórmulas propuestas corresponde cada gráfica. ¿Cómo es la gráfica de un polinomio de grado cero?
Pensemos ahora en un polinomio de grado $2$ cuya gráfica se corresponda con la curva $y=ax^2+bx+c$, siendo $a\neq 0$ (¡para que el grado sea $2$!). Esta curva se llama parábola y tiene propiedades geométricas muy interesantes. Hay muchas maneras de representar una parábola, aunque aquí lo haremos completando cuadrados, es decir, expresando \[y=ax^2+bx+c=a\left(x+\frac{b}{2a}\right)^2+c-\frac{b^2}{4a}.\] Esto nos dice que si tomamos $y_0=y-(c-\frac{b^2}{4a})$ y $x_0=x+\frac{b}{2a}$, entonces podemos expresar la parábola como $y_0=ax_0^2$. Esta parábola es fácil de representar ya que pasa por el $(0,0)$ y por $(\pm 1,a)$. Ahora sólo hay que deshacer el cambio de variable y trasladar el punto $(0,0)$ al vértice real de la parábola, que es el punto de coordenadas $(\frac{-b}{2a},c-\frac{b^2}{4a})$. Dicho de otro modo, las gráficas de dos parábolas que tienen el mismo valor de $a$ son la misma salvo una traslación.
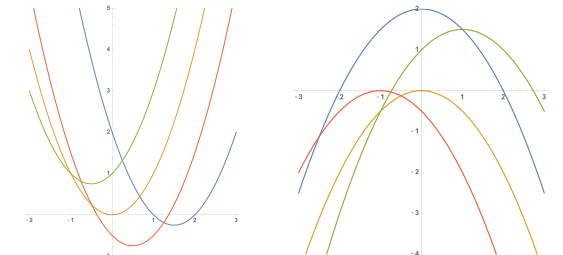
En la siguiente imagen se muestran parábolas con $a=1$ a la izquierda y parábolas con $a=\frac{-1}{2}$ a la derecha. ¿Sabrías encontrar las expresiones de los correspondientes polinomios sabiendo que tienen coeficientes enteros o de la forma $\frac{m}{2}$ siendo $m$ entero?
El siguiente ejercicio da una forma sencilla para saber cuándo una función polinómica es par o impar. Recordemos que una función $f(x)$ es par si $f(x)=f(-x)$ (es decir, si su gráfica es simétrica respecto del eje de ordenadas) y es impar cuando $f(-x)=-f(x)$ (es decir, si su gráfica es simétrica respecto del origen de coordenadas).
- Demostrar que un polinomio $P(x)$ es una función par si y sólo si no tiene monomios de grado impar.
- Demostrar que un polinomio $P(x)$ es una función impar si y sólo si no tiene monomios de grado par.
Informar de error en enunciado Informar de procedencia del problema
Hemos probado ya el enunciado para $(a,b)=(0,0)$. Para un $(a,b)$ cualquiera, la gráfica de $P$ es simétrica respecto de $(a,b)$ si, y sólo si, la gráfica de $R(x)=P(x+a)-b$ es simétrica respecto del origen (hemos hecho una traslación del punto $(a,b)$ al origen). Por lo que hemos probado antes, esto ocurre si, y sólo si, $R(x)=xQ(x)$ para cierto polinomio $Q(x)$. Deshaciendo el cambio, la gráfica de $P$ es simétrica respecto de $(a,b)$ si, y sólo si, $P(x)=R(x-a)+b=(x-a)Q\bigl((x-a)^2\bigr)+b$ para cierto polinomio $Q(x)$.
Nota. Este es un ejercicio muy mecánico. Las ideas fundamentales que se desprenden de la solución y que hay que aprender son: (1) que la gráfica de una función es simétrica respecto del origen si, y sólo si, es una función impar; y (2) que la gráfica de $f(x+a)-b$ es la misma que la gráfica de $f(x)$ después de aplicarle una traslación que lleva $(a,b)$ al $(0,0)$.
Informar de error en enunciado Informar de procedencia del problema
- Si \(P(0)=1\), entonces vamos a probar que el polinomio es constante uno. Por reducción al absurdo, si así no fuera, podemos escribir \(P(x)=1+a_kx^k+a_{k+1}x^{k+1}+\ldots+a_nx^n\) para \(k\geq 1\) y \(a_k\neq 0\) (es decir, \(k\) es el grado del primer monomio no nulo aparte del término independiente). Entonces, el término de grado \(k\) en \(P(x^2)\) es cero mientras que en \(P(x)^2\) es \(2a_kx^k\), luego tiene que ser \(a_k=0\), lo cual es una contradicción.
- Si \(P(0)=0\), entonces existen \(k\in\mathbb{N}\) y un polinomio \(Q(x)\) tal que \(P(x)=x^kQ(x)\) y \(Q(0)\neq 0\). La condición \(P(x^2)=P(x)^2\) se escribe ahora como \(x^{2k}Q(x^2)=x^{2k}Q(x)^2\) y \(Q\) también cumple el enunciado con \(Q(0)\neq 0\). Por el apartado (a), tiene que ser \(Q(x)=1\), luego \(P(x)=x^k\).
Informar de error en enunciado Informar de procedencia del problema