Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Todos los problemas
IV Olimpiada Iberoamericana de Matemáticas — 1989
Sesión 1 — La Habana (Cuba), 10 de abril de 1989
En efecto, si $y\gt -1$, en la primera ecuación tendríamos que $x\gt z$ y en la tercera que $x\lt z$, lo que nos lleva a una contradicción. Si ocurriera que $y\lt -1$, tendríamos que de la primera ecuación $x-z=-1-y\gt 0$ y, de la tercera, que $-x^3+z^3=-1-y^3\gt 0$, luego volvemos a caer en la misma contradicción. Deducimos entonces que $y=-1$.
Sustituyendo $y=-1$, tenemos que $x=z$ en la primera ecuación y $x^2+z^2=2$ en la segunda, luego $x=z=\pm 1$, de donde obtenemos las soluciones propuestas anteriormente. Observemos que ambas cumplen la tercera ecuación luego son las únicas soluciones.
Informar de error en enunciado Informar de procedencia del problema
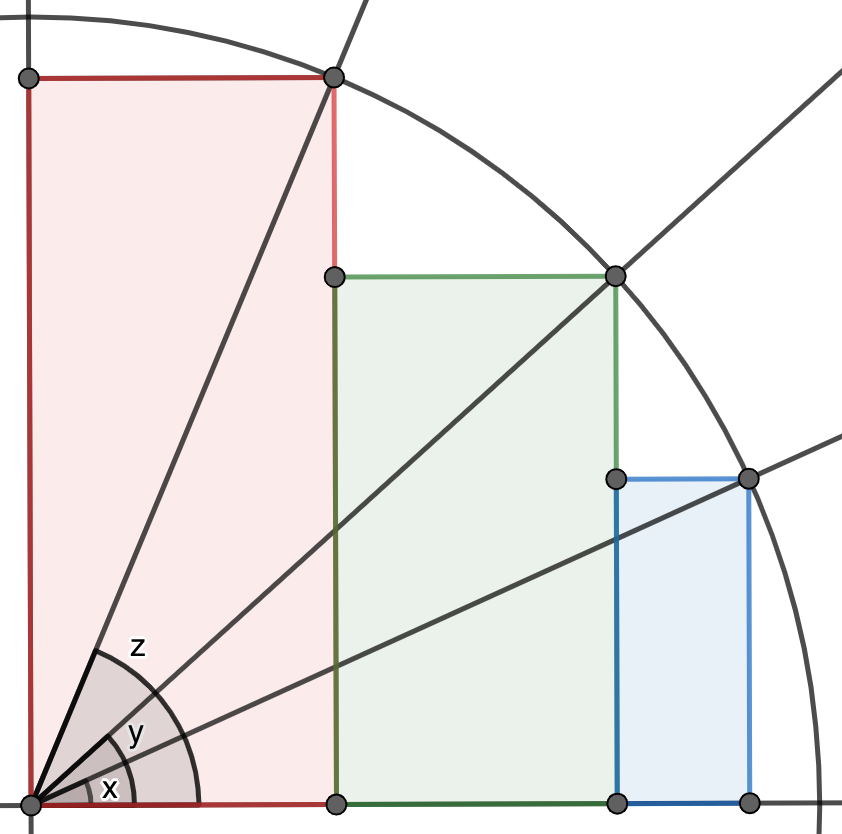
Informar de error en enunciado Informar de procedencia del problema
Nota. La cota $\frac{1}{16}$ parece no ser óptima.
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — La Habana (Cuba), 11 de abril de 1989
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Una forma de obtener soluciones de la ecuación de Pell es la siguiente (ver la nota). Partimos de una solución concreta no trivial, por ejemplo, tomaremos $p_1=5$, $q_1=2$ (esta solución se encuentra tras probar un poco). Se tiene entonces una sucesión de soluciones $(p_n,q_n)$ tomando $p_n$ y $q_n$ como los únicos números naturales que verifican $(5+2\sqrt{6})^n=p_n+q_n\sqrt{6}$. Podemos desarrollar \[p_n+q_n\sqrt{6}=(5+2\sqrt{6})(p_{n-1}+q_{n-1}\sqrt{6})=(5p_{n-1}+12q_{n-1})+(2p_{n-1}+5q_{n-1})\sqrt{6},\]
lo que nos da la recurrencia \[\left\{\begin{array}{l}p_n=5p_{n-1}+12q_{n-1},\\q_n=2p_{n-1}+5q_{n-1}.\end{array}\right.\] También tenemos así una recurrencia para $r_n=\frac{p_n}{q_n}$ haciendo lo siguiente: \[r_n=\frac{p_n}{q_n}=\frac{5p_{n-1}+12q_{n-1}}{2p_{n-1}+5q_{n-1}}=\frac{5\frac{p_{n-1}}{q_{n-1}}+12}{2\frac{p_{n-1}}{q_{n-1}}+5}=\frac{5r_{n-1}+12}{2r_{n-1}+5}.\] La función $f(x)=\frac{5x+12}{2x+5}$ cumple que $f(x)=x$ si y solo si $x=\pm\sqrt{6}$. Teniendo en cuenta que $\lim_{x\to\infty}f(x)=\frac{5}{2}\gt \sqrt{6}$, es fácil ver que \[\sqrt{6}\lt x\lt f(x)\lt\frac{5}{2}\quad \text{para todo } x\gt\sqrt{6}.\] De esta manera, teniendo en cuenta que $r_1=\frac{p_1}{q_1}=\frac{5}{2}$, se sigue que $\sqrt{6}\lt r_{n-1}\lt r_n\leq\frac{5}{2}$ para todo $n\in\mathbb{N}$. Esto tiene dos consecuencias que resuelven el problema.- En primer lugar, todos los $r_n$ son distintos, lo que nos dice que hay un número infinito de soluciones distintas al problema original. Esto es consecuencia de que $x$ e $y$ son funciones racionales de $r$ y una función racional no puede tomar el mismo valor para infinitos valores de la variable si no es idénticamente nula.
- En segundo y último lugar, las expresiones $\frac{r^2-r-3}{r^2-6}$ y $\frac{r-2}{r^2-6}$ son positivas para todo $r\gt \sqrt{6}$ luego todas nuestras soluciones $r_n$ hacen a $x$ e $y$ positivos.
Nota. Lo que hemos usado es que la ecuación de Pell $p^2-6q^2=1$ puede verse como números $p+q\sqrt{6}$ de norma $1$ en el anillo $\mathbb{Z}[\sqrt{6}]$. La norma de $a+b\sqrt{6}\in\mathbb{Z}[\sqrt{6}]$, con $a,b\in\mathbb{Z}$, se define de hecho como \[N(a+b\sqrt{6})=a^2-6b^2=(a+b\sqrt{6})\cdot(a-b\sqrt{6}).\] En realidad, se define como el valor absoluto de lo anterior, pero esto no es relevante para lo que vamos a decir porque lo interesante es que $N$ es multiplicativa, es decir, \[N((a+b\sqrt{6})(c+d\sqrt{6}))=N(a+b\sqrt{6})N(c+d\sqrt{6}).\] Desarrollando esta ecuación, simplemente estamos diciendo que lo siguiente se cumple para cualesquiera $a,b,c,d\in\mathbb{Z}$: \[(ac+6bd)^2-6(ad+bc)^2=(a^2-6b^2)(c^2-6d^2).\] Por lo tanto, si encontramos un número $a+b\sqrt{6}$ de norma $1$, todas sus potencias de exponente natural también tendrán norma $1$. Esto es lo que se ha usado en el problema.
Informar de error en enunciado Informar de procedencia del problema