Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Usando el teorema de Pitágoras y teniendo en cuenta el origen $O=(0,0)$, las longitudes de los lados al cuadrado son \[OA^2=a^2+11^2,\qquad OB^2=b^2+37^2,\qquad AB^2=(a-b)^2+26^2.\] Por tanto, podemos resumir la condición de ser equilátero en un sistema de dos ecuaciones con las dos incógnitas $a$ y $b$: \begin{align*} OA=OB&\ \Longleftrightarrow\ a^2-b^2=1248\\ OA=AB&\ \Longleftrightarrow\ 2ab-b^2=555. \end{align*} Como cambiar ambas incógnitas de signo sigue produciendo una solución y no cambia el producto $ab$, podemos suponer que $a$ es positivo y despejar de la primera ecuación $a=\sqrt{1248+b^2}$. Sustituyendo esto en la segunda, obtenemos que \begin{align*} 2b\sqrt{1248+b^2}-b^2=555&\ \Longleftrightarrow\ 4b^2(1248+b^2)=(555+b^2)^2\\ &\ \Longleftrightarrow\ 3(b^4+3882 b^2-308025=0\\ &\ \Longleftrightarrow\ b^4+1294 b^2-102675=0. \end{align*} Esta ecuación se puede resolver como una bicuadrada, lo que nos da $b^2=75$ o bien $b^2=-1379$. Esta segunda solución hemos de descartarla ya que $b$ es un número real. Por tanto, de la ecuación original $2ab-b^2=555$, deducimos finalmente que \[ab=\tfrac{1}{2}(555+b^2)=\tfrac{1}{2}(555+75)=315.\]

Nota. No es difícil terminar el razonamiento y ver que las soluciones al problema son \[(a,b)=\left(21\sqrt{3},5\sqrt{3}\right)\qquad\text{y}\qquad (a,b)=\left(-21\sqrt{3},-5\sqrt{3}\right).\]

Solución. Consideremos un punto $P=(a,b)$ en general con sus dos coordenadas enteras no negativas, es decir, $a,b\in\mathbb{N}$. Vamos a demostrar previamente que el segmento $OP$ contiene otro punto de coordenadas enteras si, y sólo si, $a$ y $b$ no son primos relativos.

Por un lado, si existe tal punto en $OP$, esto quiere decir que existen $c,d\in\mathbb{N}$ y $0\lt\lambda\lt 1$ tales que $(c,d)=\lambda(a,b)$. En particular, $\lambda=\frac{c}{a}=\frac{d}{b}$ es un número racional. Supongamos que $\lambda=\frac{m}{n}$ como fracción irreducible, luego \[c=\frac{m}{n}a,\qquad d=\frac{m}{n}b,\] de forma que $n$ debe ser un divisor común a $a$ y $b$. Observemos que $n\gt 1$ ya que $0\lt \lambda\lt 1$, luego hemos probado que $a$ y $b$ no son primos entre sí. Recíprocamente, si $n\gt 1$ es un divisor común a $a$ y $b$, entonces el punto $(c,d)=(\frac{a}{n},\frac{b}{n})$ es un punto de coordenadas enteras en el segmento $OP$, lo que concluye la demostración.

Con esta información, el problema se traduce en ver cuántos números enteros $k$ entre $1$ y $1998$ son primos relativos con $1000$. Como $1000=2^3\cdot 5^3$, estamos buscando los valores de $k$ que no tienen factores primos $2$ ni $5$. De los $1998$ números considerados, hay $999$ múltiplos de $2$, $399$ múltiplos de $5$ y $199$ múltiplos de $10$ (¿sabrías contarlos rápidamente?). Por tanto, la cantidad de primos relativos con $1000$ (la solución al problema) es: \[1998-999-399+199=799\] (hay que añadir $199$ ya que estamos quitando los múltiplos de $10$ dos veces).

Solución. Consideramos la ecuación \[(\star)\quad \frac{2x-7}{2x^2-2x-5}=k\ \Longleftrightarrow\ 2kx^2-2(k+1)x-5k+7=0.\] El discriminante de esta ecuación de segundo grado es \[\Delta=4(k+1)^2-8k(7-5k)=4(1-12k+11k^2)=44(k-1)(k-\tfrac{1}{11})\] y tiene que ser $\Delta\geq 0$ para que $(\star)$ tenga solución. Deducimos directamente que $(\star)$ tiene solución si y sólo si, $k\geq 1$ o $k\leq \frac{1}{11}$, luego la solución a la cuestión del enunciado es $k=\frac{1}{11}$.

Nota. Esta es una solución sin derivadas, aunque es obvio que el problema se puede resolver fácilmente estudiando máximos y mínimos. Tenemos que \[f(x)=\frac{2x-7}{2x^2-2x-5}\ \Longrightarrow\ f'(x)=\frac{-4(x-1)(x-6)}{(2 x^2-2x-5)^2}\] luego $f'(x)=0$ sólo si $x=1$ o $x=6$. Analizando las asíntotas verticales y horizontales de $f(x)$, se puede ver que no hay valores de $f(x)$ entre el máximo local $f(6)=\frac{1}{11}$ y el mínimo local $f(1)=1$.

Solución.

1. La función $f$ tiene que ser biyectiva ya que $f^{-1}=f$ ($f$ es su propia inversa), lo que nos dice que $f$ permuta los valores del conjunto $A$. Además, como $f(f(x))=x$, la función actúa sobre parejas de elementos de $A$ intercambiando sus valores o bien dejando elementos de $A$ fijos. Habrá tantas funciones $f$ como formas extraer parejas disjuntas de $A=\{1,2,3,4,5,6\}$:
   • Con cero parejas hay una forma de hacerlo (dejar todo fijo).
   • Con una pareja hay $\binom{6}{2}=15$ formas de hacerlo.
   • Con dos parejas hay $\frac{1}{2}\binom{6}{2}\binom{4}{2}=\frac{1}{2}\cdot 15\cdot 6=45$ formas de hacerlo. El razonamiento para obtener esta fórmula es que hay $\binom{6}{2}$ formas de elegir la primera pareja y $\binom{4}{2}$ formas para la segunda (quedan sólo 4 elementos para elegir), pero estamos contando cada configuración dos veces.
   • Con tres parejas hay $\frac{1}{6}\binom{6}{2}\binom{4}{2}\binom{2}{2}=\frac{1}{6}\cdot 15\cdot 6\cdot 1=15$ formas de hacerlo. El razonamiento es similar al anterior, pero estamos contado cada configuración $3!=6$ veces.
   Tenemos así un total de $1+15+45+15=76$ funciones que cumplen este apartado.
2. El razonamiento para este apartado es similar. Observamos que $f$ también es biyectiva ya que cumple $f^{-1}=f\circ f$. Ahora bien, al cumplirse que $f(f(f(x)))=x$ para todo $x\in A$, se sigue que $f$ permuta cíclicamente tríos de elementos de $A$ y deja otros fijos. Ahora bien, cada trío $\{x,y,z\}$ tiene dos posibles permutaciones cíclicas según el orden en que se roten los elementos, que son $x\mapsto y\mapsto z\mapsto x$ y $x\mapsto z\mapsto y\mapsto x$. Tenemos tres casos:
   • Con cero tríos hay una forma de hacerlo (dejar todo fijo).
   • Con un trío hay $\binom{6}{3}=20$ formas de elegir el trío, lo que nos da 20\cdot 2=40$ posibles permutaciones.
   • Con dos tríos hay $\frac{1}{2}\binom{6}{3}\binom{3}{3}=10$ formas de elegir los dos tríos, lo que nos da $10\cdot 4=40$ posibles permutaciones (hay que elegir el orden de rotación en cada trío).
   Tenemos así un total de $1+40+40=81$ funciones que cumplen este apartado.

Solución. Utilizaremos la propiedad de que $x-y$ divide a $p(x)-p(y)$ para cualesquiera números enteros $x$ e $y$ por tener $p(x)$ coeficientes enteros. Razonaremos que no puede existir el entero $k$ por reducción al absurdo suponiendo que sí que existe.

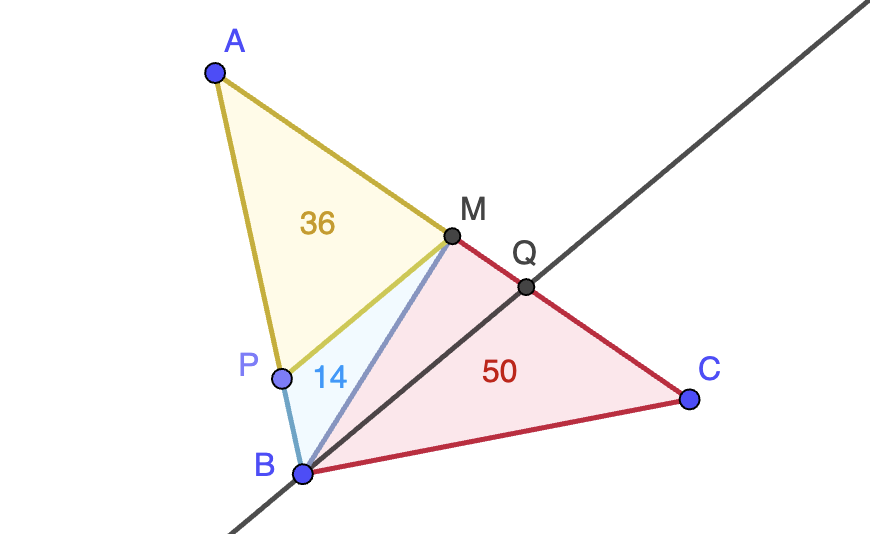
Tomando $x=k$ e $y=a$, esta propiedad nos dice que $k-a$ divide a $p(k)-p(a)=7$, luego $k-a$ tiene que ser igual a $\pm 1$ o $\pm 7$, los factores enteros de $7$. Análogamente, para $x=k$ e $y=a+1$, se tiene que $k-a-1$ divide a $p(k)-p(a+1)=7$, luego $k-a-1$ tiene que ser igual a $\pm 1$ o $\pm 7$, esto es, $k-a$ tiene que ser igual a $-6$, $0$, $2$ u $8$, lo cual es absurdo (tenía que ser $\pm 1$ o $\pm 7$).

Nota. No se ha usado la hipótesis de que $p(a+2)=1$.

Solución. El triángulo $ABC$ se puede descomponer en los triángulos $AMP$, $BPM$ y $MBC$. Sabemos que el área de $AMP$ es $36$ y la de $MBC$ es $50$ (por ser $M$ el punto medio de $AC$); como el área total es 100, deducimos que $BPM$ tiene área $100-50-36=14$. Finalmente, hay que darse cuenta de que $BPM$ y $MPQ$ tienen el mismo área ya que $BQ$ es paralela a $MP$. Por tanto, la respuesta es $14$.

Solución. Observemos que $f^n(x)$ es un polinomio con coeficientes enteros y vamos a probar que su término independiente es $1$. Esto se prueba fácilmente por inducción sobre $n$, teniendo en cuenta que el término independiente se obtiene evaluando en $x=0$. Para $n=1$, tenemos que $f^1(0)=f(0)=1$; supuesto cierto que $f^n(0)=1$ para cierto $n\geq1$, podemos calcular $f^{n+1}(0)=f(f^n(0))=f(1)=1$.

Esto nos dice que, para cada $n\in\mathbb{N}$ podemos expresar $f^{n-1}(x)=x p_{n-1}(x)+1$ para cierto polinomio $g_{n-1}(x)$. Tenemos así que \begin{align*} \mathrm{mcd}(f(x),f^n(x))&=\mathrm{mcd}(f(x),f^{n-1}(f(x)))\\ &=\mathrm{mcd}(f(x),f(x) p_{n-1}(f(x))+1)=1. \end{align*}

Nota. El resultado es también cierto cambiando $f(x)=x^{1997}-x+1$ por cualquier polinomio $f(x)$ con coeficientes enteros y $f(0)=f(1)=1$. También es cierto que $f^n(y)$ y $f^m(y)$ son primos relativos para cualesquier $m,n\in\mathbb{N}$ (basta aplicar el enunciado a $x=f^{m-1}(y)$ con $n+1$ en lugar de $n$).

Solución. En el caso del octógono, tras algunos intentos es muy fácil llegar a una solución, por ejemplo la que se muestra en la imagen más abajo.

En el caso del dodecágono, para demostrar que no se puede, vamos a razonar por reducción al absurdo suponiendo que existen 6 segmentos de distinta longitud que emparejan los 12 vértices. Si numeramos los vértices consecutivamente con números del 1 al 12, habrá siempre 3 de los segmentos que unan un vértice par con uno impar mientras que los otros tres unirán par con par o bien impar con impar. Como entre 1 y 12 hay el mismo número de pares que de impares, hemos llegado a la contradicción buscada.

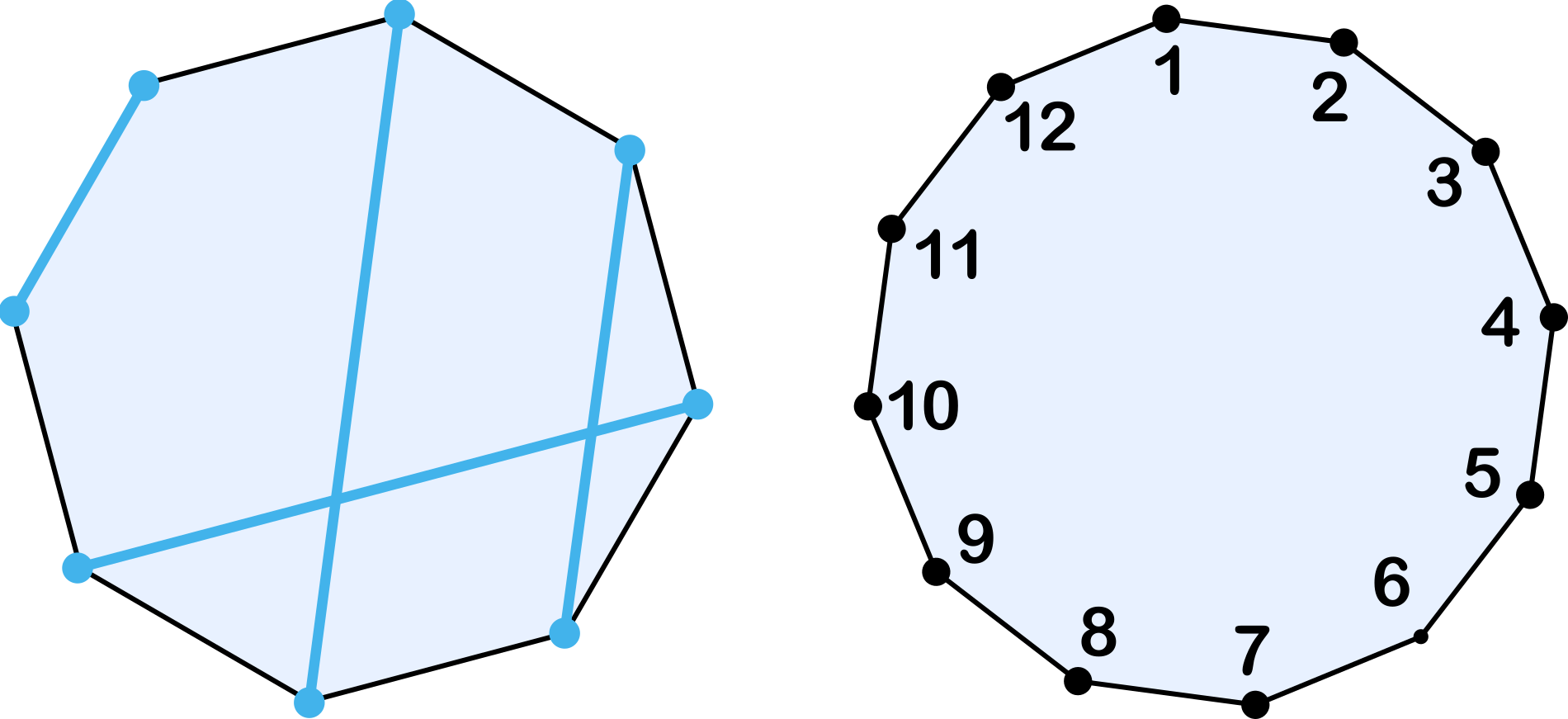
Nota. El mismo razonamiento prueba que es imposible el emparejamiento para polígonos de $8n+4$ vértices. ¿Es posible emparejar los vértices de un polígono de $8n$ lados? ¿Y los de un polígono de $4n+2$ lados?