Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Todos los problemas
XLI Olimpiada Matemática Española (fase local) — 2005
Sesión 1 — Viernes 21 de enero de 2005 (mañana)
Informar de error en enunciado Informar de procedencia del problema
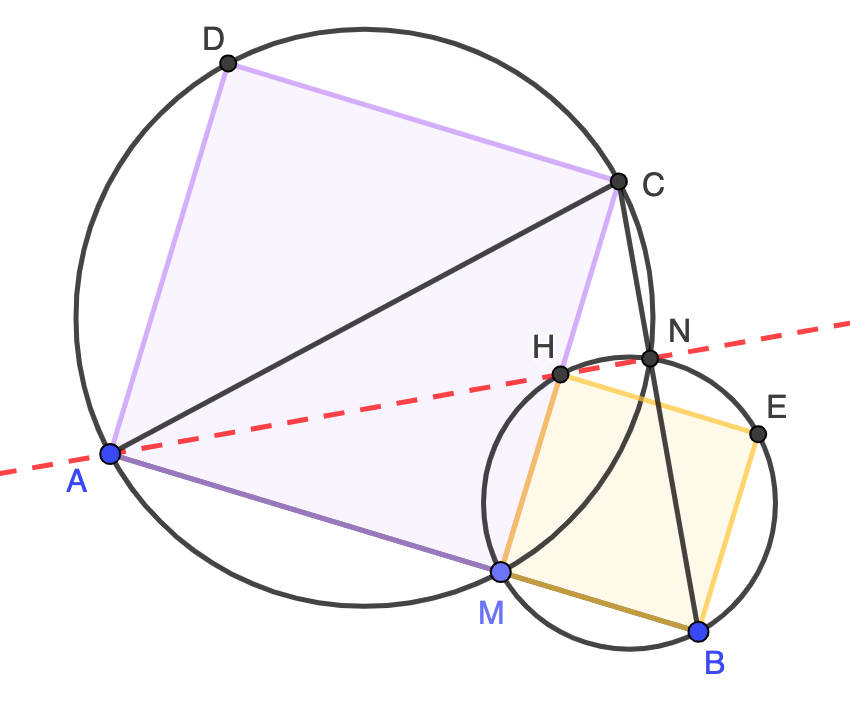
- Probar que los puntos $B$, $N$ y $C$ están alineados.
- Probar que el punto $H$ es el ortocentro del triángulo $ABC$.
- El ángulo $\angle HNB$ es recto ya que $HB$ es un diámetro de la circunferencia circunscrita al cuadrado $MBEH$. Por tanto, tanto $\angle HNB$ como $\angle HNC$ son rectos, lo que nos dice que $B$, $N$ y $C$ están alineados.
- Con lo ya demostrado, tenemos que $AN$ es la altura que pasa por $A$ en el triángulo $ABC$ y es obvio que $CM$ es la altura que pasa por el vértice $C$. Su intersección es $H$ y, por consiguiente, $H$ es el ortocentro de $ABC$.
Informar de error en enunciado Informar de procedencia del problema
- Si $x+y+z\geq 3$, ¿se verifica necesariamente que $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\leq 3$?
- Si $x+y+z\leq 3$, ¿se verifica necesariamente que $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\geq 3$?
La respuesta al apartado (b) es afirmativa. Para verlo, usamos la desigualdad entre las medias aritmética y armónica aplicada a los tres números positivos $x,y,z$: \[\frac{3}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}\leq \frac{x+y+z}{3}\leq 1\ \Longleftrightarrow\ \frac{1}{x}+\frac{1}{y}+\frac{1}{z}\geq 3.\]
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — Viernes 21 de enero de 2005 (tarde)
Para ver que el ángulo $x=\angle AMB$ es $45^\circ$, probaremos que su seno al cuadrado es $\frac{1}{2}$ (como $x\lt 90^\circ$, esto termina la demostración). Usando el teorema del seno en el triángulo $ABM$, tenemos que \begin{align*} \frac{c}{\mathrm{sen}(x)}=\frac{m}{\mathrm{sen}(105)}&\ \Longleftrightarrow\ \mathrm{sen}^2(x)=\frac{c^2\,\mathrm{sen}^2(105)}{m^2}=\frac{\frac{1}{2}\cdot\frac{2+\sqrt{3}}{4}}{\frac{2+\sqrt{3}}{4}}=\frac{1}{2}. \end{align*}
Informar de error en enunciado Informar de procedencia del problema
Nota. Da igual el color de las bolas iniciales siempre que al menos una de ellas sea negra (si empezamos con todas blancas no hay nada que demostrar).
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Sesión 3 — Sábado 22 de enero de 2005 (mañana)
Nota. Aunque la otra solución propuesta es más elegante, hay trucos que permiten manipular potencias de las raíces de un polinomio con cierta fluidez. En una prueba de olimpiada puede preferirse un cálculo más largo si estamos convencidos de que así saldrá la solución frente a buscar opciones más elegantes.
Informar de error en enunciado Informar de procedencia del problema
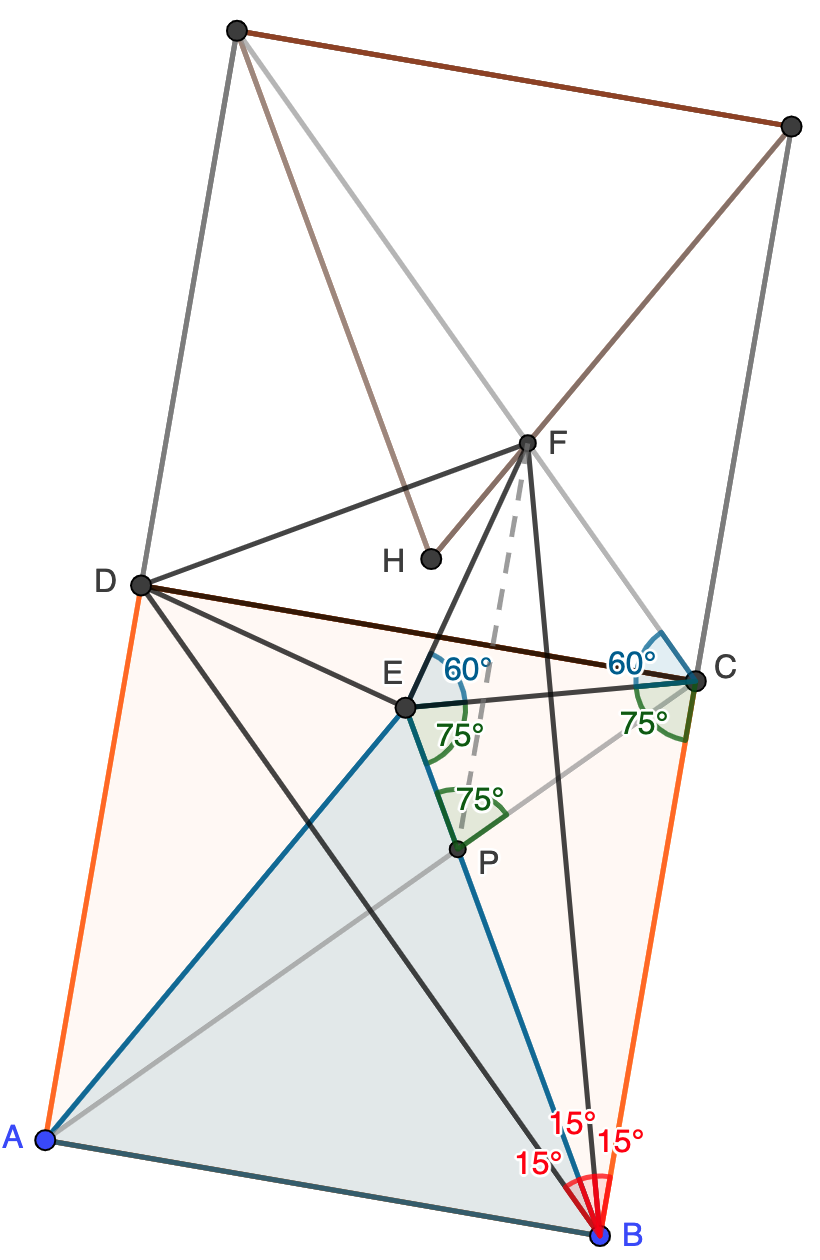
- El triángulo $CEF$ es equilátero.
- El triángulo $DEF$ es rectángulo e isósceles.
- El triángulo $BDF$ es isósceles.
- El triángulo $PDF$ es equilátero.
Que $CEF$ es equilátero implica que $EF=CE=DE$, ya que $CDE$ es claramente isósceles. Además, esto último nos dice que $\angle DEF=180-15-15=150$, con lo que $\angle DEF=150-60=90$. Tenemos entonces probado el apartado (b): $DEF$ es rectángulo e isósceles porque tiene dos lados iguales que forman un ángulo recto.
Ahora observamos que $\angle DEB=60+75=\angle FEB$, luego la recta $EB$ es la bisectriz interior del ángulo recto $\angle DEF$. Esta bisectriz es mediatriz del triángulo isósceles $DEF$, luego cualquier punto de $BE$ está a la misma distancia de $D$ que de $F$. En particular, el triángulo $BDF$ es isósceles y ya tenemos (c).
Tenemos que $PDF$ es isósceles por el mismo motivo, luego será suficiente ver que $\angle DFP=60$ y habremos terminado (hay realmente muchas formas de hacerlo). Como $\angle DBE=60-45=15$, tenemos que $\angle EBF=15$, luego también tenemos que $\angle FBC=90-45-15-15=15$. En otras palabras, $FB$ es bisectriz (y por tanto mediatriz) en el triángulo isósceles $CBE$, luego también lo es del triángulo equilátero $EFC$. Esto nos lleva a que $\angle EFB=\angle BFE=30$. Si trazamos ahora el segmento $PF$, que es paralelo a $BC$ por la simetría, tenemos que $\angle PFB=\angle CBF=15$ por ser ángulos internos alternos, luego $\angle DFP=45+15=60$ como queríamos probar.
Informar de error en enunciado Informar de procedencia del problema
- Si $x\neq\frac{1}{2}(1\pm\sqrt{5})$, entonces tras simplificar todos los factores comunes obtenemos que $f(x)=1-x^2$.
- Para el caso $x=\frac{1}{2}(1\pm\sqrt{5})$, sustituimos estos valores en la ecuación inicial, lo que nos da el siguiente sistema lineal en las incógnitas $a=\frac{1}{2}(1-\sqrt{5})$ y $b=\frac{1}{2}(1-\sqrt{5})$: \[\left\{\begin{array}{l}2a+(3+\sqrt{5})b=-5-\sqrt{5},\\ (3-\sqrt{5})a+2b=-5+\sqrt{5}\end{array}\right.\] Es fácil ver que es compatible indeterminado y que podemos despejar \[b=\frac{-5+\sqrt{5}-(3-\sqrt{5})a}{2},\] de forma que $a$ es un parámetro real arbitrario.
Nota. Este problema se ha marcado con 2,5 estrellas porque es realmente fácil omitir el caso $x=\frac{1}{2}(1\pm\sqrt{5})$ y decir que $f(x)=1-x^2$ para todo $x\in\mathbb{R}$ (este fallo está incluso en la solución oficial), que se corresponde con el caso $a=\frac{-1+\sqrt{5}}{2}$.
Informar de error en enunciado Informar de procedencia del problema
Sesión 4 — Sábado 22 de enero de 2005 (tarde)
- Si $b=1$, las desigualdades quedan $46\lt 6a$ y $7a\lt 57$, es decir, $\frac{46}{6}\lt a\lt\frac{57}{7}$ que tiene por única solución entera $a=8$.
- Si $b=2$, queda $44\lt 6a$ y $7a\lt 54$, que no tiene soluciones enteras.
- Si $b=3$, queda $42\lt 6a$ y $7a\lt 51$, que no tiene soluciones enteras.
- Si $b=4$, queda $40\lt 6a$ y $7a\lt 48$, que no tiene soluciones enteras.
- Si $b=5$, queda $38\lt 6a$ y $7a\lt 45$, que no tiene soluciones enteras.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema