Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Todos los problemas
XXI Olimpiada Iberoamericana de Matemáticas — 2006
Sesión 1 — Guayaquil (Ecuador), 26 de septiembre de 2006
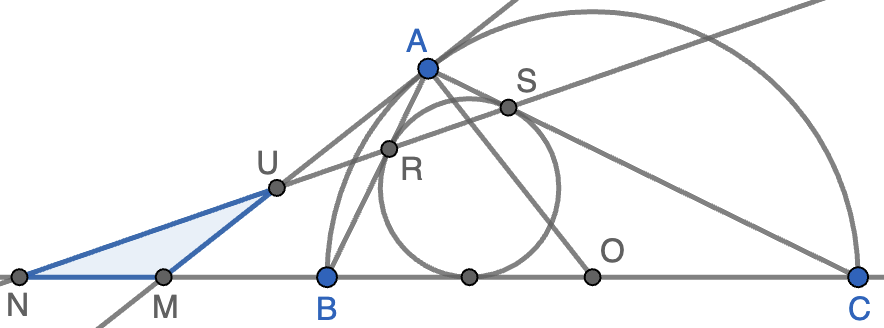
Informar de error en enunciado Informar de procedencia del problema
Para demostrar la primera desigualdad, para cada subíndice intermedio $1\lt i\lt n$, vamos a quedarnos solo con los sumandos $a_1-a_i$ y $a_i-a_n$, que suman $a_1-a_n=d$. Esto nos da una cota $s\geq (n-2)d$ ya que hay $n-2$ subíndices intermedios. Si también le añadimos la diferencia $a_1-a_n=d$ entre el mayor y el menor, tenemos que $s\geq (n-1)d$ y la igualdad se alcanza si y sólo cualquier otra diferencia de dos términos es nula, es decir, cuando dados dos subíndices intermedios $1\lt i,j\lt n$, se cumple que $a_i-a_j=0$. Tenemos, por tanto, que la igualdad se alcanza si y solo si $a_2=a_3=\ldots=a_{n-1}$.
Para la otra desigualdad, vamos a calcular $s$ explícitamente. En la suma $s$, un término $a_k$ se suma $n-k$ veces (una por cada subíndice $k\lt j\leq n$) y se resta $k-1$ veces (una por cada subíndice $1\leq j\lt k$). Por lo tanto, tenemos que \begin{align*} s&=(n-1)a_1+(n-2)a_2+(n-3)a_3+\ldots+1a_{n-1}+0a_n\\ &\qquad -0a_1-1a_2-2a_3-\ldots-(n-2)a_{n-1}-(n-1)a_n\\ &=(n-1)a_1+(n-3)a_2+(n-5)a_3+\ldots+(5-n)a_{n-2}+(3-n)a_{n-1}+(1-n)a_n. \end{align*} Distinguimos dos casos:
- Si $n=2k$ es par, entonces hay $k$ coeficientes positivos y $k$ negativos. Si dejamos fijos $a_1$ y $a_n$, la suma $s$ será menor o igual que si tomamos $a_1=a_2=\ldots=a_k$ y $a_{k+1}=a_{k+2}=\ldots=a_n$ (maximizamos los términos con coeficiente positivo y minimizamos los que tienen coeficiente negativo). Esto nos dice que \[s\leq ((2k-1)+(2k-3)+\ldots+1)(a_1-a_n)=k^2d=\tfrac{n^2}{4}d\] y la igualdad se alcanza si y sólo si la mitad de los números son iguales al menor y la otra mitad iguales al mayor.
- Si $n=2k+1$ es impar, entonces el coeficiente central que multiplica a $a_{k+1}$ es $0$, luego el valor de $a_{k-1}$ no influye en $s$. Haciendo un razonamiento similar al caso anterior, tenemos que \[s\leq (2k+(2k-2)+\ldots+2)(a_1-a_n)=(k^2+k)d=\tfrac{n^2-1}{4}d.\] Por tanto, se tiene que $s\lt\frac{n^2}{4}$ a menos que $d=0$, es decir, la igualdad se alcanza si y solo si todos los números son iguales.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — Guayaquil (Ecuador), 27 de septiembre de 2006
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema