Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
XXIV Olimpiada Iberoamericana de Matemáticas — 2009
Sesión 1 — Santiago de Querétaro (México), 22 de septiembre de 2009
Problema 856
OIM, 2009-P1
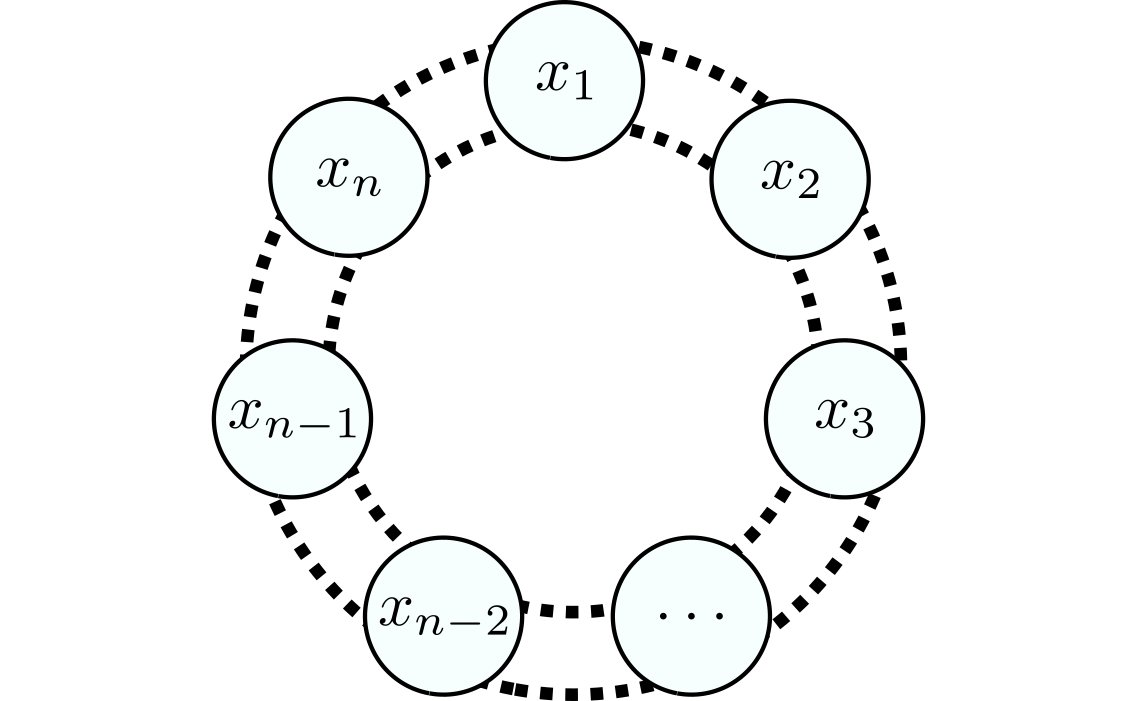
Sea $n\geq 3$ un entero. Supongamos que $n$ islas están ubicadas en un círculo y que entre cada dos islas vecinas hay dos puentes como en la figura.
Comenzando en la isla $x_1$, ¿de cuántas maneras se pueden recorrer los $2n$ puentes pasando por cada puente exactamente una vez?
pistasolución 1info
Pista. Se puede recorrer los puentes dándose la vuelta en algún $x_k$ o bien siempre girando en el mismo sentido. Halla por separado cuántas formas hay de hacer cada uno de esos recorridos. Ten en cuenta que puedes empezar girando en sentido horario o antihorario. Lo difícil de este problema es no dejarse ningún caso.
Solución. Una observación inicial importante que ayuda a centrar el problema, es que siempre se acaba en $x_1$. De esta manera, está claro que hay dos maneras esencialmente distintas de hacer el recorrido:
- Empezando en $x_1$, llegar hasta un cierto $x_k$, darnos la vuelta hasta regresar a $x_1$ y luego volver hasta $x_k$ por el otro lado y terminar de nuevo en $x_1$. Para llegar hasta $x_k$ en sentido horario tenemos $2^{k-1}$ posibilidades (equivale a elegir en cada isla uno de los dos puentes a la ida ya que a la vuelta tendremos que volver por el que no hemos elegido a la ida) y $2^{n-k+1}$ posibilidades para ir de $x_1$ a $x_k$ en sentido horario. Esto da $2^{k-1}2^{n-k+1}=2^n$ posibles caminos. Como esto ocurre para cada $k$ y podemos ir primero en sentido horario o primero en sentido antihorario, el número total de posibles caminos en este caso es $2n\cdot 2^n=2^{n+1}n$.
- Empezando en $x_1$ no nos damos la vuelta en ningún sitio sino que vamos girando siempre en sentido horario o antihorario dando dos vueltas a todo el círculo. Tendremos también $2^n$ posibles caminos en cada sentido de giro (ya que solo hay que elegir puente en la primera vuelta). Esto nos da $2^{n+1}$ posibilidades.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 857
OIM, 2009-P2
Para cada entero positivo $n$ se define $a_n=n+m$, donde $m$ es el mayor entero tal que $2^{2^m}\leq n2^n$. Determinar qué enteros positivos no aparecen en la sucesión $\{a_n\}$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 858
OIM, 2009-P3
Sean $C_1$ y $C_2$ dos circunferencias de centros $O_1$ y $O_2$ con el mismo radio y que se cortan en $A$ y en $B$. Sea $P$ un punto sobre el arco $AB$ de $C_2$ que está dentro de $C_1$. La recta $AP$ corta a $C_1$ en $C$, la recta $CB$ corta a $C2$ en $D$ y la bisectriz de $\angle CAD$ corta a $C_1$ en $E$ y a $C_2$ en $L$. Sea $F$ el punto simétrico a $D$ con respecto al punto medio de $PE$. Demostrar que existe un punto $X$ que satisface $\angle XFL=\angle XCD=30^\circ$ y $CX=O_1O_2$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — Santiago de Querétaro (México), 23 de septiembre de 2009
Problema 859
OIM, 2009-P4
Sea $ABC$ un triángulo con $AB\neq AC$. Sean $I$ el incentro de $ABC$ y $P$ el otro punto de intersección de la bisectriz exterior del ángulo $A$ con el circuncírculo de $ABC$. La recta $PI$ interseca por segunda vez al circuncírculo de $ABC$ en el punto $J$. Demostrar que los circuncírculos de los triángulos $JIB$ y $JIC$ son tangentes a $IC$ y a $IB$, respectivamente.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 860
OIM, 2009-P5
La sucesión $\{a_n\}$ está definida por
\[a_1=1,\qquad a_{2k}=1+a_k,\qquad a_{2k+1}=\frac{1}{a_{2k}},\quad \text{para todo }k\geq 1.\]
Demostrar que todo número racional positivo aparece exactamente una vez en esta sucesión.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 861
OIM, 2009-P6
Alrededor de una circunferencia se marcan $6000$ puntos y cada uno se colorea con uno de $10$ colores dados, de manera tal que entre cualesquiera $100$ puntos consecutivos siempre figuran los $10$ colores. Hallar el menor valor $k$ tal que, para toda coloración de este tipo, existen $k$ puntos consecutivos entre los cuales figuran los $10$ colores.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre