Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Todos los problemas
XLVI Olimpiada Matemática Española (fase local) — 2010
Sesión 1 — Viernes 15 de enero de 2010 (mañana)
- Si $n$ es impar, entonces la suma de los elementos de $I_n$ es impar, luego no se puede descomponer en dos subconjuntos disjuntos con la misma suma $S$ (la suma de todos los elementos de $I_n$ sería $2S$, que es par).
- Si $n$ es múltiplo de $4$, entonces sí se puede. Una forma de hacerlo es emparejar el primero con el último, el segundo con el penúltimo y así sucesivamente. Se forma así un número par de parejas con la misma suma cada una de ellas. Bastará entonces unir la mitad de las parejas por un lado y la otra mitad por otro para formar los dos subconjuntos.
- Si $n$ es par pero no múltiplo de $4$, tenemos que $I_2=\{1,3\}$ no se puede pero $I_6=\{1,3,5,7,9,11\}$ se puede descomponer en $\{1,3,5,9\}$ y $\{7,11\}$. Para todo número de la forma $4k+6$ con $k\geq 1$, podemos separar los seis primeros elementos de $I_n$ de la misma forma que los de $I_6$ y luego emparejar los $4k$ restantes (el primero con el último, el segundo con el penúltimo,...) en $2k$ parejas de la misma suma. Entonces, $I_n=A\cup B$, siendo $A$ el conjunto unión de $k$ parejas con $\{1,3,5,9\}$ y $B$ igual a la unión de $\{7,11\}$ con las otras $k$ parejas.
Deducimos de todo esto que los valores de $n$ para los que $I_n$ se descompone en dos subconjuntos disjuntos de la misma suma son los pares mayores o iguales que $4$.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Nota. $\lfloor x\rfloor$ denota la parte entera de un número real $x$.
- Si $n=6k$, entonces $\lfloor\frac{n}{2}\rfloor=\lfloor 3k\rfloor=3k$ y $\lfloor\frac{2n}{3}\rfloor=\lfloor 4k\rfloor=4k$, luego la ecuación queda $7k=6k+335$, cuya solución es $k=335$. Tenemos así que $n=6\cdot 335=2010$.
- Si $n=6k+1$, entonces $\lfloor\frac{n}{2}\rfloor=\lfloor 3k+\frac{1}{2}\rfloor=3k$ y $\lfloor\frac{2n}{3}\rfloor=\lfloor 4k+\frac{2}{3}\rfloor=4k$, luego la ecuación queda $7k=6k+336$, cuya solución es $k=336$. Tenemos así que $n=6\cdot 336+1=2017$.
- Si $n=6k+2$, entonces $\lfloor\frac{n}{2}\rfloor=\lfloor 3k+1\rfloor=3k+1$ y $\lfloor\frac{2n}{3}\rfloor=\lfloor 4k+\frac{4}{3}\rfloor=4k+1$. La ecuación queda $7k+2=6k+337$, luego $k=335$ y $n=6\cdot 335+2=2012$.
- Si $n=6k+3$, entonces $\lfloor\frac{n}{2}\rfloor=\lfloor 3k+\frac{3}{2}\rfloor=3k+1$ y $\lfloor\frac{2n}{3}\rfloor=\lfloor 4k+2\rfloor=4k+2$. La ecuación queda $7k+3=6k+338$, luego $k=335$ y $n=6\cdot 335+3=2013$.
- Si $n=6k+4$, entonces $\lfloor\frac{n}{2}\rfloor=\lfloor 3k+2\rfloor=3k+2$ y $\lfloor\frac{2n}{3}\rfloor=\lfloor 4k+\frac{8}{3}\rfloor=4k+2$. La ecuación queda $7k+4=6k+339$, luego $k=335$ y $n=6\cdot 335+4=2014$.
- Si $n=6k+5$, entonces $\lfloor\frac{n}{2}\rfloor=\lfloor 3k+\frac{5}{2}\rfloor=3k+2$ y $\lfloor\frac{2n}{3}\rfloor=\lfloor 4k+\frac{10}{3}\rfloor=4k+3$. La ecuación queda $7k+5=6k+340$, luego $k=335$ y $n=6\cdot 335+5=2015$.
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — Viernes 15 de enero de 2010 (tarde)
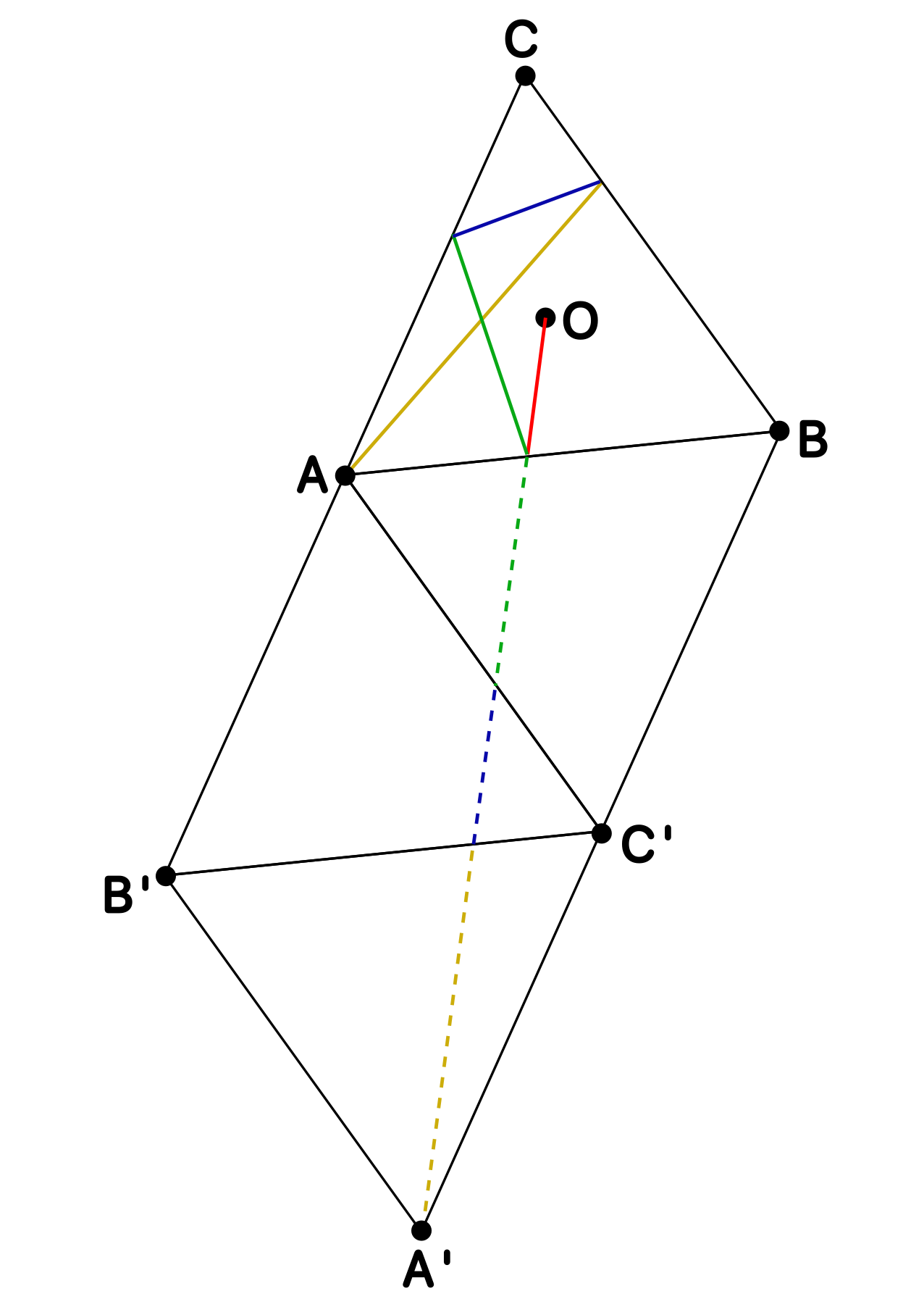
Nota. Cuando un rayo se refleja en un lado, los ángulos de entrada (incidencia) y salida (reflexión) coinciden.

Para ello, observamos que $OBA'$ es un triángulo rectángulo ya que $OB$ es una altura del triángulo equilátero y $BA'$ es paralela al lado opuesto. Además, se tiene que $OB=\frac{2}{3}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$ (dos tercios de la altura) y $BA'=2$ (dos veces el lado), luego el teorema de Pitágoras nos da la distancia que buscamos: \[OA'=\sqrt{\left(\tfrac{\sqrt{3}}{3}\right)^2+2^2}=\frac{\sqrt{39}}{3}.\]
Informar de error en enunciado Informar de procedencia del problema
- Si $ab=44$, entonces tenemos la suma $a+b=5$ y el producto $ab=44$, lugo podemos despejar $a$ y $b$ como las soluciones de la ecuación de segundo grado $x^2-5x+44=0$. Esta ecuación no tiene soluciones reales.
- Si $ab=6$, entonces $a$ y $b$ son las soluciones de la ecuación de segundo grado $x^2-5x+6=0$, es decir, $(a,b)=(2,3)$ o bien $(a,b)=(3,2)$. Como $x=b^4$, tenemos las soluciones $x=16$ y $x=81$, que claramente verifican la ecuación inicial.
Informar de error en enunciado Informar de procedencia del problema
Nota. Si el primer jugador pone un $1$ en lugar de $-1$ en el término independiente, entonces es el segundo jugador el que tiene la estrategia ganadora. Para verlo, tomamos la factorización \[(x-1)(x+1)(x^2+ax-1)=x^4+ax^3-2x^2-ax+1.\] Si el segundo juega un $-2$ en el término de $x^2$, en su segundo turno solo tendrá que poner lo opuesto a lo que haya puesto el primer jugador en su segundo turno.
Informar de error en enunciado Informar de procedencia del problema
Sesión 3 — Sábado 16 de enero de 2010 (mañana)
- Demuestra que se pueden colocar siete fichas, cada una en una casilla distinta, de forma que al eliminar dos filas y dos columnas cualesquiera, siempre quede alguna ficha sin eliminar.
- Demuestra que si colocamos sólo seis fichas, siempre pueden eliminarse dos filas y dos columnas de forma que todas las fichas sean eliminadas.
Informar de error en enunciado Informar de procedencia del problema
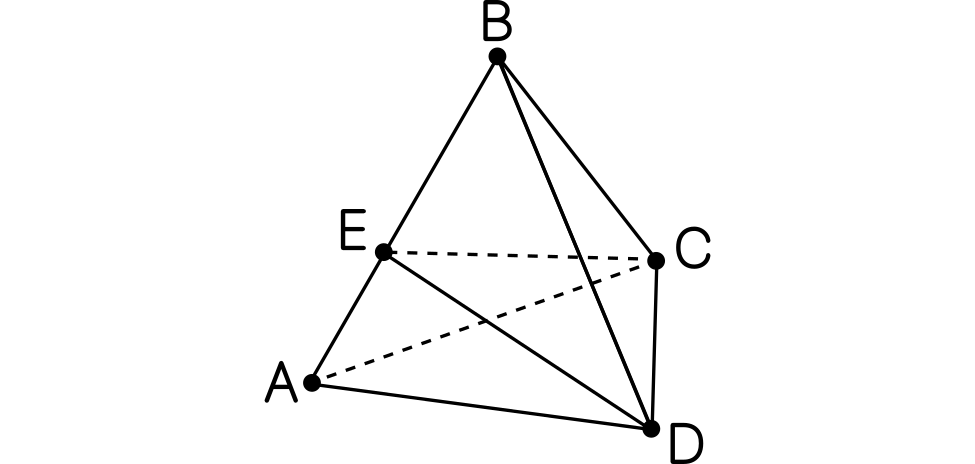
Nota. Usando el seno en lugar de la tangente, también puede razonarse de forma similar que lo que hay que minimizar es la longitud de $CE$, lo que nos lleva a que ha de ser perpendicular a $AC$ y $E$ tiene que ser el punto medio.
Informar de error en enunciado Informar de procedencia del problema
- Encontrar un conjunto especial de tres elementos.
- ¿Existe un conjunto de especial de cuatro números en progresión aritmética?
Informar de error en enunciado Informar de procedencia del problema
Sesión 4 — Sábado 16 de enero de 2010 (tarde)
casos favorables entre casos posibles.
Denotamos por $H$ a las hayas y por $A$ a los otros árboles (robles o encinas). Para que no estén consecutivas, tendremos que poner al menos un árbol entre cada haya: \[\_\ H\ A\ \_\ H\ A\ \_\ H\ A\ \_\ H\ A\ \_\ H\ \_\] aunque nos quden seis huecos marcados con $\_$ para poner otras tres $A$. Estas se podrán poner libremente en uno de los seis huecos, lo que nos da un total de $6^3$ configuraciones. Para cada una de ellas, podemos permutar las $H$ y permutar las $A$ libremente, lo que nos da un total de $5!\cdot 7!$ casos posibles por cada una de las $6^3$ configuraciones. La probabilidad que buscamos es, por lo tanto, \[\frac{6^3\cdot 5!\cdot 7!}{12!}=\frac{3}{11}.\]
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Nota. En este problema, la notación $\overline{xy}$ representa el número natural que tiene $x$ decenas e $y$ unidades, siendo $x,y\in\{0,1,2,3,4,5,6,7,8,9\}$.
Por lo tanto, $|r-50|$ y $|s-1|$ son iguales a $1$, $10$, $49$ o $50$. Obviamente, no puede ser $|r-50|=50$ ni $r-50=-49$ porque no se cumpliría que $10\leq r\leq 99$. Tenemos así cinco soluciones (observemos que en cada una de ellas sólo hay un valor posible de $s$ porque el otro, para el otro signo en el valor absoluto, no cumple que $0\leq s\leq 99$):
- Si $r=49$, entonces $s=51$, lo que nos da la solución $4951$.
- Si $r=51$, entonces $s=49$, lo que nos da la solución $5149$.
- Si $r=40$, entonces $s=50$, lo que nos da la solución $4050$.
- Si $r=60$, entonces $s=50$, lo que nos da la solución $6050$.
- Si $r=99$, entonces $s=11$, lo que nos da la solución $9911$.
Nota. Si permitimos que $a=0$, con el mismo razonamiento también tenemos las soluciones con $r=0$ (que implica $s=0$ o $s=2$) y con $r=1$ (que implica $s=11$), luego también tendríamos los números $0000$, $0002$ y $0111$.
Informar de error en enunciado Informar de procedencia del problema