Los años recientes se han podido expresar como sumas, restas y multiplicaciones de números con un mismo dígito; por ejemplo:
\begin{align*}
2009&=7\times 7\times 7\times 7-7\times 7\times 7-7\times7,\\
2010&=66\times 6\times 6-66\times 6+6\times 6-6.
\end{align*}
¿Se puede hacer lo mismo con el $2011$ sin repetir sumandos iguales? Por ejemplo, no es admisible escribir $2011=1+1+\ldots$
pistasolución 1info
Pista. Observa que el dígito no puede ser otro que $1$.
Solución. La respuesta es afirmativa. Por ejemplo, tenemos que
\[2011 = 1111\cdot 1111 - 1111\cdot 111\cdot 11 + 111\cdot 111\cdot 11 - 111\cdot 111 + 1111 - 111 + 11.\]
Nota. Aunque parezca muy sofisticada la solución, se puede llegar a ella tras diversas pruebas. En primer lugar, los números obtenidos de esta forma son múltiplos del dígito que usamos en el proceso. Como $2011$ no es divisible entre $2$, $3$, $5$ o $7$ (en realidad, $2011$ es primo), el único dígito que podría funcionar es el $1$. Como multiplicar por $1$ no tiene efecto, el problema se reduce a decidir si $2011$ se escribe como suma o diferencia de números que son producto con factores $11,111,1111,\ldots$ más o menos posiblemente un 1. Por otro lado, hay que tener en cuenta que en la olimpiada tenemos tiempo para hacer pruebas. Esta solución la hemos obtenido con el siguiente razonamiento: primero nos damos cuenta de que $1011=1111-111+11$ y nos queda obtener el $1000$ restante con factores más grandes. Empezando por $1111\cdot 1111=1234321$ restamos $1111\cdot 111\cdot 11=1356531$ para eliminar las unidades de millón, luego sumamos $111\cdot 111\cdot 11=135531$ para eliminar las centenas de millar, luego restamos $111\cdot 111=12321$ para eliminar las decenas de millar, números que hemos calculado previamente. Por un golpe de suerte, hemos obtenido el resultado $1000$ deseado (aunque puede razonarse que es así trabajando módulo $1000$).
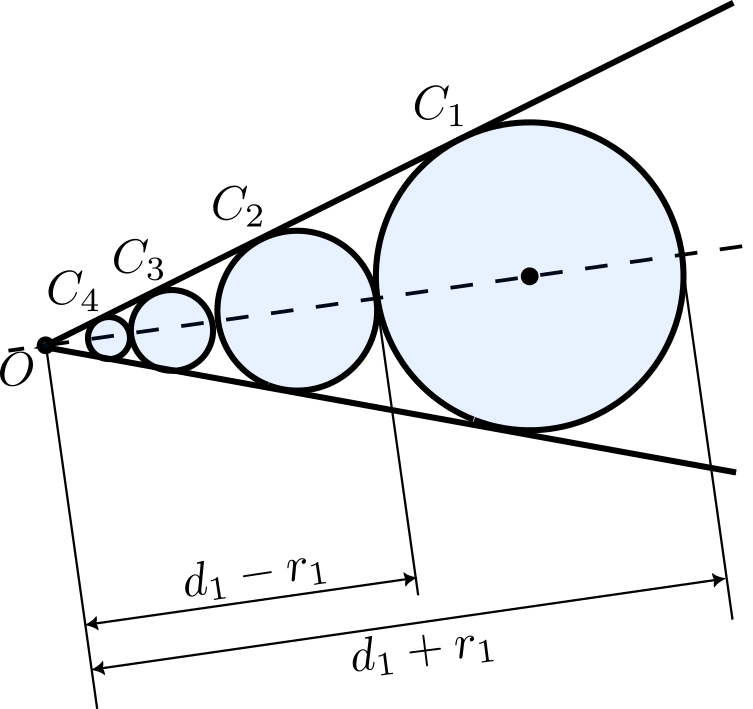
Dos semirrectas tienen su común origen en el punto $O$. Se considera una
circunferencia $C_1$ tangente a ambas semirrectas cuyo centro está situado
a distancia $d_1$ de $O$ y cuyo radio es $r_1$. Se construyen sucesivamente las circunferencias $C_n$, de modo que $C_n$ es tangente a las semirrectas, tangente exterior a $C_{n−1}$ y tal que la distancia de su centro a $O$, $d_n$, es menor que $d_{n−1}$ para $n\gt 1$. Halla la suma de las áreas de los círculos limitados por las circunferencias $C_n$ para todo $n$ en función de $r_1$ y $d_1$.
pistasolución 1info
Pista. Date cuenta de que existe una homotecia que lleva $C_k$ en $C_{k+1}$ para todo $k$. ¿Cuál es la razón de esta homotecia en términos de $r_1$ y $d_1$?
Solución. Sea $O_1$ el centro de $C_1$, que está sobre la bisectriz de las semirrectas dadas. Entonces, para pasar de la circunferencia $C_1$ a $C_2$, podemos hacer una homotecia de centro $O$ que lleva uno de los puntos de corte de $C_1$ con la bisectriz en el otro. Como el punto más alejado está a distancia $d_1+r_1$ y el más cercano a distancia $d_1-r_1$, la razón de la homotecia es $\lambda=\frac{d_1-r_1}{d_1+r_1}$. Como la homotecia transforma las áreas en un factor $\lambda^2$ y lleva cada circunferencia $C_k$ en $C_{k+1}$, tenemos que
\[\sum_{k=1}^n\mathrm{Area}(C_k)=\sum_{k=1}^n\lambda^{2k-2}\mathrm{Area}(C_1)=\frac{\pi r_1^2(1-\lambda^{2n+2})}{1-\lambda^2},\]
donde hemos usado la fórmula de la suma de los términos de una progresión geométrica. En el límite de esta suma cuando $n\to\infty$ el término $\lambda^{2n+2}$ desparece y el resultado es
\begin{align*}
\sum_{k=1}^\infty\mathrm{Area}(C_k)&=\frac{\pi r_1^2}{1-\lambda^2}=\frac{\pi r_1^2(d_1+r_1)^2}{(d_1+r_1)^2-(d_1-r_1)^2}\\
&=\frac{\pi r_1^2(d_1+r_1)^2}{4r_1d_1}=\frac{\pi r_1}{4d_1}(d_1+r_1)^2.
\end{align*}
La última cifra de $2009^{2011}$ es un nueve pero, ¿cuántos ceros preceden a ese nueve?
pistasolución 1solución 2info
Pista. Desarrolla $(2010-1)^{2011}$ usando el binomio de Newton. Otra alternativa es usar directamente el teorema de Euler-Fermat.
Solución. Podemos desarrollar la potencia usando el binomio de Newton si escribimos la base como $2010-1$. Además, trabajaremos módulo $1000$ porque solo nos van a interesar las tres últimas cifras. Tenemos que
\[2009^{2011}\equiv 9^{2011}\equiv(10-1)^{2011}\equiv-1+\binom{2011}{1}\cdot 2010-\binom{2011}{2}\cdot 10^2.\]
No tenemos que poner más términos del binomio porque a partir del siguiente nos quedan múltiplos de $1000$. De esta forma, podemos seguir desarrollando módulo $1000$ los números combinatorios para escribir finalmente:
\[2009^{2011}\equiv -1+11\cdot 10+55\cdot 10^2\equiv-391\equiv 609.\]
Por lo tanto, las tres últimas cifras son $609$ y concluimos que solo hay un cero que precede al nueve.
Nota. Si necesitáramos más cifras sólo habría que trabajar módulo una potencia de \(10\) más grande y añadir más términos al desarrollo del binomio. Esto quiere decir que no es relevante en el problema que solo haya que calcular tres dígitos.
Solución. Vamos a trabajar módulo $1000$ ya que solo nos van a interesar las tres últimas cifras. Vamos a usar el teorema de Euler-Fermat que nos dice que $a^{\varphi(n)}\equiv 1\ (\text{mod }n)$ si $a$ y $n$ son primos relativos y $\varphi(n)$ es la función de Euler. En nuestro caso, pondremos $a=9$ y $n=1000$, usando que $\varphi(1000)=\varphi(2^3\cdot 5^3)=2^2(2-1)\cdot 5^2(5-1)=400$. Por lo tanto,
\[2009^{2011}\equiv 9^{2011}=(9^{400})^5\cdot 9^{11}\equiv 9^{11}\ (\text{mod }1000).\]
Ahora bien, este último resto lo podemos calcular, observando que
\[9^2\equiv 81\ (\text{mod }1000),\quad 9^3\equiv 729\ (\text{mod }1000)\]
para luego calcular rápidamente
\[9^{11}\equiv 9^3\cdot 9^3\cdot 9^3\cdot 9^2\equiv 729\cdot 729\cdot 729\cdot 81\equiv 609\ (\text{mod }1000).\]
Aunque pueda parecer una cuenta larga, sólo nos tenemos que quedar con las últimas tres cifras en cada paso. Deducimos así que las tres últimas cifras de $2009^{2011}$ son $609$, con lo que la respuesta a la pregunta del enunciado es uno.
Calcula todos los números enteros $a$, $b$ y $c$ tales que $a^2=2b^2+3c^2$.
pistasolución 1info
Pista. Trabaja módulo $3$ y demuestra que los tres números deben múltiplos de $3$. Simplifica los factores $9$ comunes y vuelve a empezar.
Solución. Cualquier cuadrado es congruente con $0$ o $1$ módulo $3$. Por lo tanto, la ecuación solo es factible módulo $3$ si $a\equiv 0\ (\text{mod }3)$ y $b\equiv 0\ (\text{mod }3)$. Esto nos dice que podemos escribir $a=3x$ y $b=3y$ para ciertos $x,y\in\mathbb{Z}$. Sustituyendo, llegamos a que $9x^2=18y^2+3c^2$, luego $c^2=3x^2-6y^2$ debe ser también múltiplo de $3$, es decir, existe $z\in\mathbb{Z}$ tal que $c=3z$ y llegamos a otra solución de la misma ecuación: $x^2=2y^2+3z^2$.
Vamos a ver que esto implica que $a=b=c=0$. En efecto, si alguno de los tres números $a,b,c\in\mathbb{Z}$ es no nulo, entonces podríamos haber comenzado suponiendo que la solución $(a,b,c)$ es tal que la suma $a^2+b^2+c^2\gt 0$ es lo más pequeña posible (de entre todas las soluciones no nulas habrá una que cumpla esto), pero entonces $(x,y,z)$ es una solución con
\[x^2+y^2+z^2=\frac{1}{9}(a^2+b^2+c^2)\lt a^2+b^2+c^2,\] en contradicción con el hecho de que $a^2+b^2+c^2$ es mínimo. Esto es lo que se llama técnica del descenso infinito o principio de minimalidad.
Dos esferas de radio $r$ son tangentes exteriores. Otras tres esferas de radio $R$ son tangentes exteriores entre sí dos a dos. Cada una de estas tres esferas es además tangente exterior a las dos primeras. Encuentra la relación entre $R$ y $r$.
pistasolución 1info
Pista. Encuentra un triángulo rectángulo con vértices en los centros y los puntos de tangencia.
Solución. Sea $O$ el centro de una de las esferas de radio $r$, $C$ el centro de una de las esferas de radio $R$ y $T$ el punto de tangencia de las dos esferas de radio $r$. Por la simetría de la figura, es evidente que $OCT$ es un triángulo rectángulo con ángulo recto en $T$. Como $T$ es un punto de la esfera de centro $O$, tenemos que $OT=r$; por la tangencia de las esferas de centros $O$ y $C$, tenemos que $OC=R+r$; finalmente, como los centros de las esferas de radio $R$ forman un triángulo equilátero de centro $T$ y lado $2R$, se tiene que $CT$ es $\frac{2}{3}$ de la altura de dicho triángulo, es decir $CT=\frac{2}{3}\cdot\frac{\sqrt{3}}{2}\cdot 2R=\frac{2\sqrt{3}}{3}R$. El teorema de Pitágoras nos dice entonces que
\[OC^2=OT^2+CT^2\ \Longleftrightarrow\ (R+r)^2=r^2+\tfrac{4}{3}R^2\ \Longleftrightarrow\ 2Rr=\tfrac{1}{3}R^2\ \Longleftrightarrow\ R=6r.\]
Esta es la relación buscada (observemos que se ha descartado la solución $R=0$ ya que no es posible en este problema).
Encuentra todas las funciones $f:\mathbb{N}\to\mathbb{N}_0$ que sean crecientes y tales que $f(nm) = f(n) + f(m)$ para todo $n,m\in\mathbb{N}$.
Nota. Aquí, $\mathbb{N}_0$ denota el conjunto de los números naturales incluyendo el cero. La función $f$ es creciente cuando $f(n)\geq f(m)$ siempre que $n\gt m$.
pistasolución 1info
Pista. Aplica $f$ a los dos miembros de la desigualdad $(n-1)(n+1)\lt n\cdot n$ usando que $f$ es creciente.
Solución. Usando que $(n+1)(n-1)=n^2-1\lt n^2$, el crecimiento de $f$ y la condición del enunciado, podemos escribir
\[f(n-1)+f(n+1)=f(n^2-1)\leq f(n^2)=2f(n).\]
Esta condición, se puede reescribir como
\[f(n+1)-f(n)\leq f(n)-f(n-1),\qquad\text{para todo }n\in\mathbb{N}.\]
Por tanto, la diferencia entre dos términos consecutivos es positiva y decreciente. Debe llegar un momento en que esta diferencia sea una constante $a\geq 0$, momento a partir del cual la función se comporte como una progresión aritmética. Más rigurosamente, existe $n_0\gt 1$ tal que $f(n)=an+b$ para todo $n\geq n_0$, siendo $a,b\in\mathbb{Z}$ y $a\geq 0$.
Tomando $m,n\geq n_0$, se tiene que $mn\geq n_0$, luego
\[amn+b=f(mn)=f(n)+f(m)=a(m+n)+2b.\]
Como esta igualdad se cumple para infinitos valores de $m$ y $n$, tiene que ser $a=b=0$, es decir $f(n)=0$ para todo $n\geq n_0$. El problema ya está casi listo porque, por un lado, $f(1)=f(1\cdot 1)=f(1)+f(1)$ nos dice que $f(1)=0$ y, por otro lado, $f(2^r)=rf(2)$ tiene que ser cero para $r$ suficientemente grande tal que $2^r\gt n_0$, luego $f(2)$. Al ser $f(2)-f(1)=0$, tenemos que $f(n+1)=f(n)$ para todo $n\in\mathbb{N}$ y, por tanto, $f$ es la función constante $0$ (se comprueba trivialmente que cumple las condiciones del enunciado).
Sean $n_1$ y $n_2$ dos números naturales. Demuestra que la suma $\sqrt{n_1} + \sqrt[3]{n_2}$ es un número entero o un número irracional.
pistasolución 1info
Pista. Si fuera racional, despeja la raíz cúbica y eleva al cubo para eliminarla.
Solución. Supongamos que $\sqrt{n_1}+\sqrt[3]{n_2}$ es un racional $\frac{p}{q}$ y probaremos que debe ser entero. Para ello, despejamos la raíz cúbica y elevamos al cubo para eliminarla, esto es,
\[\sqrt[3]{n_2}=\frac{p}{q}-\sqrt{n_1}\ \Longleftrightarrow\ n_2=\frac{p^3}{q^3}-3\frac{p^2}{q^2}\sqrt{n_1}+3\frac{p}{q}n_1-n_1\sqrt{n_1}.\]
Agrupando los términos con raíz, llegamos a que
\[n_2=\left(\frac{p^3}{q^3}+3\frac{p}{q}n_1\right)-\left(n_1+3\frac{p^2}{q^2}\right)\sqrt{n_1}\ \Longleftrightarrow\ \sqrt{n_1}=\frac{n_2-\frac{p^3}{q^3}-3\frac{p}{q}n_1}{n_1+3\frac{p^2}{q^2}}.\]
Observemos que el denominador es un número positivo (no puede ser cero). Por lo tanto, $\sqrt{n_1}$ es un número racional, lo que nos dice que $n_1$ ha de ser un cuadrado perfecto (ver la nota). De esta manera, $\sqrt[3]{n_2}=\frac{p}{q}-\sqrt{n_1}$ también es racional, luego $n_2$ ha de ser un cubo perfecto (ver la nota) y $\sqrt[3]{n_1}+\sqrt{n_2}$ es entero.
Nota. Hemos usado el hecho muy conocido de que si $a$ y $n$ son números naturales y $\sqrt[n]{a}$ es racional, entonces $a$ es la potencia $n$-ésima de un entero. Esto se demuestra fácilmente escribiendo $\sqrt[n]{a}=\frac{r}{s}$ equivalentemente como $s^na=r^n$. Si ahora miramos en esta última ecuación el exponente de cualquier primo, el exponente en $a$ tiene que ser múltiplo de $n$.
Demuestra que en un triángulo se verifica: si $r$ es una recta que pasa por su baricentro y no pasa por ningún vértice, la suma de las distancias a dicha
recta de los vértices que quedan en un mismo semiplano es igual a la distancia del tercer vértice a dicha recta.
pistasolución 1solución 2info
Pista. Usa coordenadas y recuerda que las coordenadas del baricentro son la media aritmética de las coordenadas de los vértices.
Solución. En primer lugar, nos damos cuenta de que $r$ no es una mediana y deja un vértice a un lado y dos al otro. Supondremos que es el vértice $A$ el que deja a un lado y $B$ y $C$ al otro. Sea $M$ el punto medio de $BC$, $G$ el baricentro y $P$ y $Q$ los puntos de corte de $r$ con los lados $AB$ y $BC$, respectivamente, como se muestra en la figura. También trazamos segmentos perpendiculares a $r$ por $A$, $B$, $C$ y $M$, que tienen sus pies en $A'$, $B'$, $C'$ y $M'$, respectivamente.
Sabemos que el baricentro divide a la mediana $AM$ en dos segmentos tales que $AG=2GM$, luego el triángulo $AGQ$ tiene doble de área del triángulo $GQM$ (tiene la misma altura y base doble) y el triángulo $AGP$ tiene el doble de área que el triángulo $PGM$. Por tanto, el área de $APQ$ (en verde) es también el doble que la de $PQM$ (en azul). Podemos calcular el área de $APQ$ como $\frac{1}{2}AA'\cdot PQ$ y el área de $PQM$ como $\frac{1}{2}MM'\cdot PQ$. Ahora nos damos cuenta de que $MM'=\frac{1}{2}(BB'+CC')$ por el teorema de Thales ya que $BB',MM',CC'$ son paralelas que cortan a $r$ y $BC$ con $BM=CM$. Por lo tanto, el área de $PQM$ es $\frac{1}{4}(BB'+CC')PQ$, que debe ser la mitad de $\frac{1}{2}AA'\cdot PQ$, luego necesariamente $AA'=BB'+CC'$, que es lo que queríamos demostrar.
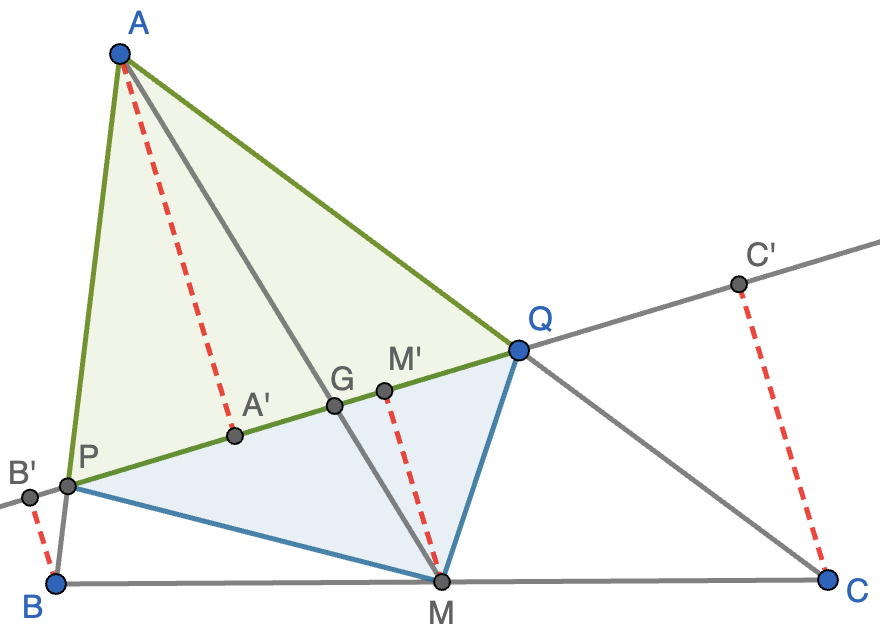
Solución. Vamos a trabajar en coordenadas, escribiendo los vértices del triángulo como $(x_1,y_1)$, $(x_2,y_2)$ y $(x_3,y_3)$. Las coordenadas del baricentro son la media aritmética, es decir,
\[\left(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3}\right).\]
Por tanto, una recta que pasa por este punto tendrá ecuación $Ax+By+C=0$, siendo $A,B,C\in\mathbb{R}$ tales que $A^2+B^2\neq 0$ y
\[A\frac{x_1+x_2+x_3}{3}+B\frac{y_1+y_2+y_3}{3}+C=0.\]
Esto último puede reescribirse como
\[\frac{Ax_1+By_1+C}{3}+\frac{Ax_2+By_2+C}{3}+\frac{Ax_3+By_3+C}{3}=0.\]
Como las tres fracciones suman cero, habrá dos de ellas con un signo y otra con el signo opuesto (no pueden ser cero porque la recta no pasa por ningún vértice). Supondremos que las dos primeras son del mismo signo y la tercera del signo opuesto, luego tomando valores absolutos, dividiendo por $\sqrt{A^2+B^2}$ y multiplicando por $3$, tenemos
\[\frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}}+\frac{|Ax_2+By_2+C|}{\sqrt{A^2+B^2}}=\frac{|Ax_3+By_3+C|}{\sqrt{A^2+B^2}}.\]
Cada fracción es la distancia desde el vértice correspondiente a la recta, luego el resultado está probado. El hecho de que dos fracciones tengan el mismo signo y otra el signo opuesto refleja el hecho de que la recta deja a dos puntos a un lado y al tercero al otro.
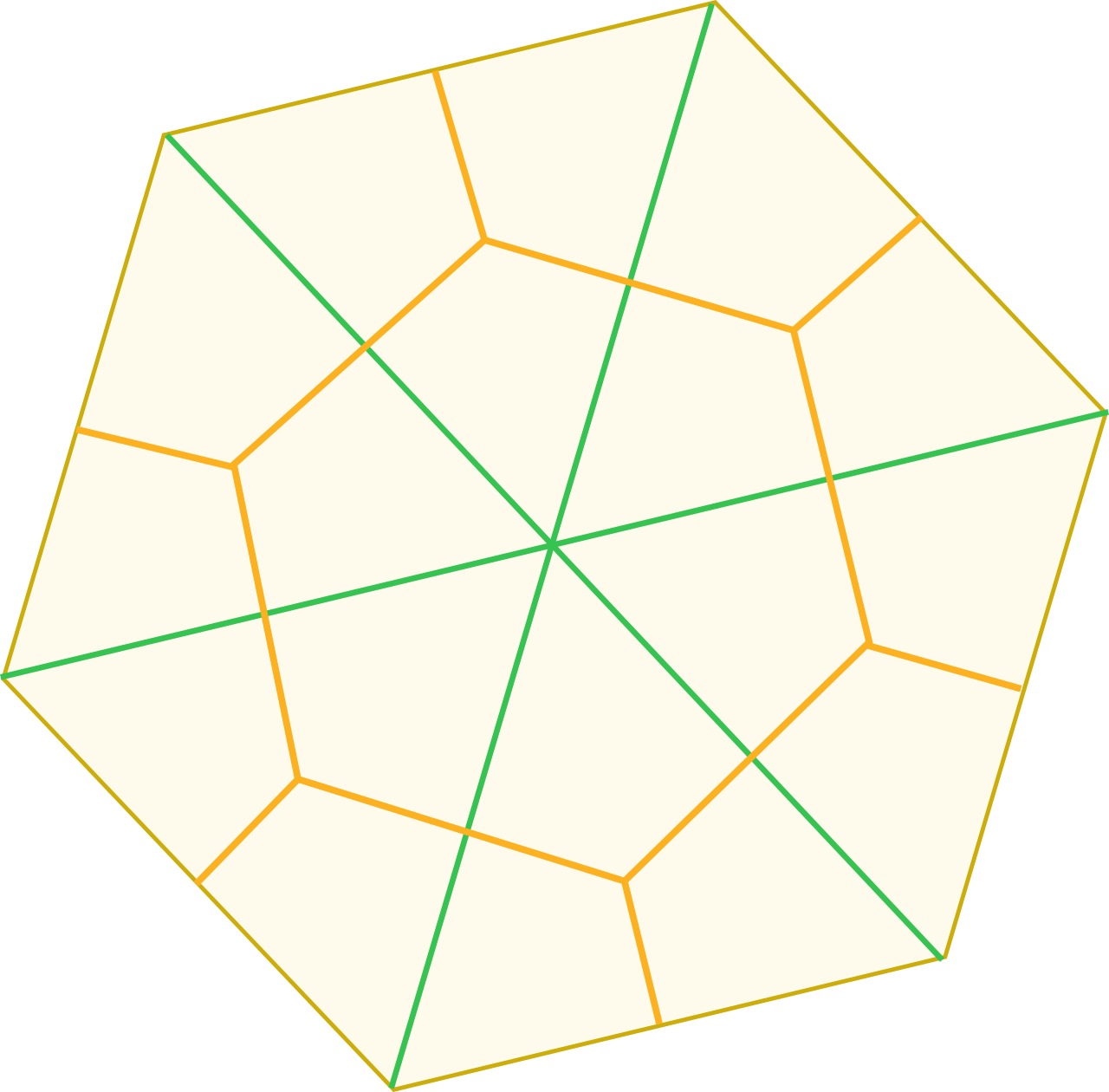
En un hexágono regular de lado unidad se sitúan $19$ puntos. Demuestra que
hay al menos un par de ellos separados por una distancia no mayor que $\frac{\sqrt{3}}{3}$.
pistasolución 1info
Pista. Descompón el hexágono en 18 regiones y utiliza el principio del palomar.
Solución. Consideramos la división del hexágono en 6 triángulos equiláteros de lado 1 indicada con líneas verdes en la figura y luego subdividimos cada triángulo en tres cometas uniendo su centro con los puntos medios de los tres lados, como se ha indicado con línea naranja. Esto nos da un total de 18 regiones y, por el principio del palomar, al menos 2 de los 19 puntos deben caer en una de ellas. Ahora bien, todas las regiones son congruentes entre sí y los puntos más distantes dentro de cada una de ellas son el centro y el vértice del triángulo equilátero en el que está contenida (véase la nota). Dicha distancia máxima es $\frac{2}{3}$ de la altura del triángulo, es decir, $\frac{2}{3}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$.
Halla todas las ternas de números enteros positivos $a\leq b\leq c$ de forma que no hay ningún primo que divida a los tres y que cada uno de ellos divida a la suma de los otros dos.
pistasolución 1info
Pista. Demuestra que $abc$ divide a $a+b+c$ (pero $abc$ por lo general es mucho mayor que $a+b+c$).
Solución. Supongamos que $a\mid b+c$, $b\mid a+c$ y $c\mid a+b$. Si $p$ es un primo que divide a $a$ y $b$, entonces divide a $b+c$ luego también divide a $c$. Este razonamiento nos dice que, si ningún primo divide a los tres, entonces tampoco puede dividir a dos, es decir, $a$, $b$ y $c$ son primos relativos dos a dos. Además, tenemos que $a$, $b$ y $c$ dividen a $a+b+c$, luego $abc$ divide a $a+b+c$ (por ser primos relativos). En partiular, se tiene que $abc\leq a+b+c\leq 3c$, con lo que $ab\leq 3$. Esto nos deja muy pocas posibilidades para el par $(a,b)$:
- Si $a=b=1$, las dos primeras condiciones $a\mid b+c$ y $b\mid a+c$ se cumplen siempre y la tercera $c\mid a+b=2$ nos dice que $c=1$ o $c=2$, luego tenemos las soluciones $(1,1,1)$ y $(1,1,2)$.
- Si $a=1$ y $b=2$, tenemos que $c\mid a+b=3$, luego $c=3$ ya que debe ser $b\geq c$. Se comprueba que $(1,2,3)$ también es solución.
- Si $a=1$ y $b=3$, entonces $c\mid a+b=4$ nos dice que $c=4$ para que sea $b\leq c$, pero no se cumple que $b\mid a+c$, luego no hay soluciones en este caso.
Deducimos así que la terna $(a,b,c)$ es $(1,1,1)$, $(1,1,2)$ o $(1,2,3)$.
En una reunión entre cuatro países de la ONU, digamos A, B, C y D, el país
A tiene el doble de representantes que el B, el triple que el C, y el cuádruple que el D. Se pretende distribuir a los representantes en mesas con el mismo número de personas en cada una. Sólo hay una condición: en cada mesa, cualquiera de los países debe estar en inferioridad numérica respecto de los otros tres juntos. ¿Cuántos representantes debe haber en cada mesa como mínimo?
Sin pistas
Sin soluciones
info


