Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
I Olimpiada Matemática de Andalucía — 2019
Sesión 1 — La Rábida, sábado 23 de febrero de 2019
Problema 634
Encontrar todas las soluciones del sistema de ecuaciones
\begin{align*}
ad &= b + c\\
bc &= a + d
\end{align*}
donde $a, b, c, d$ son enteros positivos tales que $a\lt b\lt c \lt d$.
pistasolución 1info
Pista. Observa que $b$ y $c$ son soluciones de la ecuación de segundo grado $x^2-(b+c)x+bc=x^2-adx+a+d$ y el discriminante de esta ecuación debe ser un cuadrado perfecto.
Solución. Podemos ver el sistema como un sistema de ecuaciones con incógnitas $b$ y $c$ en el que conocemos su suma y su producto. Esto equivale a que $b$ y $c$ son las soluciones de la ecuación de segundo grado
\[0=(x-b)(x-c)=x^2-(b+c)x+bc=x^2-adx+a+d.\]
Dado que $b\lt c$, podemos calcular estas soluciones como
\[b=\frac{ad-\sqrt{a^2d^2-4a-4d}}{2},\qquad c=\frac{ad+\sqrt{a^2d^2-4a-4d}}{2}.\]
Como se trata de números enteros positivos, tenemos que $a^2d^2-4a-4d$ tiene que ser un cuadrado perfecto. Como es menor que $(ad)^2$, tendrá que ser menor o igual que $(ad-1)^2=a^2d^2-2ad+1$, es decir,
\[a^2d^2-4a-4d\leq a^2d^2-2ad+1\ \Leftrightarrow\ ad-2a-2d\leq 1\ \Leftrightarrow\ (a-2)(d-2)\leq 5.\]
Ahora bien, $d$ tiene que ser al menos tres unidades mayor que $a$ para que se cumpla que $a\lt b\lt c\lt d$. Con esto en mente, la desigualdad $(a-2)(d-2)\leq 4$ implica que $a\leq 3$ (si $a\geq 4$, entonces $d\geq 7$ y $(a-2)(d-2)\geq 10$).
Repitiendo todo el razonamiento anterior con $b$ y $c$ en lugar de $a$ y $d$, tenemos que $b\leq 3$. Como $a\lt b$. Esto da lugar a tres casos:
- Si $(a,b)=(1,2)$, el sistema inicial se escribe como $d=c+2$ y $2c=1+d$. Este sistema tiene solución única $(c,d)=(3,5)$.
- Si $(a,b)=(1,3)$, el sistema inicial se escribe como $d=c+3$ y $3c=1+d$, que tiene solución única $(c,d)=(2,5)$, pero no cumple que $b\lt c$.
- Si $(a,b)=(2,3)$, el sistema inicial se escribe como $2d=c+3$ y $3c=2+d$, que tiene solución única $(c,d)=(\frac{7}{5},\frac{11}{5})$, que no son números enteros.
Tenemos así que la única solución al problema es $(a,b,c,d)=(1,2,3,5)$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 635
En un tablero de ajedrez de tamaño $n\times n$ se escribe $1$ o $−1$ en cada una de sus casillas. Sea $a_k$ el producto de todos los números de la fila $k$, y sea $b_m$ el producto de todos los números de la columna $m$. Si $n=2019$, ¿Podría ocurrir que la suma $a_1+a_2+\ldots+a_n+b_1+b_2+\ldots+b_n$ sea cero? ¿Y si $n=2020$?
pistasolución 1info
Pista. Prueba que al cambiar de signo un elemento de la tabla no cambia el resto de la suma módulo $4$.
Solución. Llamamos $S=a_1+\ldots+a_n+b_1+\ldots+b_n$. Al cambiar de signo el elemento que está en la fila $i$ y la columna $j$, tenemos que $a_i$ y $b_j$ cambian de signo. Distingamos dos casos:
- Si $a_i$ y $b_j$ son los dos positivos, entonces pasan a ser los dos negativos y $S$ decrece $4$ unidades.
- Si $a_i$ y $b_j$ son los dos negativos, entonces pasan a ser los dos positivos y $S$ crece $4$ unidades.
- Si $a_i$ y $b_j$ tienen signos opuestos, entonces siguen teniendo signos opuestos y $S$ permanece igual.
Si $n=2020$, lo anterior no concluye nada ya que $2020\cdot 2=4040\equiv 0\ (\text{mod }4)$. Sin embargo, en este caso sí que puede ser $S=0$. Una forma de hacerlo es poner todos positivos en la tabla excepto la mitad de los elementos de una de las diagonales principales.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 636
Sea $ABC$ un triángulo acutángulo, $D$, $E$ y $F$ los pies de las alturas que pasan por $A$, $B$ y $C$, respectivamente. Sea $\Gamma$ la circunferencia de diámetro $AD$, que corta a los lados $AB$ y $AC$ en los puntos $X$ e $Y$, respectivamente. Si $P$ es la intersección de $XY$ con $AD$ y $Q$ la intersección de $AD$ y $EF$, demuestra que $P$ es el punto medio de $QD$.
pistasolución 1info
Pista. Demuestra que $XY$ es paralela a $EF$ y corta a $FD$ en su punto medio.
Solución. Sea $H$ el ortocentro del triángulo $ABC$. Como los ángulos $\angle AFH$ y $\angle AEH$ son rectos, tenemos que $AEFH$ es cíclico con diámetro $AH$ (circunferencia verde en la figura). Si hacemos la homotecia con centro en $A$ que lleva $H$ en $D$, esta circunferencia se transforma en $\Gamma$ ya que $AD$ es un diámetro de $\Gamma$. Esto nos dice que $F$ se transforma en $X$ y $E$ en $Y$, así como que $EF$ es paralela a $XY$, $XD$ es paralela a $CF$ y $DY$ paralela a $BE$. Trazamos la paralela a $AB$ que pasa por $D$ (en naranja en la figura), que corta a $CF$ en cierto punto $Z$. Por el paralelismo mencionado y porque $CF$ es la altura perpendicular a $AB$, obtenemos que $XDZF$ es un rectángulo. Ahora bien, usando el arco capaz en $\Gamma$, tenemos que
\[\angle FXY=\angle ADY=90-\angle DAC=\angle ACB.\] De forma similar, usando el arco capaz en la circunferencia circunscrita a $BDHF$ (que también es cíclico), tenemos que
\[\angle XFD=\angle BFD = \angle BHD=90-\angle EBC=\angle ACB.\]
Esto asegura que $XY$ es la diagonal del rectángulo $XDZF$ y, por tanto, corta a la otra diagonal $FD$ en su punto medio $M$. En otras palabras, el vértice $Z$ está sobre $XY$, cosa que no sabíamos inicialmente.
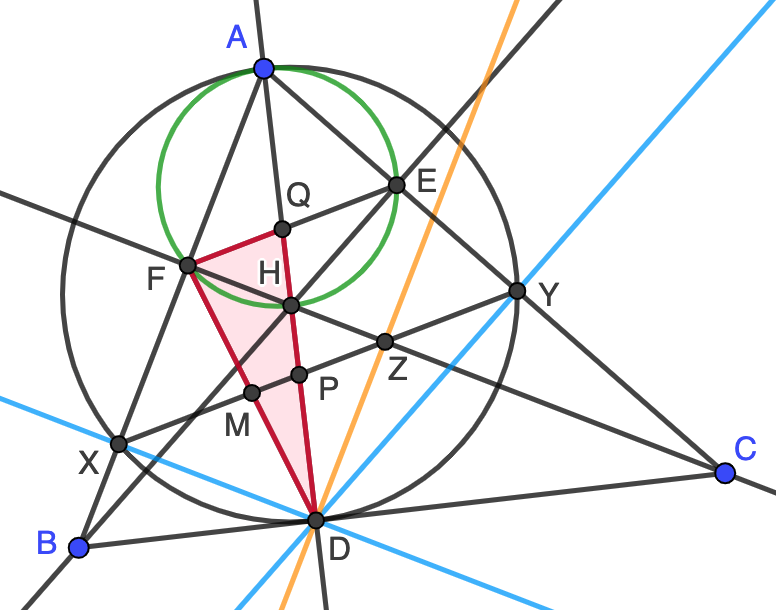
Finalmente, en el triángulo $FDQ$ (sombreado en rojo en la figura) la recta $XY$ es paralela al lado $FQ$ y pasa por el punto medio de $FD$, luego corta a $QD$ también en su punto medio, que es el punto $P$, y el problema está resuelto.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 637
Sean $k$, $m$ y $n$ enteros positivos tales que $k+m+1$ es un primo estrictamente mayor que $n+1$. Si $C_s$ denota el entero $s(s+1)$, demostrar que el producto
\[(C_{m+1} − C_k)(C_{m+2}-C_k)\cdots(C_{m+n}-C_k)\]
es divisible por $C_1C_2\cdots C_n$.
pistasolución 1info
Pista. Observa en primer lugar que puedes factorizar $C_{m+i}-C_k=(m+k+i+1)(m-k+i)$ y expresa el producto del enunciado en términos de números combinatorios.
Solución. En primer lugar, vamos a desarrollar los factores que aparecen en ese producto para obtener una expresión más sencilla. Observamos que
\begin{align*}
C_{m+i}-C_k&=(m+i+1)(m+i)-(k+1)k\\
&=(m+i)^2-k^2+m+i-k\\
&=(m+k+i)(m-k+i)+m-k+i\\
&=(m+k+i+1)(m-k+i).
\end{align*}
Por lo tanto, podemos agrupar factores para expresar
\begin{align*}
&\frac{(C_{m+1}-C_k)\cdots(C_{m+n}-C_k)}{C_1C_2\cdots C_n}\\
&\quad=\frac{(m+k+2)(m-k+1)\cdots(m+k+n+1)(m-k+n)}{1\cdot 2\cdot 2\cdot 3\cdots n(n+1)}\\
&\quad=\frac{(m+k+2)\cdots(m+k+n+1)(m-k+1)\cdots(m-k+n)}{n!(n+1)!}\\
&\quad=\frac{1}{m+k+1}\binom{m+k+n+1}{n+1}\binom{m-k+n}{n}.
\end{align*}
Los números combinatorios son enteros pero falta por ver que alguno de ellos es divisible por el primo $m+k+1$. Claramente lo es el primero de ellos dado que en
\[\binom{m+k+n+1}{n+1}=\frac{(m+k+1)(m+k+2)\cdots(m+k+n+1)}{(n+1)!}\]
el numerador es múltiplo de $m+k+1$ y el denominador no lo es ya que $n+1\lt m+k+1$ por hipótesis.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre