Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. El problema consiste en determinar si el número de participantes es par o impar, sabiendo que los estudiantes deben ser capaces de conocer sus notas a partir de las medias dadas. Llamemos $n$ al número de participantes y $x_1,\ldots,x_n$ a las notas en el orden que están sentados. Consideremos en primer lugar los siguientes casos:

• Si $n=2$, aunque no se considera en el enunciado, tenemos que sólo hay una media $m_1=\frac{x_1+x_2}{2}$ y muchas parejas de números ($x_1$ y $x_2$) producen la misma media, luego no se pueden determinar. Es importante darse cuenta de si los dos estudiantes tuvieran la nota máxima o mínima, entonces la media también sería la nota máxima o mínima y sí podrían determinarse, pero esta opción no es posible según el enunciado.
• En el caso $n=3$, si llamamos $m_1=\frac{x_1+x_2}{2}$, $m_2=\frac{x_2+x_3}{2}$ y $m_3=\frac{x_3+x_1}{2}$ a las tres medias, entonces se puede determinar $x_1=m_1+m_3-m_2$, $x_2=m_1+m_2-m_3$ y $x_3=m_2+m_3-m_1$. Estas fórmulas permiten a los tres participantes obtener su nota a partir de las tres medias.

Supongamos ahora que $n\geq 4$ y consideremos las notas consecutivas $x_1,x_2,x_3,x_4$. Tenemos entonces que \[\frac{x_1+x_2}{2}-\frac{x_2+x_3}{2}+\frac{x_3+x_4}{2}=\frac{x_1+x_4}{2},\] luego si eliminamos a los participantes en las posiciones $2$ y $3$, también conocemos las medias de los restantes (ahora las posiciones $1$ y $4$ son contiguas). Por tanto, resolver el problema para $n$ participantes es equivalente a resolverlo para $n-2$. Podemos repetir el proceso restando de dos en dos participantes hasta quedarnos con sólo dos o tres, en cuyo caso aplicamos los casos ya estudiados. Deducimos que si los estudiantes pueden hallar su nota, entonces $n$ es impar.

Nota. Esta es una solución dada por Samuel Gómez Moreno, proponente también del problema original.

Solución. Llamemos $x_i$ a la nota del estudiante $i$-ésimo (en el orden circular dado por la mesa) y $m_i$ a la media de $x_i$ y $x_{i+1}$, siendo $x_{n+1}=x_1$ y $n$ el número total de participantes.

• Si $n$ es impar, entonces usamos que $\sum_{i=1}^nx_i=\sum_{i=1}^nm_i$. Si llamamos a esta suma $S$, como $n$ es impar, podemos calcular \[x_1=S-(x_2+x_3+\ldots+x_n)=S-2(m_2+m_4+\ldots+m_{2n-1}).\] El resto de notas $x_2,x_3,\ldots,x_n$ pueden obtenerse por un procedimiento similar. Por tanto, $x_1,\ldots,x_n$ están determinados por las medias $m_1,\ldots,m_n$.
• Si $n$ es par, entonces a quienes se sientan en posiciones impares se les puede sumar una cantidad positiva $a$ y a quienes se sientan en las pares restarles $a$. Como este procedimiento no altera ninguna de las medias, deducimos que no pueden determinarse las notas a partir de estas. El número $a$ debe ser positivo y suficientemente pequeño para no pasar de la nota máxima ni de la nota mínima, y este número existe porque ningún participante tiene la nota máxima ni mínima.

Nota. Otra forma de descartar el caso en que $n$ es par es observar que las medias satisfacen $m_1+m_3+\ldots+m_{n-1}=m_2+m_4+\ldots+m_{n}$, luego el sistema lineal formado por las ecuaciones de la forma $x_i+x_{i+1}=2m_i$ tiene al menos un grado de libertad, esto es, $x_1,\ldots,x_n$ no están determinados.

Solución. Supongamos que $n$ es un cuadrado perfecto con todas sus cifras iguales y llamemos $a$ a la cifra de las unidades de $n$. Por un lado, si $n$ tiene todas sus cifras iguales, entonces $n=ab$ siendo $b$ un número formado sólo por unos. Por otro lado, los únicos valores posibles de $a$ son $0$, $1$, $4$, $5$, $6$ y $9$ (ya que depende sólo de la cifra de las unidades del número del que $n$ es cuadrado).

• No puede ser $a=0$ porque entonces sería $n=0\cdot b=0<10$.
• No puede ser $a=5$ porque entonces $b$ tendría otro factor $5$, pero claramente $b$ no es múltiplo de $5$.
• No puede ser $a=6$ por la misma razón ($b$ tendría otro factor $2$ pero no es un número par).

En el resto de casos $a=1$, $a=4$ y $a=9$, el propio $a$ es un cuadrado perfecto, luego tendremos que ver que el número $b$ formado sólo por unos no lo es. Por reducción al absurdo, si $b=m^2$ fuera un cuadrado perfecto, entonces la cifra de las unidades de $m$ será $1$ o $9$, luego $m=10k+1$ o bien $m=10k+9$ para cierto $k\geq 1$. Elevando al cuadrado tenemos que \[b=(10k+1)^2=100k^2+20k+1=20(5k^2+k)+1,\] luego $b$ es un múltiplo de $20$ más $1$, es decir, la cifra de las decenas de $b$ es par, lo que contradice que $b$ está formado sólo por unos. De la misma forma, \[(10k+9)^2=100k^2+180k+81=20(5k^2+9k+4)+1\] no puede estar formado sólo por unos.

Solución. Las dos últimas cifras de $n^2$ dependen exclusivamente de las dos últimas cifras de $n$. Esto se debe a que, si $n=100k+p$, donde $0\leq p\leq 99$ representa a las dos últimas cifras de $n$, entonces $n^2=100(100k^2+2kp)+p^2$.

Los únicos números naturales menores que $100$ cuyos cuadrados tienen repetida las cifras de las unidades y las decenas (y son no nulas) son $12$, $38$, $62$ y $88$, que cumplen que $12^2=144$, $38^2=1444$, $62^2=3844$ y $88^2=7744$. Hemos reducido el problema a buscar los números naturales $m$ tales que $m^2=44\ldots4=4\cdots 11\ldots1$. Esto exige que $\frac{m}{2}$ sea impar (ya que el cuadrado de un número par es par). Podemos escribir $\frac{m}{2}=2l+1$ para cierto número $l$, de donde $(2l+1)^2=11\ldots1$ o bien $4l(l+1)=11\ldots10$. Esto no es posible porque los múltiplos de $4$ tienen sus dos últimos dígitos $00$ o múltiplo de $4$, pero $10$ no es múltiplo de $4$.

Nota. Esta es una solución aportada por Samuel Gómez Moreno.

Solución. La condición de rectángulo áureo se puede reescribir como $b^2-bh-h^2=0$. Dividiendo por $h^2$, se tiene la ecuación de segundo grado $(\frac{b}{h})^2-\frac{b}{h}-1=0$ con incógnita $\frac{b}{h}$. Como el cociente de longitudes $\frac{b}{h}$ es positivo, sólo nos interesa la única solución positiva de esta ecuación, dada por \[\frac{b}{h}=\frac{1+\sqrt{5}}{2}.\qquad(\star)\] El área del rectángulo (representada en verde en la figura) es $A=bh$. Por otro lado, la circunferencia que pasa por los vértices tiene centro en el centro del rectángulo, luego su radio es la distancia entre dicho centro y uno de los vértices. El teorema de Pitágoras aplicado a un triángulo rectángulo de vértices el centro, un vértice y el punto medio de un lado nos dice que $r^2=(\frac{b}{2})^2+(\frac{h}{2})^2$. Por tanto, el área de la región roja es $A'=\pi r^2-A=\frac{\pi}{4}(b^2+h^2)-bh$. Tendremos que estudiar el signo de la diferencia $A-A'$. A la vista de la igualdad ($\star$), dividimos por $h^2$ y obtenemos \[\frac{A-A'}{h^2}=\frac{b}{h}-\frac{\pi}{4}\left(\!\left(\frac{b}{h}\right)^{\!2}\!\!+1\!\right)\!+\frac{b}{h}=\frac{1+\sqrt{5}}{2}-\frac{\pi}{4}\left(\!\left(\frac{1+\sqrt{5}}{2}\right)^{\!2}+1\!\right)\approx 0.19.\] Como este número es mayor que cero y $h^2>0$, deducimos que el área del rectángulo es mayor que la de la región restante del círculo.

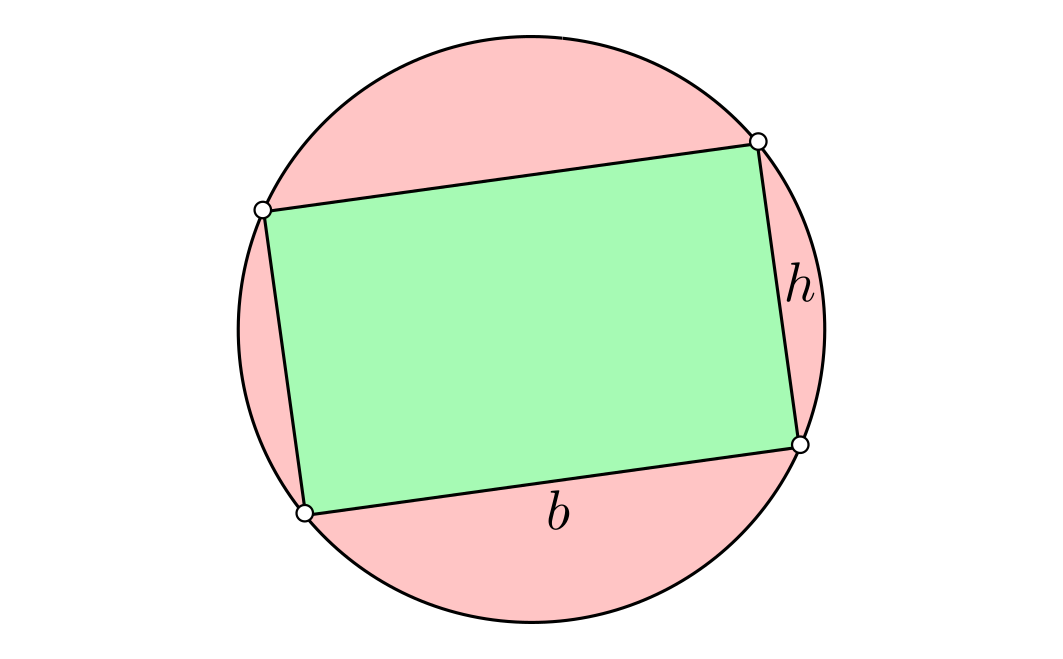
Nota. Otra opción para finalizar el ejercicio es darse cuenta de que el siguiente cociente es mayor que $1$: \[\frac{A}{A'}=\frac{\frac{b}{h}}{\frac{\pi}{4}((\frac{b}{h})^2+1)-\frac{b}{h}}=\frac{\frac{1+\sqrt{5}}{2}}{\frac{\pi}{4}((\frac{1+\sqrt{5}}{2})^2+1)-\frac{1+\sqrt{5}}{2}}\approx 1.32,\] donde hemos dividido numerador y denominador por $h^2$ para poder aplicar ($\star$). Una alternativa a esto último es suponer a lo largo de todo el razonamiento que $h=1$ haciendo previamente una homotecia.