Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 75
OIM, 1993-P4
Sea $ABC$ un triángulo equilátero y sean $M$ y $N$ puntos de $AB$ y $AC$, respectivamente, tales que el segmento $MN$ es tangente a la circunferencia inscrita de $ABC$. Demostrar que
\[\frac{AM}{MB}+\frac{AN}{NC}=1{.}\]
pistasolución 1info
Pista. Demostrar que el triángulo $AMN$ tiene perímetro igual al lado del triángulo equilátero inicial y, de ahí, sustituir $MB=MN+AN$ y $NC=MN+AM$.
Solución. Llamemos $T$ al punto de tangencia de $MN$ con la circunferencia inscrita y $\ell$ al lado del triángulo. Observemos que la longitud de $MT$ es igual a la del segmento que une $M$ con el punto medio del lado $AB$ por la propiedad de tangencia. Por tanto, $AM+MT=\frac{\ell}{2}$ y, de la misma forma, $AN+NT=\frac{\ell}{2}$, con lo que el perímetro del triángulo $AMN$ es exactamente $\ell$. Así, podemos escribir
\[\frac{AM}{MB}+\frac{AN}{NC}=\frac{AM}{MN+AN}+\frac{AN}{MN+AM}=\frac{AM^2+AN^2+MN(AN+AM)}{MN^2+MN(AN+AM)+AM\cdot AN}{.}\]
Por lo tanto, quisiéramos demostrar que $AM^2+AN^2=MN^2+AM\cdot AN$, pero esto se deduce de forma fácil del teorema del coseno aplicado al triángulo $AMN$ teniendo en cuenta que $\angle MAN=60^\circ$.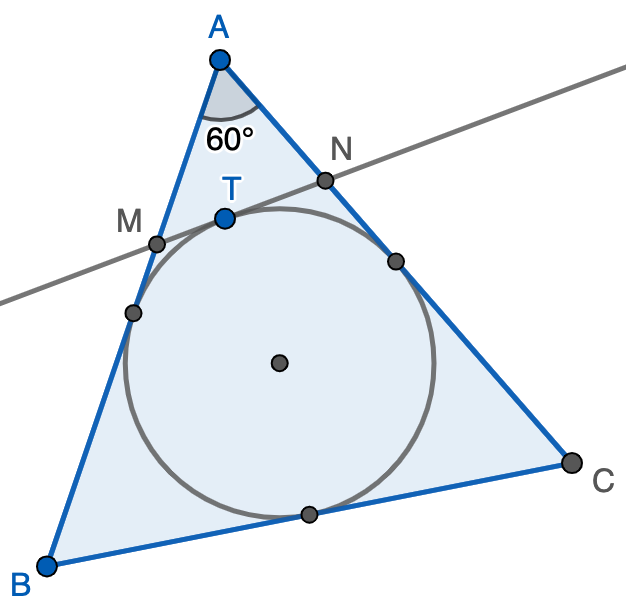

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 74
Sea $ABC$ un triángulo y $M$ el punto medio del lado $BC$. Si $r_1$ y $r_2$ son los inradios de los triángulos $ABM$ y $ACM$ respectivamente, demostrar que $r_1<2r_2$.
pistasolución 1info
Pista. Observa que el área del triángulo $ABM$ es la misma que la del triángulo $ACM$. ¿Qué relación existe entre el área de un triángulo, su perímetro y su radio inscrito?
Solución. El área del triángulo $ABM$ es la misma que la del triángulo $ACM$ ya que tienen la misma base $BM=CM$ y la misma altura. Por lo tanto, si llamamos $p_1$ y $p_2$ al semiperímetro de $ABM$ y $ACM$ respectivamente, tenemos que $r_1p_1=r_2p_2$ y deducimos que
\[\frac{r_1}{r_2}=\frac{p_2}{p_1}=\frac{AM+CM+AC}{AM+BM+MB}{.}\]
Así, tenemos que probar que $AM+CM+AC<2(AM+BM+AB)$ o, lo que es lo mismo, $AM+CM+2AB>AC$ y esta última desigualdad es consecuencia de la desigualdad triangular $AM+CM>AC$ (en el triángulo $ACM$) y de que $2AB>0$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 73
Demostrar que pueden tomarse \(2^k\) números del conjunto \(\{0,1,2,\ldots,3^k-1\}\), de forma que cualesquiera tres de ellos (distintos) no estén en progresión aritmética.
pistasolución 1info
Pista. Trabajar en base \(3\).
Solución. Escojamos aquellos números que, en base \(3\), se escriben únicamente con los dígitos \(0\) y \(1\). Está claro que hay \(2^k\) números satisfaciendo esta condición, luego bastará probar que no hay tres números de este tipo en progresión aritmética. En efecto, si \(a\lt b\lt c\) están en progresión aritmética, entonces \(2b=a+c\) pero, trabajando en base \(3\), \(2b\) sólo tiene dígitos 0 y 2 luego necesariamente \(a=c\) y, por tanto, \(a=b=c\), de donde no hay tres distintos en progresión aritmética.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 72
Demostrar que si \(n\in\mathbb{N}\) cumple que \((n-1)!+1\) es divisible entre \(n\), entonces \(n\) es un número primo.
pistasolución 1info
Pista. Demostrar que si \(n\) es compuesto entonces \((n-1)!+1\) no es divisible entre \(n\).
Solución. Probaremos el contrarrecíproco: si \(n\) es compuesto entonces \((n-1)!+1\) no es divisible entre \(n\), para lo que veremos que si \(n\neq 4\) y \(n=pq\) con \(1\lt p,q\lt n\), entonces \(n\) es un divisor de \((n-1)!\). Para probar esto último, si \(p\neq q\), tanto \(p\) como \(q\) son factores que aparecen en \((n-1)!\) ya que \(p\lt n\) y \(q\lt n\). Si, por el contrario, \(p=q\), entonces o bien \(p=2\), en cuyo caso \(n=4\) (caso que hemos aislado), o bien \(p\gt 2\) y \(n=p^2\gt 2p\), con lo que tanto \(p\) como \(2p\) aparecen en el desarrollo de \((n-1)!\) y, por tanto, \(n=p^2\) divide a \((n-1)!\). El caso \(n=4\) se comprueba directamente que verifica el enunciado.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 71
Demostrar que todo número entero \(n>6\) puede expresarse como suma de dos números naturales mayores que uno y primos entre sí.
pistasolución 1info
Pista. Distinguir si \(n\) es par o impar. Utilizar que cualquier divisor común a \(k\) y \(k+a\), también es divisor de \(a\).
Solución. Si \(n\) es impar, entonces es de la forma \(n=2k+1\) luego podemos expresarlo como \(k+(k+1)\), donde \(k\) y \(k+1\) son mayores que uno y primos entre sí. Si \(n\) es de la forma \(n=2k\) (es decir, es par), entonces \(n=(k-1)+(k+1)\). Si \(k-1\) y \(k+1\) son primos relativos, hemos terminado. En caso contrario, el único posible factor común a \(k-1\) y \(k+1\) es \(2\) en cuyo caso ambos son pares y podemos tomar \(n=(k-2)+(k+2)\), donde cualquier divisor de \(k-2\) y \(k+2\) divide a \(4\) pero \(k-2\) y \(k+2\) son ahora impares y, por tanto, primos relativos. Observemos que la condición \(n>6\) demuestra que todos los sumandos considerados son mayores que uno.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre