Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Existen métodos para construir cuadrados mágicos de cualquier orden. Por ejemplo, el método del rombo para los cuadrados mágicos permite poner los números del $1$ al $n^2$ en las casillas de una cuadrícula $n\times n$ para formar un cuadrado mágico de un orden $n$ impar, lo que se aplica a nuestro caso $n=2021$. Ahora es suficiente con multiplicar todas las entradas del cuadrado obtenido por $10000$ y sumarles $2022$, lo que no altera la propiedad de ser mágico.

Nota. Este no es un problema de estilo olímpico ya que requeriría el conocimiento de un método de obtención de cuadrados mágicos (conocimiento demasiado específico) o bien desarrollar dicho método en la solución (razonamiento demasiado complicado).

Solución. Sabemos que sólo se pueden alcanzar $12$ puntos, pongamos que se llaman $p_1,\ldots,p_{12}$ y que están ordenados en sentido de las agujas del reloj. En primer lugar, hay que observar que, a partir de cualquier punto $p_i$, avanzando un cierto número de veces una distancia $\ell_1$ se llega a cualquier otro $p_j$. Esto se deduce de que repetir dos veces la elección que ha generado los 12 puntos tiene que pasar otra vez por todos ellos. En segundo lugar, vamos a probar que los puntos están equiespaciados por reducción al absurdo, tomando dos puntos consecutivos $p_k$ y $p_{k+1}$ que definen el menor de los $12$ arcos en que $p_1,\ldots,p_{12}$ dividen a la circunferencia. Si $p_j$ y $p_{j+1}$ definieran un arco mayor, lo único que hay que hacer es, una vez estemos en $p_j$, repetir el mismo número de avances de longitud $\ell_1$ que llevan de $p_k$ a $p_{k+1}$: esto nos llevará de $p_j$ a un punto $p'_j$ que está estrictamente entre $p_j$ y $p_{j+1}$, lo que nos da la contradicción buscada.

Podemos entonces identificar el vértice $p_k$ con el número $k$ y $\ell_1$ y $\ell_2$ con enteros $6\lt\ell_1\lt \ell_2\lt 12$ tales que avanzar $\ell_i$ desde $p_k$ se corresponde con sumar $k+\ell_i$ módulo $12$. Los únicos números $\ell_1$ y $\ell_2$ que permiten pasar por los $12$ puntos son los primos relativos con $12$, lo que nos dice necesariamente que $\ell_1=7$ y $\ell_2=11$. Tenemos así que el radio de la mesa $r$ verifica $\ell_1=\frac{7}{12}\cdot 2\pi r$, lo que nos da $r=\frac{6\ell_1}{7\pi}$ y nos permite calcular su área a partir del dato $\ell_1$ que conoce Sophie: \[A=\pi r^2=\frac{36\pi\,\ell_1^2}{49}.\]

Nota. En realidad, no es necesario que se envíe el segundo Whatsapp puesto que, una vez se dibujan los 12 puntos, Sophie puede demostrar que son equidistantes con el argumento dado, y después sabe que avanzar la distancia $\ell_1$ supone 7 posiciones (porque ella puede contarlas, aunque nosotros no tengamos ese dato, es decir, ella sabe distinguir si avanza 7 u 11 posiciones).

Solución. Definimos de forma recursiva la sucesión \begin{align*} (a_0,b_0,c_0,d_0)&=(a,b,c,d),\\ (a_n,b_n,c_n,d_n)&=(a_{n-1}-b_{n-1},b_{n-1}-c_{n+1},c_{n-1}-d_{n-1},d_{n-1}-a_{n-1}), \end{align*} para todo $n\geq 1$. El problema equivale a comprobar bajo qué condiciones alguno de los números $a_n,b_n,c_n,d_n$ se pasa de $2023$ para algún valor del subíndice $n$ en términos de los valores iniciales. La idea feliz es encontrar la siguiente fórmula válida para todo $n\geq 1$: \[(a_n-c_n)(b_n-d_n)=\begin{cases} (-4)^{\frac{n-1}{2}}[(a-c)^2-(b-d)^2]&\text{si }n\text{ es impar},\\ (-4)^{\frac{n}{2}}[(a-c)(b-d)]&\text{si }n\text{ es par}. \end{cases}\] La probaremos por inducción sobre $n$. Los casos base son $n=1$ y $n=2$, que se comprueban fácilmente. Para $n\geq 3$, se tiene (tras sucesivas simplificaciones) el siguiente desarrollo: \begin{align*} (a_{n}-c_{n})(b_{n}-d_{n})&=(a_{n-1}\!-\!b_{n-1}\!-\!c_{n-1}\!+\!d_{n-1})(b_{n-1}\!-\!c_{n-1}\!-\!d_{n-1}\!+\!a_{n-1})\\ &=(-2b_{n-1}+2d_{n-1})(-2c_{n-1}+2a_{n-1})\\ &=-4(a_{n-1}-c_{n-1})(b_{n-1}-d_{n-1}). \end{align*} Por tanto, por cada dos unidades que avanza el subíndice, aparece un nuevo factor $-4$, lo que se corresponde con la fórmula arriba propuesta (teniendo en cuenta el caso base y la hipótesis de inducción), que queda así probada.

Ahora bien, si $a\neq c$ o bien $b\neq d$, se tiene que $(a-c)(b-d)\neq 0$ o bien $(a-c)^2-(b-d)^2\neq 0$, luego necesariamente $(a_n-c_n)(b_n-d_n)$ se vuelve positivo y arbitrariamente grande en algún momento al ir multiplicado por un factor $(-4)^{n/2}$ o $(-4)^{(n-1)/2}$ (da igual si $(a-c)(b-d)$ o $(a-c)^2-(b-d)^2$ son positivos o negativos porque la potencia tiene base negativa y va tomando alternadamente valores positivos y negativos). Que $(a_n-c_n)(b_n-d_n)$ sea arbitrariamente grande implica claramente que alguno de los números $a_n,b_n,c_n,d_n$ se vuelve arbitrariamente grande.

Finalmente, analizamos qué pasa cuando $a=c$ y $b=d$. No es difícil ver entonces que $a_n=2^{n-1}(a-b)$ y $b_n=2^{n-1}(b-a)$ también por inducción sobre $n$ y dejamos los detalles como ejercicio. Por lo tanto, si $a\neq b$, entonces $a_n$ o $b_n$ se hará mayor que $2023$ en algún momento ya que $2^{n-1}$ se volverá arbitrariamente grande (de nuevo, no importa si $a\gt b$ o $b\gt a$). Con todo esto, deducimos que la única forma de no sobrepasar $2023$ es que $a=b=c=d\lt 2023$, en cuyo caso tenemos obviamente que $a_n=b_n=c_n=d_n=0$ para todo $n\geq 1$.

Solución. Vamos a suponer por comodidad que el cuadrado tiene sus vértices en el plano con coordenadas $(0,0),(1,0),(1,1),(0,1)$ y vamos a parametrizar los distintos casos usando la pendiente $m$ de las rectas paralelas (observamos que, para cada pendiente, hay un único par de rectas que cumple el requisito de la trisección). Aplicando un movimiento rígido podemos suponer además que $0\leq m\leq 1$. Es interesante darse cuenta de que para $m=\frac{2}{3}$ se tiene una trisección especial (figura central) en la que las rectas pasan por vértices del cuadrado. No es difícil calcular en este caso que la distancia entre las dos rectas es $d=\frac{1}{\sqrt{10}}$. Por la simetría de las regiones respecto de la recta de pendiente $m$ que pasa por el centro $(\frac12,\frac12)$, podemos distinguir dos casos:

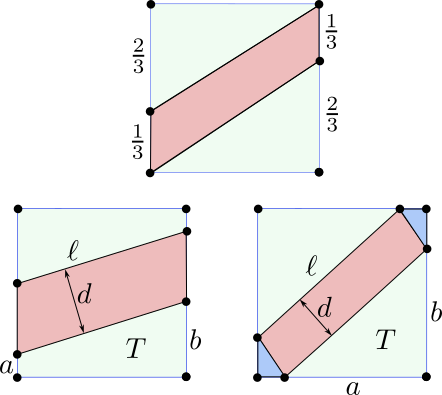
• Caso 1. Las rectas paralelas cortan al cuadrado en lados opuestos. Como la región que delimitan estas rectas es un paralelogramo de base $\ell$ y altura $d$ (según la figura de la izquierda), la condición sobre el área nos dice que $d\cdot\ell=\frac{1}{3}$. Además, si la recta inferior corta a los lados en $(0,a)$ y $(1,b)$ con $b\geq a$, entonces el teorema de Pitágoras nos dice que $\ell^2=1+(b-a)^2$. Además, como el área del trapecio $T$ que queda por debajo de la recta es $\frac{1}{3}$, se tiene que $1\cdot \frac{a+b}{2}=\frac{1}{3}$, o equivalentemente $a+b=\frac{2}{3}$. De todo esto inferimos que \[d=\frac{1}{3\ell}=\frac{1}{3\sqrt{1+(b-a)^2}}=\frac{1}{3\sqrt{1+4(a-\frac{1}{3})^2}}.\] Esto define a $d$ como función de $a$ y además se tiene que $0\leq a\leq\frac{1}{3}$ (si fuera $a\gt\frac{1}{3}$, entonces $b\geq a\geq \frac{1}{3}$ y $T$ contendría un rectángulo de área mayor que $\frac{1}{3}$). En este intervalo la función $1+4(a-\frac{1}{3})^2$ es decreciente, luego $d$ es una función creciente de $a$. El valor mínimo $d=\frac{1}{\sqrt{13}}$ se obtiene para $a=0$ y el máximo $d=\frac{1}{3}$ para $a=\frac{1}{3}$.
• Caso 2. Las rectas paralelas cortan al cuadrado en lados contiguos. Pongamos entonces que la recta inferior corta a los lados en los puntos $(1-a,0)$ y $(0,b)$ con $b\geq a$, lo que define un triángulo $T$ bajo dicha recta. Como el área de $T$ debe ser $\frac{1}{3}$, deducimos que $ab=\frac{2}{3}$. El área de la región entre las dos paralelas está formado por un rectángulo de base $\ell=\sqrt{a^2+b^2}$ y altura $d$ más dos triángulos rectángulos de catetos $1-a$ y $1-b$, lo que nos da un área total $\ell\cdot d+(1-a)(1-b)$. Podemos despejar entonces \begin{align*} d=\frac{\frac{1}{3}-(1-a)(1-b)}{\ell}&=\frac{a+b-\frac{4}{3}}{\sqrt{a^2+b^2}}\\ &=\frac{a+\frac{2}{3a}-\frac{4}{3}}{\sqrt{a^2+\frac{4}{9a^2}}}=\frac{3(a-\frac{2}{3})^2+\frac{2}{3}}{\sqrt{9a^4+4}}. \end{align*} Ahora bien, esto define de nuevo a $d$ como función de $a$ y en este caso $a$ se mueve en el intervalo $[\frac{2}{3},1]$ (si fuera $a\lt \frac{2}{3}$, entonces $T$ estaría contenido en un triángulo de área menor que $\frac{1}{3}$). Para hallar el mínimo de esta función consideramos su derivada, que podemos factorizar como \[d'=\frac{4 \left(9 a^4-9 a^3+6 a-4\right)}{\left(9 a^4+4\right)^{3/2}}=\frac{4(3a^2-2)(3a^2-3a+2)}{\left(9 a^4+4\right)^{3/2}}.\] El factor $3a^2-3a+2$ es siempre positivo y el factor $3a^2-2$ se anula en $a\pm\frac{\sqrt{6}}{3}$. Deducimos que $d$ es decreciente en $[\frac{2}{3},\frac{\sqrt{6}}{3}]$ y creciente en $[\frac{\sqrt{6}}{3},1]$. Por lo tanto, el valor mínimo es $d=\sqrt{2}-\frac{2\sqrt{3}}{3}$, que se obtiene para $a=\frac{\sqrt{6}}{3}$. Para el valor máximo, evaluamos los extremos del intervalo y obtenemos que $d=\frac{1}{\sqrt{13}}$ para $a=\frac{2}{3}$ y también para $a=1$.

Comparando los valores obtenidos, llegamos a que el valor mínimo de la distancia es $\frac{1}{3}$, que se obtiene para dos rectas paralelas a los lados, y que su valor mínimo es $\sqrt{2}-\frac{2\sqrt{3}}{3}$.

Nota. En el problema original, se precisaba no hacer uso de derivadas, lo que requería una dosis de ingenio considerable para cazar el valor $a=\frac{2\sqrt{3}}{3}$ del caso 2. En realidad, la función $d$ en este caso tiene una simetría oculta ya que $d(a)=d(\frac{2}{3a})$. Esto nos asegura que el valor de $a$ tal que $a=\frac{2}{3a}$ debe haber un punto crítico y puede probarse que la función decrece hasta este punto y luego crece. Los detalles puedes encontrarlos en la solución oficial del problema.

Solución. Observemos que $750141=3^7\cdot 7^3$, luego vamos a dividir los $42$ números en $7$ grupos de $3$ y $3$ grupos de $7$. Cada grupo se pone entre paréntesis y luego se añade un signo de multiplicación entre paréntesis consecutivos. De esta forma, el problema se reduce a ver que en cada grupo de $3$ podemos conseguir un múltiplo de $3$ y en cada grupo de $7 un múltiplo de $7$.

• Grupos de 3. Si uno de los tres números es múltiplo de tres, simplemente multiplicamos los tres números. Si los tres números tienen todos resto 1 o todos resto 2 al dividirlos entre tres, sumamos los tres números. Si hay números con resto 1 y números con resto 2 mezclados, simplemente sumamos uno de cada consecutivos, los ponemos entre paréntesis y multiplicamos por el tercero.
• Grupos de 7. Aquí la distinción de casos se vuelve más tediosa (aunque se puede hacer), luego demostraremos de otra forma que hay una cadena consecutiva que suman un múltiplo de 7; bastará sumarla, ponerla entre paréntesis y multiplicar por el resto de números de este grupo. Pongamos que los números son $a_1,a_2,\ldots,a_7$ y vamos haciendo las sumas \begin{align*}&a_1,\\&a_1+a_2,\\ &a_1+a_2+a_3,\\ &\vdots\\ &a_1+a_2+a_3+a_4+a_5+a_6+a_7.\end{align*} Si una de ellas es múltiplo de $7$ habremos terminado; si no, todas dejarán resto entre $1$ y $6$ al dividirlas por $7$. Por el principio del palomar, algún resto se repetirá, luego basta restar la suma de más términos de la suma de menos términos para obtener una subsuma de la forma $a_k+a_{k+1}+\ldots+a_j$ múltiplo de $7$. Por ejemplo, si $a_1+a_2+a_3+a_4+a_5$ y $a_1+a_2$ dejan el mismo resto al dividir por $7$, entonces $a_3+a_4+a_5$ es múltiplo de $7$.

Nota. De la misma forma, se puede probar que en una lista de $n$ números enteros, existe alguna suma de números consecutivos que es múltiplo de $n$.