Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Supongamos que $a\mid b+c$, $b\mid a+c$ y $c\mid a+b$. Si $p$ es un primo que divide a $a$ y $b$, entonces divide a $b+c$ luego también divide a $c$. Este razonamiento nos dice que, si ningún primo divide a los tres, entonces tampoco puede dividir a dos, es decir, $a$, $b$ y $c$ son primos relativos dos a dos. Además, tenemos que $a$, $b$ y $c$ dividen a $a+b+c$, luego $abc$ divide a $a+b+c$ (por ser primos relativos). En partiular, se tiene que $abc\leq a+b+c\leq 3c$, con lo que $ab\leq 3$. Esto nos deja muy pocas posibilidades para el par $(a,b)$:

• Si $a=b=1$, las dos primeras condiciones $a\mid b+c$ y $b\mid a+c$ se cumplen siempre y la tercera $c\mid a+b=2$ nos dice que $c=1$ o $c=2$, luego tenemos las soluciones $(1,1,1)$ y $(1,1,2)$.
• Si $a=1$ y $b=2$, tenemos que $c\mid a+b=3$, luego $c=3$ ya que debe ser $b\geq c$. Se comprueba que $(1,2,3)$ también es solución.
• Si $a=1$ y $b=3$, entonces $c\mid a+b=4$ nos dice que $c=4$ para que sea $b\leq c$, pero no se cumple que $b\mid a+c$, luego no hay soluciones en este caso.

Deducimos así que la terna $(a,b,c)$ es $(1,1,1)$, $(1,1,2)$ o $(1,2,3)$.

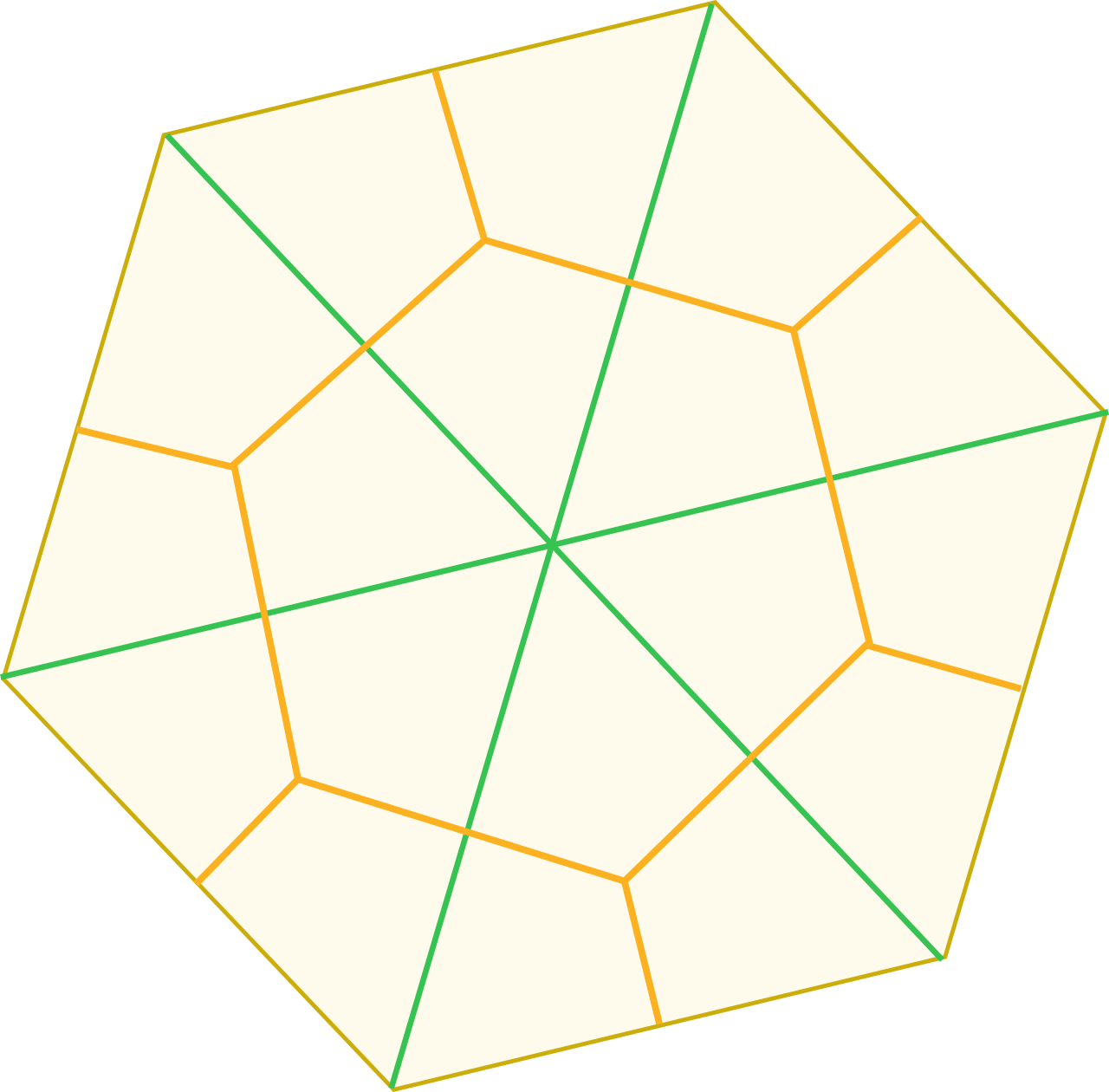
Solución. Consideramos la división del hexágono en 6 triángulos equiláteros de lado 1 indicada con líneas verdes en la figura y luego subdividimos cada triángulo en tres cometas uniendo su centro con los puntos medios de los tres lados, como se ha indicado con línea naranja. Esto nos da un total de 18 regiones y, por el principio del palomar, al menos 2 de los 19 puntos deben caer en una de ellas. Ahora bien, todas las regiones son congruentes entre sí y los puntos más distantes dentro de cada una de ellas son el centro y el vértice del triángulo equilátero en el que está contenida (véase la nota). Dicha distancia máxima es $\frac{2}{3}$ de la altura del triángulo, es decir, $\frac{2}{3}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$.

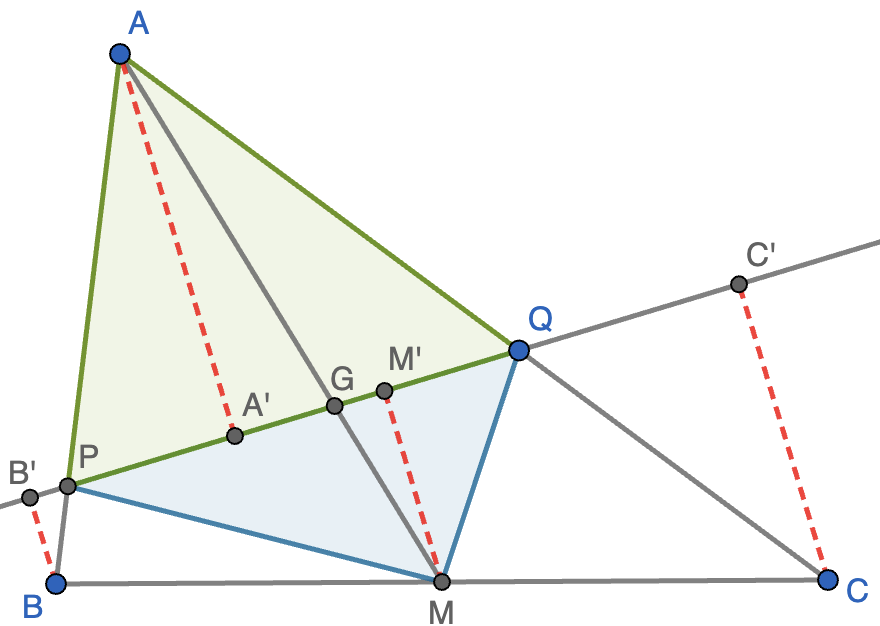
Solución. En primer lugar, nos damos cuenta de que $r$ no es una mediana y deja un vértice a un lado y dos al otro. Supondremos que es el vértice $A$ el que deja a un lado y $B$ y $C$ al otro. Sea $M$ el punto medio de $BC$, $G$ el baricentro y $P$ y $Q$ los puntos de corte de $r$ con los lados $AB$ y $BC$, respectivamente, como se muestra en la figura. También trazamos segmentos perpendiculares a $r$ por $A$, $B$, $C$ y $M$, que tienen sus pies en $A'$, $B'$, $C'$ y $M'$, respectivamente.

Sabemos que el baricentro divide a la mediana $AM$ en dos segmentos tales que $AG=2GM$, luego el triángulo $AGQ$ tiene doble de área del triángulo $GQM$ (tiene la misma altura y base doble) y el triángulo $AGP$ tiene el doble de área que el triángulo $PGM$. Por tanto, el área de $APQ$ (en verde) es también el doble que la de $PQM$ (en azul). Podemos calcular el área de $APQ$ como $\frac{1}{2}AA'\cdot PQ$ y el área de $PQM$ como $\frac{1}{2}MM'\cdot PQ$. Ahora nos damos cuenta de que $MM'=\frac{1}{2}(BB'+CC')$ por el teorema de Thales ya que $BB',MM',CC'$ son paralelas que cortan a $r$ y $BC$ con $BM=CM$. Por lo tanto, el área de $PQM$ es $\frac{1}{4}(BB'+CC')PQ$, que debe ser la mitad de $\frac{1}{2}AA'\cdot PQ$, luego necesariamente $AA'=BB'+CC'$, que es lo que queríamos demostrar.

Solución. Vamos a trabajar en coordenadas, escribiendo los vértices del triángulo como $(x_1,y_1)$, $(x_2,y_2)$ y $(x_3,y_3)$. Las coordenadas del baricentro son la media aritmética, es decir, \[\left(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3}\right).\] Por tanto, una recta que pasa por este punto tendrá ecuación $Ax+By+C=0$, siendo $A,B,C\in\mathbb{R}$ tales que $A^2+B^2\neq 0$ y \[A\frac{x_1+x_2+x_3}{3}+B\frac{y_1+y_2+y_3}{3}+C=0.\] Esto último puede reescribirse como \[\frac{Ax_1+By_1+C}{3}+\frac{Ax_2+By_2+C}{3}+\frac{Ax_3+By_3+C}{3}=0.\] Como las tres fracciones suman cero, habrá dos de ellas con un signo y otra con el signo opuesto (no pueden ser cero porque la recta no pasa por ningún vértice). Supondremos que las dos primeras son del mismo signo y la tercera del signo opuesto, luego tomando valores absolutos, dividiendo por $\sqrt{A^2+B^2}$ y multiplicando por $3$, tenemos \[\frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}}+\frac{|Ax_2+By_2+C|}{\sqrt{A^2+B^2}}=\frac{|Ax_3+By_3+C|}{\sqrt{A^2+B^2}}.\] Cada fracción es la distancia desde el vértice correspondiente a la recta, luego el resultado está probado. El hecho de que dos fracciones tengan el mismo signo y otra el signo opuesto refleja el hecho de que la recta deja a dos puntos a un lado y al tercero al otro.