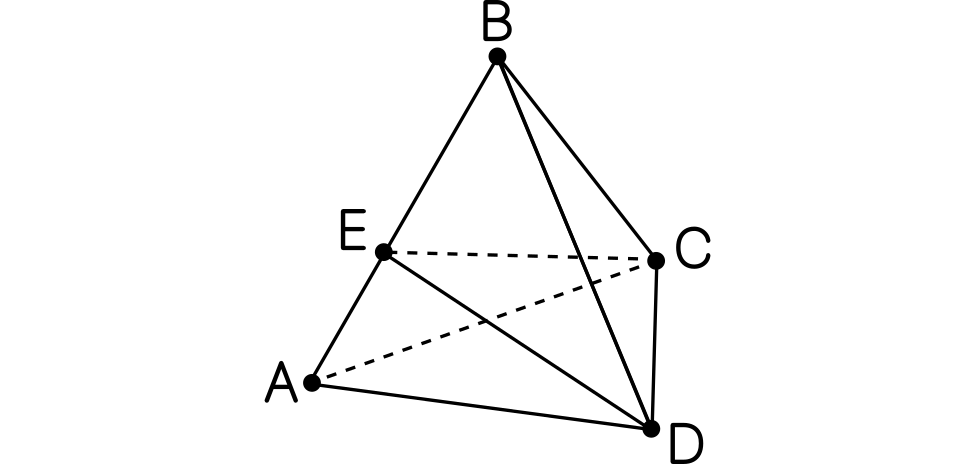
Se considera un tetraedro regular como el de la figura. Si el punto $E$ recorre la arista $AB$. ¿Cuándo el ángulo $\angle CED$ es máximo?
pistasolución 1info
Pista. Si $M$ es el punto medio de $CD$, demuestra el ángulo será máximo cuando la longitud de $EM$ sea mínima.
Solución. Sea $M$ el punto medio de $CD$, de forma que $EM$ es una altura del triángulo isósceles $CDE$. El ángulo $\alpha=\angle CED$ verifica que $\mathrm{tan}(\frac{\alpha}{2})=\frac{CM}{EM}$. El ángulo será máximo cuando la tangente sea máxima, es decir, cuando $EM$ sea mínimo ya que $CM$ no depende de dónde hayamos puesto el punto $E$. Ahora podemos restringirnos al plano que contiene al triángulo $ABM$. El segmento $EM$ está en este plano y su longitud será mínima cuando $EM$ sea perpendicular a $AB$, es decir, cuando $EM$ sea una altura de $ABM$, que coincide con la mediatriz por ser $ABM$ isósceles. Concluimos que el ángulo $\angle CED$ es máximo cuando $E$ es el punto medio de $AB$.
Nota. Usando el seno en lugar de la tangente, también puede razonarse de forma similar que lo que hay que minimizar es la longitud de $CE$, lo que nos lleva a que ha de ser perpendicular a $AC$ y $E$ tiene que ser el punto medio.
Dado el polinomio $P(x)=x^4+\square x^3 +\square x^2 +\square x + \square$, en el que cada cuadrado representa un hueco donde se colocará un coeficiente, se plantea el siguiente juego entre dos jugadores: Alternativamente, el primer y el segundo jugador eligen un hueco vacío y colocan en él un entero no nulo hasta rellenar los cuatro huecos. Si el polinomio resultante tiene al menos dos raíces enteras gana el segundo jugador; en otro caso, el ganador es el primero. Demostrar que, eligiendo la estrategia adecuada, el primer jugador siempre puede ganar.
pistasolución 1info
Pista. Poner $1$ o $-1$ en el término independiente limita considerablemente las posibles raíces enteras.
Solución. El primer jugador comienza poniendo un $-1$ en el término independiente, de forma que se limitan las posibles soluciones enteras a $1$ y $-1$. Consideremos las posibles factorizaciones:
\begin{align*}
(x-1)(x+1)(x^2+ax+1)&=x^4+ax^3-ax-1,\\
(x+1)^2(x^2+ax+1)&=x^4+(a+2)x^3+2ax^2+(a-2)x-1,\\
(x-1)^2(x^2+ax+1)&=x^4+(a-2)x^3-2ax^2+(a+2)x-1.\\
\end{align*}
La primera factorización no es posible ya que implica poner un $0$ en el término de grado $2$. Ahora, cuando el segundo jugador pone un número en uno de los coeficientes de $x$, $x^2$ o $x^3$, determinar a lo sumo dos valores de $a$ (uno para la segunda factorización y otro para la tercera). El primer jugador sólo tiene que escribir en uno de los huecos restantes un número que determine un valor de $a$ diferente de estos dos.
Nota. Si el primer jugador pone un $1$ en lugar de $-1$ en el término independiente, entonces es el segundo jugador el que tiene la estrategia ganadora. Para verlo, tomamos la factorización
\[(x-1)(x+1)(x^2+ax-1)=x^4+ax^3-2x^2-ax+1.\]
Si el segundo juega un $-2$ en el término de $x^2$, en su segundo turno solo tendrá que poner lo opuesto a lo que haya puesto el primer jugador en su segundo turno.
Calcula las soluciones reales de la ecuación
\[\sqrt[4]{97-x}+\sqrt[4]{x}=5.\]
pistasolución 1info
Pista. Plantea un sistema con las incógnitas $a=\sqrt[4]{97-x}$ y $b=\sqrt[4]{x}$.
Solución. Llamamos $a=\sqrt[4]{97-x}$ y $b=\sqrt[4]{x}$, con lo que la ecuación que nos dan se puede escribir de forma equivalente como el siguiente sistema:
\[\left\{\begin{array}{l}a+b=5\\a^4+b^4=97\end{array}\right.\]
Utilizando el binomio de Newton, podemos desarrollar
\begin{align*}
(a+b)^4&=a^4+4a^3b+6a^2b^2+4ab^3+b^4\\
&=a^4+b^4+4ab(a^2+b^2)+6a^2b^2\\
&=a^4+b^4+4ab((a+b)^2-2ab)+6a^2b^2\\
&=a^4+b^4+4ab(a+b)^2-2a^2b^2.
\end{align*}
Sustituyendo $a+b=5$ y $a^4+b^4=97$, obtenemos la siguiente ecuación de segundo grado en la incógnita $ab$, que podemos resolver fácilmente:
\[(ab)^2-50ab+264=0\ \Longrightarrow\ ab=\frac{50\pm \sqrt{1444}}{2}=\begin{cases}44,\\6.\end{cases}\]
Distinguimos dos casos:
- Si $ab=44$, entonces tenemos la suma $a+b=5$ y el producto $ab=44$, lugo podemos despejar $a$ y $b$ como las soluciones de la ecuación de segundo grado $x^2-5x+44=0$. Esta ecuación no tiene soluciones reales.
- Si $ab=6$, entonces $a$ y $b$ son las soluciones de la ecuación de segundo grado $x^2-5x+6=0$, es decir, $(a,b)=(2,3)$ o bien $(a,b)=(3,2)$. Como $x=b^4$, tenemos las soluciones $x=16$ y $x=81$, que claramente verifican la ecuación inicial.
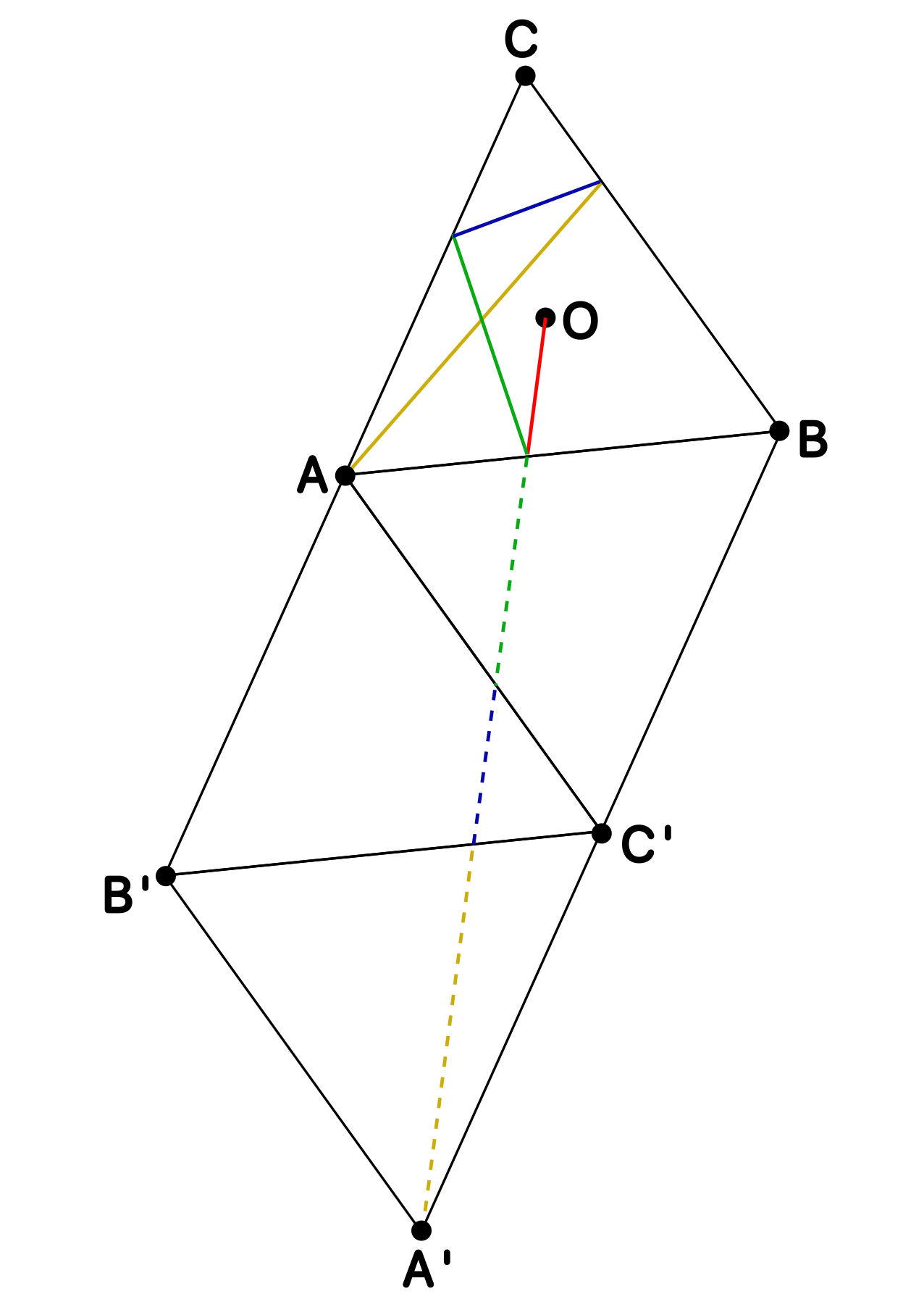
Se considera un triángulo equilátero de lado $1$ y centro $O$, como el de la figura. Un rayo parte de $O$ y se refleja tres veces: primero en el lado $AB$, después en el lado $AC$ y finalmente en el lado $BC$. El rayo termina alcanzando el vértice $A$. Determinar la longitud mínima de un rayo en tales condiciones.
Nota. Cuando un rayo se refleja en un lado, los ángulos de entrada (incidencia) y salida (reflexión) coinciden.

pistasolución 1info
Pista. Refleja el triángulo $ABC$ respecto de sus lados.
Solución. Si reflejamos repetidamente el triángulo respecto de sus lados, entonces la poligonal que forma la trayectoria del rayo se vuelve una línea recta ya que el ángulo de incidencia es el de reflexión. Como nos dicen que se refleja primero respecto de $AB$, luego $AC$ y por último $BC$, estas son las reflexiones que debemos hacer y que hemos dibujado en la figura. Vemos así que hay una única forma hacer los rebotes para que se cumpla la condición del enunciado y ahora solamente hay que calcular su longitud.
Para ello, observamos que $OBA'$ es un triángulo rectángulo ya que $OB$ es una altura del triángulo equilátero y $BA'$ es paralela al lado opuesto. Además, se tiene que $OB=\frac{2}{3}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$ (dos tercios de la altura) y $BA'=2$ (dos veces el lado), luego el teorema de Pitágoras nos da la distancia que buscamos:
\[OA'=\sqrt{\left(\tfrac{\sqrt{3}}{3}\right)^2+2^2}=\frac{\sqrt{39}}{3}.\]