Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Nota. La desigualdad de Jensen nos dice que si $f(x)$ es una función cóncava en un intervalo $[a,b]$ y tenemos puntos $x_1,\ldots,x_n\in [a,b]$ y pesos $w_1,\ldots,w_n\gt 0$, entonces \[\frac{w_1f(x_1)+w_2f(x_2)+\ldots+w_nf(x_n)}{w_1+w_2+\ldots+w_n}\leq f(\frac{w_1x_1+w_2x_2+\ldots+w_nx_n}{w_1+w_2+\ldots+w_n}).\]
Informar de error en enunciado Informar de procedencia del problema
Nota. Por ejemplo, si $n=1$, la respuesta es cualquier número natural
ya que podemos dar la vuelta a cuantos cuadrados $1\times 1$ deseemos.
Informar de error en enunciado Informar de procedencia del problema
Para ver qué ocurre con $0224$, pongamos $n=100a+10b+c$, con $0\leq a,b,c\leq 9$ respectivamente. Podemos hacer la multiplicación siguiente: \[\begin{array}{ccccc} &&a&b&c\\ &\times&a&b&c\\\hline &&ac&bc&c^2\\ &ab&b^2&bc&\\ a^2&ab&ac&&\\\hline a^2&2ab&b^2\!+\!2ac&2bc&c^2 \end{array}\] y ahora ir cuadrando las cifras desde las unidades a las centenas. Esto es bastante rutinario, pero hay que tener cuidado de tener en cuenta las llevadas (no se han escrito en la multiplicación anterior ya que dependen de los valores concretos de $a,b,c$). En las unidades tenemos que $c^2\equiv 4\ (\text{mód } 10)$, con soluciones $c=2$ y $c=8$.
- Si $c=2$, entonces en las decenas tenemos que $6b\equiv 2\ (\text{mód }10)$, que tiene soluciones $b=3$ y $b=8$. Para que $10b+c$ sea múltiplo de $4$, tiene que ser $b=3$, luego las centenas cuadran cuando $4a\equiv 2\ (\text{mód }10)$, que tiene soluciones $a=3$ y $a=8$. Tenemos que $332^2=110224$ sí cumple la condición pero $832^2=692224$ no.
- Si $c=8$, entonces $6b\equiv 6\ (\text{mód }10)$, que tiene soluciones $b=1$ y $b=6$. Para que $10b+c$ sea múltiplo de $4$, tiene que ser $b=6$. Cuandrando las centenas, tenemos que $6a\equiv 6\ (\text{mód }10)$, que tiene soluciones $a=1$ y $a=6$. Sin embargo, las unidades de millar de $168^2=28224$ ni $668^2=446224$ no cuadran.
Informar de error en enunciado Informar de procedencia del problema
Nota. No se puede expresar el resultado final en términos de funciones trigonométricas.
En el pentágono regular de lado $1$ de la figura, los triángulos $ACD$ y $DEP$ son semejantes pues sus lados son paralelos. Si llamamos $d$ a la longitud de la diagonal del pentágono, la semejanza $\frac{AD}{CD}=\frac{DE}{PE}$ se escribe como $\frac{d}{1}=\frac{1}{d-1}$, de donde $d$ cumple la ecuación $d^2-d-1=0$, de la que nos quedamos con la única solución positiva $d=\frac{1+\sqrt{5}}{2}$, la razón áurea. Ahora bien, el triángulo $ABQ$ de la figura es rectángulo y cumple $\angle BAQ=54$, luego \begin{align*}
\mathrm{sen}(54)&=BD=\frac{d}{2}=\frac{1+\sqrt{5}}{4},\\
\cos(54)&=AQ=\sqrt{1-BQ^2}=\sqrt{1-\left(\tfrac{1+\sqrt{5}}{4}\right)^2}=\frac{\sqrt{5-\sqrt{5}}}{2\sqrt{2}}.
\end{align*}
De esta forma, tenemos que el área del triángulo es
\[8\,\mathrm{sen}(54)\cos(54)=8\frac{1+\sqrt{5}}{4}\cdot\frac{\sqrt{5-\sqrt{5}}}{2\sqrt{2}}=\sqrt{10+2\sqrt{5}}.\]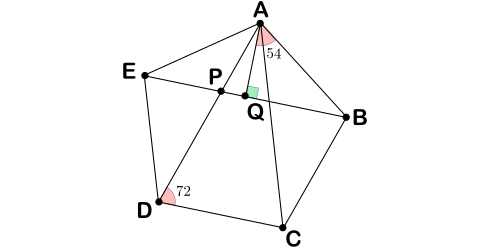
Informar de error en enunciado Informar de procedencia del problema
El área del triángulo $AOB$ se puede calcular de dos maneras equivalentes: \[\tfrac{1}{2}AB\cdot OP=\mathrm{Area}(AOB)=\tfrac{1}{2}BO\cdot AO\,\mathrm{sen}(60^\circ)=\tfrac{\sqrt{3}}{4}BO\cdot AO.\] Multiplicando por $(1+\lambda)$ y usando que \begin{align*} AC&=AO+OC=(1+\lambda)AO=7,\\ PQ&=OP+OQ=(1+\lambda)OP=4\sqrt{3}, \end{align*} según la información del enunciado, la igualdad de áreas se puede reescribir como \[AB\cdot (1+\lambda)OP=\tfrac{\sqrt{3}}{2}BO\cdot (1+\lambda)AO\ \Leftrightarrow\ \frac{BO}{AB}=\frac{8}{7}.\] Ahora bien, el teorema del coseno aplicado al triángulo $AOB$ nos dice que \[AB^2=BO^2+AO^2-2BO\cdot AO\cos(60^\circ)=BO^2+AO^2-BO\cdot AO,\] Dividiendo por $AB^2$, esto puede reescribirse como \[1=\left(\frac{BO}{AB}\right)^2+\left(\frac{AO}{AB}\right)^2-\frac{BO}{AB}\cdot \frac{AO}{AB}.\] Sustituyendo $\frac{BO}{AB}=\frac{8}{7}$ nos queda una ecuación de segundo grado en la incógnita $\frac{AO}{AB}$, que se resuelve fácilmente dando dos soluciones positivas: $\frac{AO}{AB}=\frac{3}{7}$ y $\frac{AO}{AB}=\frac{5}{7}$. Teniendo en cuenta que $AO=\frac{7}{1+\lambda}$, las soluciones anteriores nos dan $(1+\lambda)AB=\frac{49}{3}$ o bien $(1+\lambda)AB=\frac{49}{5}$.
Finalmente, como el área del trapecio está dada por $S=\frac{1}{2}(AB+CD)PQ=\frac{1}{2}(1+\lambda)AB\cdot PQ$ y que $PQ=4\sqrt{3}$ es conocido, llegamos a que las posibles soluciones son \[S=\frac{98\sqrt{3}}{3}\quad\text{y}\quad S=\frac{98\sqrt{3}}{5}.\] Las dos soluciones se corresponden con que $C$ se proyecte sobre $AB$.

Informar de error en enunciado Informar de procedencia del problema