Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Si aplicamos la desigualdad de Cauchy-Schwarz a los vectores \[u=\left(\sqrt{3^x},\sqrt{5^y},\sqrt{7^z}\right),\qquad v=\left(\sqrt{5^y+7^z},\sqrt{3^x+7^z},\sqrt{3^x+5^y}\right),\] obtenemos que \begin{align*} \sqrt{3^x(5^y+7^z)}+\sqrt{5^y(7^z+3^x)}+\sqrt{7^z(3^x+5^y)}&\leq\sqrt{3^x+5^y+7^z}\sqrt{(5^y+7^z)+(3^x+7^z)+(3^x+5^y)}\\ &=\sqrt{2}(3^x+5^y+7^z), \end{align*} donde hemos usado también que las exponenciales $3^x,5^7,7^z$ son números positivos. Esto nos dice que las soluciones de la ecuación son precisamente los valores que hacen de la desigualdad de Cauchy-Schwarz una igualdad. Esto equivale a que los vectores $u$ y $v$ sean proporcionales. Como están formados por números positivos, estamos buscando los $x,y,z$ tales que existe $\lambda\gt 0$ tal que \[\sqrt{3^x}=\lambda\sqrt{5^y+7^z},\qquad \sqrt{5^y}=\lambda\sqrt{3^x+7^z},\qquad \sqrt{7^z}=\lambda\sqrt{3^x+5^y}.\] Elevando al cuadrado y sumando los resultados, llegamos a que $3^x+5^y+7^z=2\lambda^2(3^x+5^y+7^z)$, luego debe ser $\lambda=\frac{1}{\sqrt{2}}$ ya que podemos cancelar $3^x+5^y+7^z\neq 0$ (recordemos que $\lambda$ es positivo). Por lo tanto, el sistema anterior nos queda \[3^x=\frac{5^y+7^z}{2},\qquad 5^y=\frac{3^x+7^z}{2},\qquad 7^z=\frac{3^x+5^y}{2}.\] Este es un sistema lineal en las incógnitas $3^x,5^y,7^z$, que es compatible indeterminado y sus soluciones son los números que verifican $3^x=5^y=7^z$. Tomando logaritmos, podemos reescribir esto como $x\log(3)=y\log(5)=z\log(7)$, luego las soluciones que buscamos pueden parametrizarse en términos de un parámetro real $a\in\mathbb{R}$ como \[(x,y,z)=\left(\frac{a}{\log(3)},\frac{a}{\log(5)},\frac{a}{\log(7)}\right).\]

Solución. Un miembro concreto $A$ sólo puede estar en $6$ comités como máximo ya que hay otras $24$ personas y no puede haber dos de ellas en el mismo comité en que está también $A$. Esto nos dice que, al mirar el club al completo, hay como máximo $6\cdot 25=150$ pertenencias, pero esto nos da $150:5=30$ comités ya que cada uno lo estamos contando $5$ veces (una por cada uno de sus miembros).

Nota. Una pregunta natural es si $30$ es el número óptimo y la respuesta es que sí. Se pueden encontrar formas de distribuir los $30$ comités de $5$ miembros con un solo miembro en la intersección de cada para de ellos. Una forma muy interesante de hacerlo es tomar cada miembro del club como uno puntos $(x,y)$ de coordenadas enteras entre $0$ y $4$ (un total de $25$ puntos). Cada comité estaría formado por los puntos que cumplen la condición $ax+by\equiv c\ (\text{mod }5)$, siendo $a,b\in\mathbb{Z}$ números enteros. ¿Sabrías probar que hay exactamente $30$ comités y dos cualesquiera de ellos tienen $0$ o $1$ elementos en común?

Solución. Sea $ABC$ el triángulo en cuestión y supongamos que el ángulo en $A$ está fijo y también el radio $r$ de la circunferencia inscrita, que es tangente a los lados en los puntos $X,Y,Z$, como se muestra en la figura. El área del triángulo está dada por $S=rp$, siendo $p$ el semiperímetro, luego minimizar el perímetro del triángulo equivale a minimizar su área cuando variamos $X$ en el arco mayor $YZ$. Es fácil intuir que la solución al problema es el triángulo isósceles $ARS$ tangente a la circunferencia inscrita en el punto medio $M$ de $RS$. Vamos a confirmar esta intuición viendo que cualquier otra elección de $X$ distinta de $M$ nos da un triángulo $ABC$ de área mayor que $ARS$. Si suponemos sin perder generalidad que $X$ está en el arco $MZ$ (en caso de estar en $MY$ el razonamiento es similar), probaremos que el área de $PBR$ (en verde) es menor que el área de $PCS$ (en azul), siendo $P$ el punto en de corte entre $BC$ y $RS$.

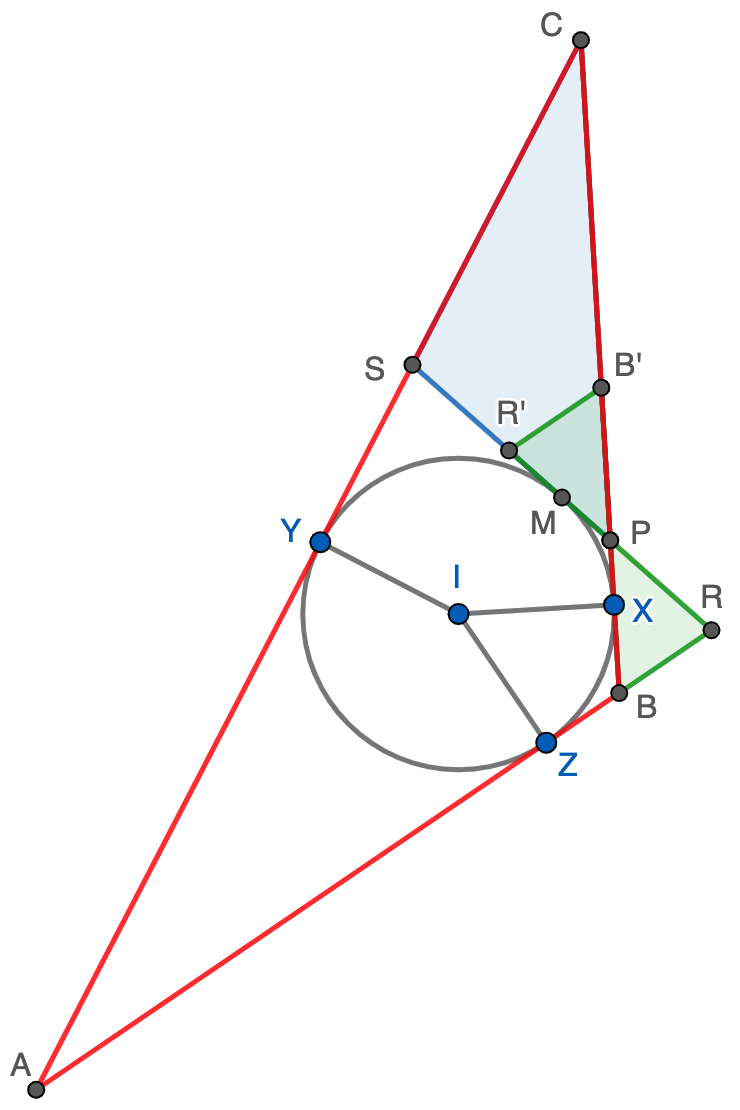
Como $P$ está en el segmento $MR$ y $M$ es el punto medio de $RS$, se sigue que $PR\lt PS$; además, se tiene que $\angle PRB$ es agudo mientras que $\angle CSR=180-\angle PRB$ es obtuso. Esto nos dice que si giramos $180^\circ$ el triángulo $PRB$ respecto de $P$ obtenemos un triángulo $PR'B'$ contenido en $PCS$, luego ciertamente el área de $PBR$ es menor que el área de $PCS$ y hemos terminado la demostración.

Solución. Los enteros a considerar son de la forma $2^a\cdot 3^b\cdot 5^c\cdot 7^d$. Hay $16=2^4$ posibilidades para la paridad de los cuatro exponentes ya que cada uno de ellos puede ser par o impar. Como tenemos 17 números de esta forma, al menos dos de ellos tendrán cada uno de los cuatro exponentes con la misma paridad. Al multiplicarlos, como se suman los exponentes, obtenemos otro número de la misma forma con todos los exponentes pares, es decir, un cuadrado perfecto.