Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Sea $ABCD$ el cuadrilátero convexo y $P$ el punto de corte de las diagonales. Si llamamos $S_1,S_2,S_3,S_4$ a las áreas de los cuatro triángulos en que las diagonales dividen al cuadrilátero, como se indica en la figura, entonces la propiedad de la bisección nos dice que \[S_1+S_2=S2+S_3=S_3+S_4=S_4+S_1\ \Longleftrightarrow\ \begin{cases}S_1=S_3,\\S_2=S_4.\end{cases}\] Ahora bien, para que la diagonal $BD$ biseque, las distancias de $A$ y $C$ a la recta $BD$ deben ser las mismas (las alturas de los triángulos $ABD$ y $BCD$ de base común $BD$, indicadas con línea discontinua roja). Por lo tanto, tiene que ser $BP=DP$ para que se cumpla que $S_1=S_3$. Análogamente, se demuestra que $AP=CP$, luego hemos llegado a que las diagonales se cortan en su punto medio y esto implica que $ABCD$ es un paralelogramo.

Solución. El polinomio $x^5+x+1$ no tiene raíces enteras pero puede factorizarse como producto de un polinomio de grado $3$ por otro de grado $2$. Para ello, pongamos \begin{align*} x^5+x+1&=(x^3+ax^2+bx+c)(x^2+ex+f)\\ &=x^5+(a+e)x^4+(b+ae+f)x^3+(c+be+af)x^2+(ce+bf)x+cf. \end{align*} Igualando coeficientes, tenemos en primer lugar que $cf=1$, luego pondremos $c=f=1$ ya que buscamos coeficientes enteros (si no nos sale, deberíamos probar con la otra opción $c=f=-1$). Entonces, nos queda que $a+e=0$, $b+ae=-1$, $a+be=-1$ y $e+b=1$. Podemos sustituir entonces $a=-e$ y $b=1-e$ en $b+ae=-1$ para llegar a que $1-e-e^2=-1$, ecuación que tiene soluciones $e=1$ y $e=-2$. Con $e=1$, tenemos $a=-1$ y $b=0$, que cumplen la ecuación restante ($a+be=-1$) y nos dan la factorización deseada: \[x^5+x+1=(x^3-x^2+1)(x^2+x+1).\] Esto nos dice que el número original se puede factorizar (con $x=2^m$) como \[2^{5m}+2^m+1=(2^{3m}-2^{2m}+1)(2^{2m}+2^{m}+1).\] Está claro que $2^{3m}-2^{2m}\gt 0$ (puesto que $m\gt 0$), luego el primer factor no es $\pm 1$. Tampoco lo es el segundo (ya que es mayor que $1$), luego el número $2^{5m}+2^m+1$ es compuesto para todo entero $m\geq 1$.

Solución. La desigualdad se puede escribir de forma equivalente como \[\left(\frac{1}{a}\right)^{a^2+2ac}\left(\frac{1}{b}\right)^{b^2+2ab}\left(\frac{1}{c}\right)^{c^2+2bc}\leq 3.\] La desigualdad entre las medias aritmética y geométrica con pesos nos dice que si $x_1,x_2,x_3,w_1,w_2,w_3\geq 0$ son tales que $w_1+w_2+w_3=1$, entonces $x_1^{w_1}x_2^{w_2}x_3^{w_3}\leq w_1x_1+w_2x_2+w_3x_3$. En nuestro caso, tomaremos $x_1=\frac{1}{a}$, $x_2=\frac{1}{b}$, $x_3=\frac{1}{c}$, $w_1=a^2+2ca$, $w_2=b^2+2ab$ y $w_3^2=c^2+2bc$, que claramente verifican $w_1+w_2+w_3=(a+b+c)^2=1$. Tenemos entonces que \begin{align*} \left(\frac{1}{a}\right)^{a^2+2ac}\left(\frac{1}{b}\right)^{b^2+2ab}\left(\frac{1}{c}\right)^{c^2+2bc}&\leq \frac{a^2+2ca}{a}+\frac{b^2+2ab}{b}+\frac{c^2+2bc}{c}\\ &=3(a+b+c)=3. \end{align*}

Nota. La desigualdad entre las medias aritmética y geométrica con pesos se puede ver también como la desigualdad de Jensen para la función cóncava $f(t)=\ln(t)$. La pista la da el hecho de que los exponentes sumen $1$ pero puede ser difícil darse cuenta de que hay que invertir primero para que los signos de la desigualdad vayan en el sentido correcto.

Como los pesos son todos positivos, la igualdad se alcanza sólo cuando $x_1=x_2=x_3$, es decir, cuando $a=b=c$.

Solución. Sea $\Gamma$ la circunferencia que nos dan, con centro $O$ y radio $R$. El problema es equivalente a encontrar un punto $X\in\Gamma$ tal que $PQX$ sea un triángulo rectángulo con ángulo recto en $X$ pues que en tal caso bastaría prolongar los lados $PX$ y $QX$ hasta que corten en sendos puntos $Y$ y $Z$ a la circunferencia (distintos de $X$), de forma que $XYZ$ es el triángulo inscrito que buscamos. El lugar geométrico de los puntos $X$ tales que $PQX$ es rectángulo con ángulo recto en $X$ es la circunferencia de diámetro $PQ$, luego existirá el punto que buscamos si y solo si la circunferencia de diámetro $PQ$ corta a $\Gamma$ Como la circunferencia de diámetro $PQ$ tiene centro en $M$, el punto medio de $PQ$, el problema tiene solución si y solo si $OM+MP\geq R$ (observemos que $OM+MP$ es la distancia más alejada de $O$ que se puede alcanzar con la circunferencia de diámetro $PQ$).

Para terminar, vamos a expresar el resultado sin que intervenga $M$, por rizar el rizo. Tenemos que $MP=\frac{1}{2}PQ$ y que $OM$ es la mediana de $OPQ$. Usando la fórmula de la meidana, la condición que buscamos se puede escribir finalmente como \[\frac{1}{2}PQ+\sqrt{\frac{OP^2+OQ^2}{2}-\frac{PQ^2}{4}}\geq R.\]

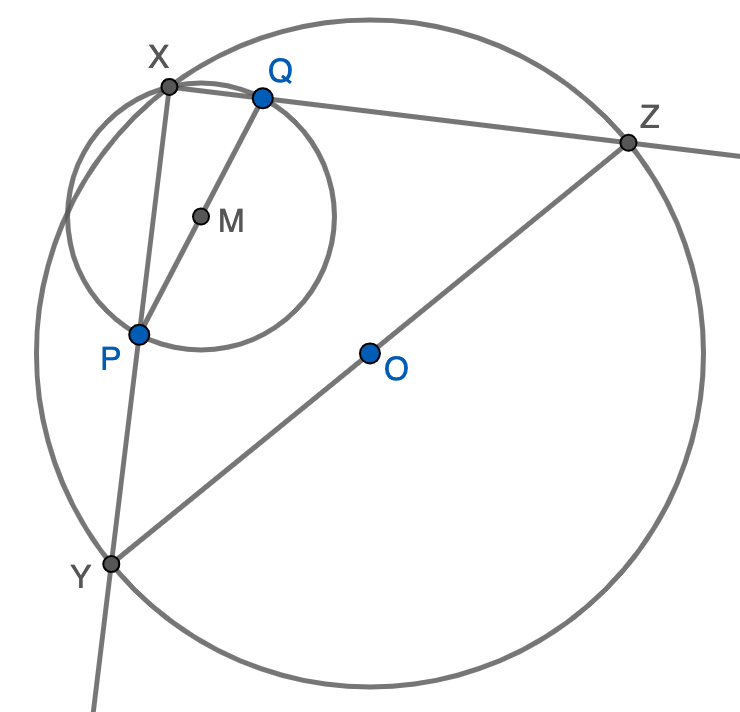
Nota. En realidad, cuando la desigualdad es estricta, hay dos soluciones ya que hay dos puntos de corte de ambas circunferencias.

Solución. Comencemos con el segundo sumando. Como $2222\equiv 3\ (\text{mod }7)$, tenemos que $2222^{5555}\equiv 3^{5555}\ (\text{mod }7)$. Ahora bien, para simplificar el exponente que, trabajando módulo $7$, tenemos que $3^1\equiv 3$, $3^2\equiv 2$, $3^3\equiv 6$, $3^4\equiv 4$, $3^5\equiv 5$ y $3^6\equiv 1$. Hemos llegado a una potencia que es congruente con $1$. Ahora si dividimos $5555$ entre $6$ obtenemos que $5555=925\cdot 6+5$, luego \[2222^{5555}\equiv 3^{5555}=(3^6)^{925}\cdot 3^5\equiv 1^{925}\cdot 5\equiv 5\ (\text{mod }7).\]

De la misma manera, se comprueba que $5555\equiv 4\ (\text{mod }7)$, luego $5555^{222}\equiv 4^{2222}\ (\text{mod }7)$. Tenemos que $4^1\equiv 4$, $4^2\equiv 2$ y $4^3\equiv 1$ módulo $7$, y hacemos la división euclídea de $2222$ entre $3$, que nos da $2222=740\cdot 3+2$. Por tanto, \[5555^{2222}\equiv 4^{2222}=(4^3)^{740}\cdot 4^2\equiv 1^{740}\cdot 2\equiv 2\ (\text{mod }7).\] Esto nos da finalmente el resultado deseado: \[2222^{5555}+5555^{2222}\equiv 5+2\equiv 0\ (\text{mod }7).\]