Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 814
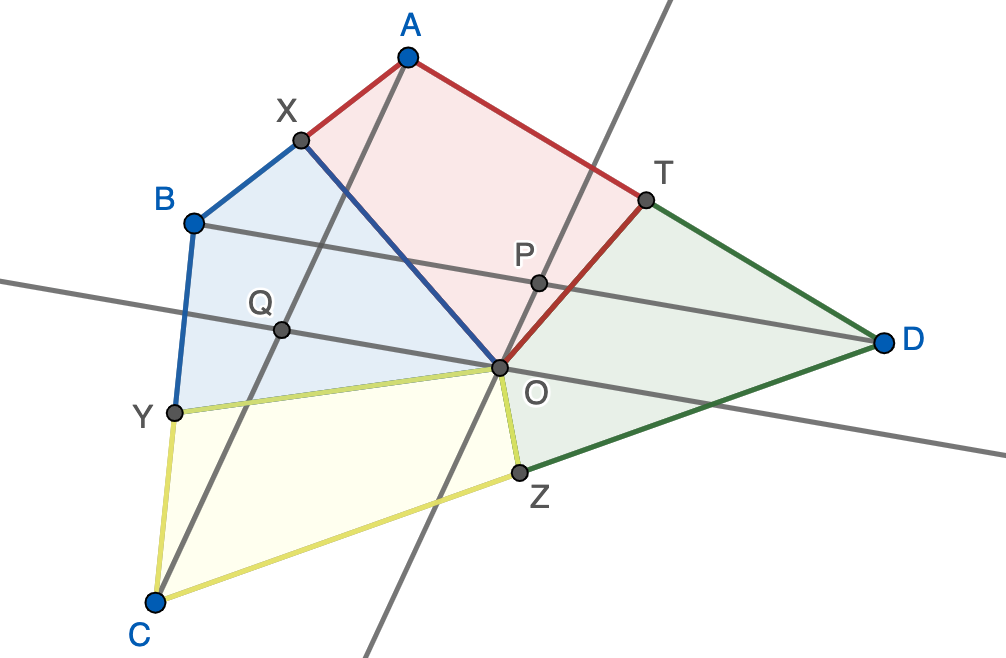
Sea $ABCD$ un cuadrilátero cualquiera. Sean $P$ y $Q$ los puntos medios de las diagonales $BD$ y $AC$, respectivamente. Las paralelas por $P$ y $Q$ a la otra diagonal se cortan en $O$. Si unimos $O$ con las cuatro puntos medios de los lados $X$, $Y$, $Z$ y $T$ se forman cuatro cuadriláteros: $OXBY$, $OYCZ$, $OZDT$ y $OTAX$. Probar que los cuatro cuadriláteros tienen la misma área.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 813
Tenemos un conjunto de $221$ números reales cuya suma es $110721$. Los disponemos formando una tabla rectangular de modo que todas las filas y la primera y última columnas son progresiones aritméticas de más de un elemento. Probar que la suma de los elementos de las cuatro esquinas vale $2004$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 812
Probar que para cualquier primo $p$ distinto de $2$ y $5$ existe un múltiplo de $p$ cuyas cifras son todas nueves. Por ejemplo, si $p = 13$, tenemos que $999999=13\cdot 76923$.
pistasolución 1info
Pista. Utiliza el teorema pequeño de Fermat
Solución. Si $p$ es un número primo distinto de $2$ y $5$, entonces es primo relativo con $10$, luego el teorema pequeño de Fermat nos asegura que $10^{p-1}\equiv 1\ (\text{mod }p)$. En otras palabras, el número $10^{p-1}-1$, que se escribe solo con nueves, es múltiplo de $p$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 811
Se consideran $2002$ segmentos en el plano tales que la suma de sus longitudes es la unidad. Probar que existe una recta $r$ tal que la suma de las longitudes de las proyecciones de los $2002$ segmentos dados sobre $r$ es menor que $\frac{2}{3}$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 810
Sea $n$ un número natural y $m$ el que resulta al escribir en orden inverso las cifras de $n$. Determinar, si existen, los números de tres cifras que cumplen $2m+S=n$, siendo $S$ la suma de las cifras de $n$.
pistasolución 1info
Pista. Escribe la condición como una ecuación con tres incógnitas, los dígitos de $n$. Estudia dicha ecuación módulo distintos números para obtener información.
Solución. Sean $a,b,c$ las cifras de las centenas, decenas y unidades del número $n$, respectivamente. Por lo tanto, podemos escribir
\[\left\{\ \begin{array}{l}
n=100a+10b+c\\
m=100c+10b+a\\
S=a+b+c
\end{array}\right.\]
De esta forma, podemos escribir la condición que nos dan como
\[0=n-2m-S=97a-11b-200c.\]
Si miramos esta ecuación módulo $2$, $9$ y $11$, obtenemos
\begin{align*}
0&=97a-11b-200c\equiv a-b\ (\text{mod }2),\\
0&=97a-11b-200c\equiv 2(a+b+c)\ (\text{mod }9),\\
0&=97a-11b-200c\equiv -2(a+c)\ (\text{mod }11).&
\end{align*}
Deducimos que $a$ y $b$ tienen la misma paridad, que $a+b+c$ es múltiplo de $9$ y que $a+c$ es múltiplo de $11$. Como $1\leq a\leq 9$ y $0\leq c\leq 9$, esta última condición nos dice que $a+c=11$ y tenemos solo 8 posibilidades para el par $(a,c)$. Por otro lado, $11+b=a+b+c\equiv 0\ (\text{mod }9)$, nos da necesariamente $b=7$, lo que nos dice que $a$ es impar. Hemos reducido los casos posibles a los siguientes:
- Si $(a,c)=(3,8)$, entonces $n=378$ y $97a-11b-200c=-1386$.
- Si $(a,c)=(5,6)$, entonces $n=576$ y $97a-11b-200c=-792$.
- Si $(a,c)=(7,4)$, entonces $n=774$ y $97a-11b-200c=-198$.
- Si $(a,c)=(9,2)$, entonces $n=972$ y $97a-11b-200c=396$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre