Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Si sumamos el número de cuadrados multiplicado por $4$, el número de hexágonos multiplicado por $6$ y el de octógonos multiplicado por $8$ obtendremos $3V$, siendo $V$ el número total de vértices. Por lo tanto, \[V=\frac{12\cdot 4+6\cdot 8+8\cdot 6}{3}=48.\] Ahora bien, de cada vértice salen tres aristas, una diagonal de un cuadrado, tres diagonales de un hexágono y 5 diagonales de un octógono, por lo que este vértice estará unido a otros $48-1-3-5=40$ vértices por segmentos interiores. Esto nos da un total de $40\cdot 48$ de tales segmentos, pero cada uno lo estamos contando dos veces (una por cada uno de sus extremos). Por tanto, el número de segmentos que buscamos es $\frac{1}{2}\cdot 40\cdot 48=960$.

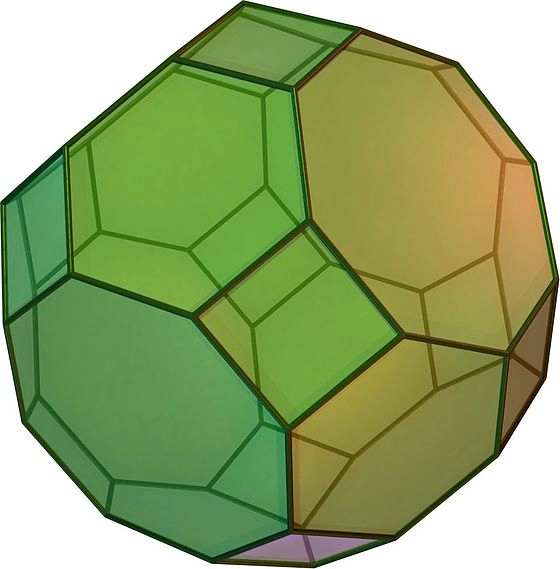
Nota. El poliedro en cuestión existe y se llama cuboctaedro truncado. Puede verse en la figura de arriba (extraída de Wikipedia). ¿Sabrías contar el número de aristas? ¿Sabrías probar que es el único poliedro tal que en cada vértice concurren un cuadrado, un hexágono y un octógono? En otras palabras, los datos de 12 cuadrados, 8 hexágonos y 6 octógonos son redundantes.

Solución. Vamos a ver que es imposible incluso si son de distinto tamaño por reducción al absurdo. Si el cubo se pudiera descomponer en un cierto número (finito) de tetraedros, como tales tetraedros definirán un número finito de vértices, habrá algún punto $P$ de una arista del cubo donde no llegará ningún vértice de ninguno de los tetraedros, lo que nos dice que a $P$ sólo llegan aristas de los tetraedros (no pueden llegar puntos interiores ni interiores a las caras ya que en tal caso los tetraedros se saldrían del cubo). De hecho, las aristas tienen que estar contenidas en las aristas del cubo, lo que nos dice que el ángulo diedro de $90^\circ$ que forman las dos caras del cubo que se encuentran en $P$ debe ser suma de un cierto número de veces el ángulo diedro $\alpha$ que forman las caras de un tetraedro regular $T$.

Para calcular $\alpha$, podemos suponer que $T$ tiene lado $1$. Seccionando $T$ por un plano que contiene a una de sus aristas y al punto medio de la arista opuesta. El triángulo en la intersección es isósceles y tiene un lado de longitud $1$, la arista de $T$, y los otros dos de longitud $\frac{\sqrt{3}}{2}$, la altura de una de las caras de $T$. El ángulo que buscamos es el que forman estos dos lados iguales, que puede calcularse como \[\alpha=2\,\mathrm{arcsen}\left(\frac{1/2}{\sqrt{3}/2}\right)=2\,\mathrm{arcsen}\left(\frac{1}{\sqrt{3}}\right)\gt 2\,\mathrm{arcsen}\left(\frac{1}{2}\right)=60^\circ.\] Además, está claro que $\alpha\lt 90^\circ$, por lo que no pueden completarse $90^\circ$ sumando un cierto número entero de ángulos iguales a $\alpha$.

Solución. El ejemplo que se nos viene a la cabeza cuando pensamos en que haya muchas ternas aditivas es el conjunto $A=\{1,2,3,\ldots,20\}$ de los primeros 20 números naturales. En este caso, la condición $a+b=c$ nos dice que $1\leq a\leq 19$ y, para cada valor de $a$, tenemos que $1\leq b\leq 20-a$. Por tanto, para $a=1$ tenemos 19 posibles valores de $b$, para $a=2$ tenemos 18, para $a=3$ tenemos 17, y así sucesivamente hasta $a=19$, donde tenemos la única posible elección $b=1$. Ahora bien, nos piden que los números $a,b,c$ tienen que ser distintos; como $c=a+b$ no puede ser igual a $a$ o $b$, tendremos que quitar las 10 sumas en que $a=b$, es decir, $1+1,2+2,\ldots,10+10$. Así, el número de ternas aditivas de $A$ es igual a $19+18+\ldots+1-10=\frac{19\cdot 20}{2}-10=180$.

Veremos ahora que ningún conjunto $B$ de $20$ naturales puede tener más de $180$ ternas aditivas. Pongamos $B=\{n_1,n_2,\ldots,n_{20}\}$ y supongamos que $0\lt n_1\lt n_2\lt\ldots\lt n_{20}$. Al expresar $n_k$ como $n_i+n_j$, se tiene necesariamente que $n_i,n_j\lt n_k$ y, para cada $n_i\lt n_k$, existe a lo sumo un $n_j\lt n_k$ tal que $n_i+n_j=n_k$. Así, podemos separar parejas de elementos de $\{n_1,n_2,\ldots,n_{k-1}\}$ que sumen $n_k$. Si $k=1$ o $k=2$, entonces no hay parejas que sumen $n_k$. Si $k\geq 3$ es impar, entonces habrá a lo sumo las $k$ parejas $(n_1,n_{k-1})$, $(n_2,n_{k-2}),\ldots,(n_{k-1},n_1)$. Si $k\geq 4$ es par, entonces algún elemento menor que $n_k$ quedará sin pareja y habrá a lo sumo $k-2$ parejas. Cuando $k$ se mueve de $1$ a $20$, esto nos da un máximo de \[0+0+2+2+4+4+\ldots +18+18=4(1+2+\ldots+9)=180\] posibles elecciones para el par $(a,b)$.

Nota. Observemos que da igual si consideramos 0 como natural o no pues no puede formar parte de una terna aditiva (tendríamos $(a,0,a)$ o $(0,b,b)$ y dos de los números serían iguales. Por otro lado, no es difícil completar el razonamiento de la segunda parte para demostrar que los conjuntos de 20 elementos que tienen exactamente 180 ternas aditivas son los de la forma $A=\{n,2n,\ldots,20n\}$ para cualquier $n\in\mathbb{N}$.

Solución. Si consideramos las nuevas variables $s=x+y$ y $p=xy$ (suma y producto), el sistema se puede reescribir como \[\left\{\begin{array}{l}s^2-3p=7,\\sp=-2.\end{array}\right.\] Despejamos $p=\frac{s^2-7}{3}$ en la primera ecuación y sustituimos en la segunda para obtener $(s^2-7)s=-6$ o, lo que es lo mismo, $s^3-7s+6=0$. Por Ruffini obtenemos rápidamente la factorización $s^3-7s+6=(s-1)(s-2)(s+3)$, lo que nos da tres posibilidades:

• Si $s=1$, entonces $p=\frac{s^2-7}{3}=-2$. Ahora bien, conociendo la suma y el producto, las incógnitas originales $x$ e $y$ son las soluciones de la ecuación $z^2-sz+p=0$. En este caso, esta última ecuación es $z^2-z-2=0$, que tiene soluciones $z=-1$ y $z=2$, lo que nos da las soluciones $(x,y)=(-1,2)$ y $(x,y)=(2,-1)$.
• Si $s=2$, entonces $p=\frac{s^2-7}{3}=-1$, luego $x$ e $y$ son las soluciones de $z^2-2z-1=0$, que son $z=1\pm\sqrt{2}$. Esto nos da otras dos soluciones al sistema: $(x,y)=(1+\sqrt{2},1-\sqrt{2})$ y $(x,y)=(1-\sqrt{2},1+\sqrt{2})$.
• Si $s=-3$, entonces $p=\frac{s^2-7}{3}=\frac{2}{3}$, luego $x$ e $y$ son las soluciones de $z^2+3z+\frac{2}{3}=0$, es decir, $z=\frac{-1}{6}(9\pm\sqrt{57})$. Esto nos da las dos últimas soluciones al sistema: $(x,y)=(frac{1}{6}(9+\sqrt{57}),frac{-1}{6}(9-\sqrt{57}))$ y $(x,y)=(frac{-1}{6}(9-\sqrt{57}),frac{-1}{6}(9+\sqrt{57}))$.

Esto nos da un total de seis soluciones al sistema.

Nota. En los sistemas de ecuaciones con dos incógnitas que son polinómicos y simétricos (cambiar $x$ por $y$ no afecta al sistema), cambiar a la suma-producto suele simplificar la discusión. En cualquier caso, es muy importante saber que tener la suma y el producto equivale a tener las dos incógnitas a través de la ecuación de segundo grado.

Solución. La primera parábola se puede expresar completando el cuadrado como \[y=ax^2+bx+c=\frac{(2ax+b)^2+(4ac-b^2)}{4a},\] de forma que su vértice tiene coordenadas $(x,y)=(\frac{-b}{2a},\frac{4ac-b^2}{4a})$ ya que este es el punto en el que el cuadrado toma su mínimo valor (cero). De la misma forma, el vértice de la segunda parábola tiene coordenadas $(\frac{-c}{2b},\frac{4ab-c^2}{4b})$, por lo que se tienen que verificar simultáneamente las siguientes dos ecuaciones: \[\frac{-b}{2a}=\frac{-c}{2b},\qquad c-\frac{b^2}{4a}=a-\frac{c^2}{4b}.\qquad(\star)\] La primera ecuación nos dice que $c=\frac{b^2}{a}$, luego podemos sustituir en la segunda para transformarla después de simplificar en \[\frac{b^2}{a}-\frac{b^2}{4a}=a-\frac{b^3}{4a^2}\ \Leftrightarrow\ 4a^3-3ab^2-b^3=0\ \Leftrightarrow\ (b-a)(2a+b)^2=0.\] Como $a\neq b$, deducimos que $b=-2a$, luego $c=\frac{b^2}{a}=4a$. Tenemos así que las parábolas que las ternas que resuelven el problema tienen que ser de la forma $(a,-2a,4a)$ para cualquier $a\neq 0$. Fácilmente se ve que todas estas cumplen las ecuaciones marcadas con $(\star)$.