Encontrar, razonadamente, dos números enteros positivos $a$ y $b$, tales que $b^2$ sea múltiplo de $a$, $a^3$ sea múltiplo de $b^2$, $b^4$ sea múltiplo de $a^3$ y $a^5$ sea múltiplo de $b^4$, pero de forma que $b^6$ no sea múltiplo de $a^5$.
pistasolución 1info
Pista. Toma los números como $a=p^x$ y $b=p^y$, siendo $p$ un número primo y $x,y$ exponentes naturales. ¿Qué desigualdades deben cumplir $x$ e $y$ para verificar las condiciones dadas en el enunciado?
Solución. Consideremos un primo $p$ y tomemos los números $a=p^x$ y $b=p^y$ para ciertos exponentes enteros positivos $x$ e $y$. Las condiciones del enunciado se traducen como sigue:
\begin{align*}
b^2\text{ es múltiplo de }a&\ \Longleftrightarrow\ 2y\geq x,\\
a^3\text{ es múltiplo de }b^2&\ \Longleftrightarrow\ 3x\geq 2y,\\
b^4\text{ es múltiplo de }a^3&\ \Longleftrightarrow\ 4y\geq 3x,\\
a^5\text{ es múltiplo de }b^4&\ \Longleftrightarrow\ 5x\geq 4y,\\
b^6\text{ no es múltiplo de }a^5&\ \Longleftrightarrow\ 6y\lt 5x.
\end{align*}
La primera y tercera desigualdades nos dicen que $y\geq\frac{1}{2}x$ e $y\geq\frac{3}{4}x$. Podemos quedarnos solamente con $y\geq\frac{3}{4}x$ pues todo número que cumpla esta desigualdad también cumplirá la otra. Análogamente, la segunda, cuarta y quinta desigualdades nos dicen que $y\leq\frac{3}{2}x$, $y\leq\frac{5}{4}x$ e $y\lt\frac{5}{6}x$, de las cuales ahora la más restrictiva es $y\lt\frac{5}{6}x$ y podemos eliminar las otras dos.
Todo esto nos dice que buscamos números $x$ e $y$ tales que $\frac{3}{4}x\leq y\lt\frac{5}{6}x$ o, lo que es lo mismo, $18x\leq 24y\lt 20x$. Hay muchas soluciones a esta desigualdad y solo buscamos una, por ejemplo, $y=3$ y $x=4$. Deducimos que los números $a=p^4$ y $b=p^3$ cumplen la condición del enunciado.
Nota. De hecho, se puede probar que $a=16$ y $b=8$ son los números más pequeños que cumplen el enunciado. ¿Sabrías demostrar por qué?
En el triángulo $ABC$ se traza la bisectriz interior $CD$. Se sabe que el centro del círculo inscrito en el triángulo $BCD$ coincide con el centro del círculo circunscrito del triángulo $ABC$. Calcular los ángulos del triángulo $ABC$.
pistasolución 1info
Pista. Calcula los ángulos del triángulo $OBC$, siendo $O$ el circuncentro de $ABC$.
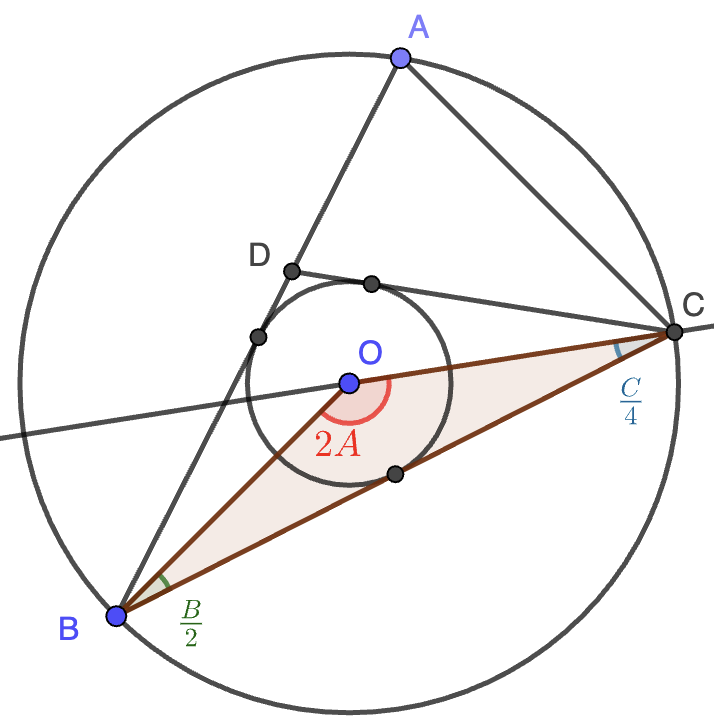
Solución. Consideramos el circuncentro $O$ y el triángulo $OBC$, que está sombreado en la figura. Por un lado, tenemos que $\angle BCD=\frac{C}{2}$, por ser $BD$ la bisectriz, luego $\angle OCB=\frac{C}{4}$ ya que $OC$ es bisectriz del triángulo $BCD$. Por otro lado, tenemos que $\angle OBC=\frac{B}{2}$ ya que $OB$ es bisectriz de $BCD$. Finalmente, tenemos que $\angle BOC=2A$ ya que se trata del ángulo central del ángulo $A$ en el triángulo $ABC$.
Tenemos así que $OBC$ tiene ángulos $2A$, $\frac{B}{2}$ y $\frac{C}{4}$. Este triángulo es isósceles dado que $OB=OC$ (son el radio de la circunferencia circunscrita), luego $\frac{C}{4}=\frac{B}{2}$. Nos quedan por tanto, tres ecuaciones sobre las incógnitas $A,B,C$, que forman el sistema lineal:
\[\left\{\begin{array}{c}
A+B+C=180\\
2A+\frac{B}{2}+\frac{C}{4}=180\\
\frac{C}{4}=\frac{B}{2}
\end{array}\right.\]
Se resuelve fácilmente, dando solución única $A=C=72^\circ$ y $B=36^\circ$.
Supongamos que las ecuaciones de segundo grado
\begin{align*}
x^2+a_1x+b_1&=0,\\
x^2+a_2x+b_2&=0,\\
\vdots&\\
x^2+a_nx+b_n&=0,
\end{align*}
tienen una raíz común $x_0$. Hallar las raíces de la ecuación
\[x^2+\frac{a_1+a_2+\ldots+a_n}{n}x+\frac{b_1+b_2+\ldots+b_n}{n}=0\]
en términos de $x_0$ y del resto de raíces de las ecuaciones iniciales.
pistasolución 1info
Pista. Suma las $n$ ecuaciones para obtener que $x_0$ también es solución de la ecuación con las medias aritméticas.
Solución. Teniendo en cuenta que $x_0^2+a_ix_0+b_i=0$ para todo $i$, podemos sumar estas $n$ igualdades (para $i$ entre $1$ y $n$) y nos queda
\[nx_0^2+(a_1+a_2+\ldots+a_n)x_0+(b_1+b_2+\ldots+b_n)=0.\]
Dividiendo por $n$, concluimos que $x_0$ también es solución de la ecuación con las medias aritméticas. Para calcular la otra solución, vamos a dividir el polinomio
\[P(x)=x^2+\frac{a_1+a_2+\ldots+a_n}{n}x+\frac{b_1+b_2+\ldots+b_n}{n}\]
entre $x-x_0$ (esto es muy fácil usando Ruffini), lo que nos da
\[P(x)=(x-x_0)(x+\tfrac{a_1+a_2+\ldots+a_n}{n}+x_0)\]
Si llamemos $x_i$ a la otra solución de la ecuación $x^2+a_ix+b_i=0$ que no es $x_0$, tenemos que $a_i=-(x_0+x_i)$ con lo que la otra raíz de $P(x)$ es
\begin{align*}
-\frac{a_1+a_2+\ldots+a_n}{n}-x_0&=\frac{x_1+x_0+x_2+x_0+\ldots+x_n+x_0}{n}-x_0\\
&=\frac{x_1+x_2+\ldots+x_n}{n},
\end{align*}
es decir, la media aritmética de las raíces de las ecuaciones originales.
Sea $ABC$ un triángulo rectángulo isósceles con el ángulo recto en $C$ y los catetos de longitud $2$. Un arco de círculo $\ell$ con centro $A$ divide al triángulo en dos partes de la misma área, mientras que el arco de círculo $m$ con centro en $B$ es tangente a $\ell$ en un punto de la hipotenusa $AB$. Hallar el área de la porción del triángulo no cubierta por los sectores circulares correspondientes a los dos arcos.
pistasolución 1info
Pista. Calcula primero el radio del arco $\ell$ y luego el radio del arco $m$, con lo que podrás calcular el área de los sectores circulares.
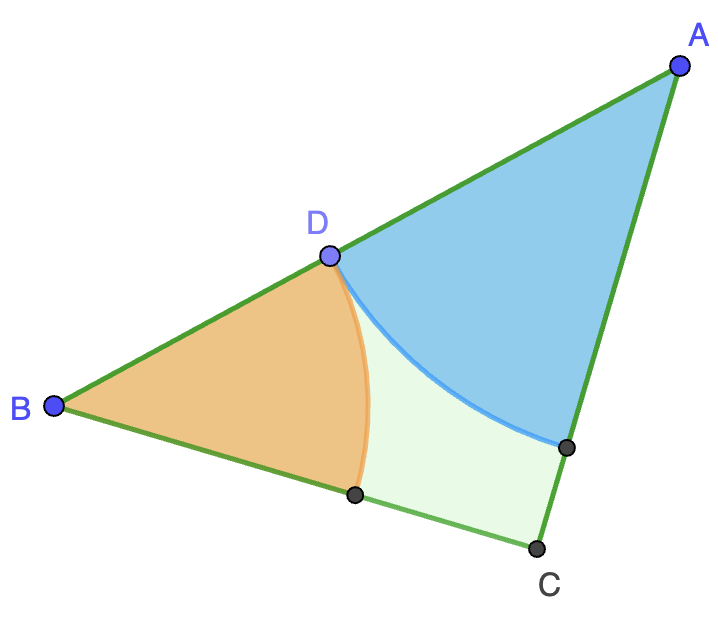
Solución. El área del triángulo es $2$ y el área del sector circular de arco $\ell$ (en azul en la figura) es $\frac{1}{8}\pi r^2$, siendo $r$ su radio. Esto viene de que es un octavo del círculo de radio $r$ ya que el ángulo $A$ del triángulo rectángulo isósceles $ABC$ es $45^\circ$. Igualando a la mitad del área del triángulo, obtenemos
\[\tfrac{1}{8}\pi r^2=1\ \Longleftrightarrow\ r=2\sqrt{\tfrac{2}{\pi}}.\]
Observamos que $r\lt 2$, lo que nos dice que el sector realmente está bien definido. Ahora bien, el radio $s$ del sector de arco $m$ (en naranja en la figura) sumado con $r$ nos da la hipotenusa $AB=2\sqrt{2}$, luego podemos despejar
\[s=AB-r=2\sqrt{2}-2\sqrt{\tfrac{2}{\pi}}=2\sqrt{2}(1-\tfrac{1}{\sqrt{\pi}}).\]
Tenemos entonces que el área que nos piden (en verde en la figura) es
\[2-\tfrac{\pi}{8}r^2-\tfrac{\pi}{8}s^2=2-1-\tfrac{8\pi}{8}(1-\tfrac{1}{\sqrt{\pi}})^2=2\sqrt{\pi}-\pi.\]
Sea $M=\{1,2,\ldots,49\}$ el conjunto de los primeros 49 enteros positivos. Determinar el máximo entero $k$ tal que el conjunto $M$ tiene un subconjunto de $k$ elementos en el que no hay $6$ números consecutivos. Para este valor máximo de $k$, hallar la cantidad de subconjuntos de $M$ de $k$ elementos que tienen la propiedad mencionada.
pistasolución 1solución 2info
Pista. Demuestra que una forma de obtener el máximo es omitir los múltiplos de 6, pero no es la única ya que hay cierta flexibilidad en qué números se omiten.
Solución. Si quitamos los ocho múltiplos de $6$ nos quedan $41$ números que cumplen la propiedad ya que hemos dejado ocho bloques de 5 números consecutivos más el número 49 aislado. Veamos que si se omiten sólo 7 números, entonces tienen que quedar seis consecutivos, lo que nos dirá que $41$ es la respuesta. Si vemos estos siete números como separadore, los otros 42 números restantes quedarán separados en 8 grupos de números consecutivos. Si los 8 grupos tuvieran 5 o menos números, entonces tendríamos máximo $5\cdot 8=40$, pero hay 42, lo que nos dice que habrá 6 o más consecutivos (principio del palomar).
Veamos finalmente cuántos subconjuntos de $41$ elementos tienen la propiedad. Al igual que antes, al omitir 8 números, podemos transformar el problema en elegir 9 números $a_1,a_2,\ldots,a_9$ entre $1$ y $5$ que dirán la cantidad de números consecutivos que habrá entre cada uno de los 8 que se omiten. Como tiene que ser $a_1+a_2+\ldots+a_9=41$, podemos pensar en hacer $a_1=a_2=\ldots=a_9=5$ (el máximo) y luego restarle $1$ a cuatro de los nueve números (posiblemente con repetición). Esto no son más que combinaciones con repetición, que equivalen a su vez a elegir como separadores 9 elementos de un conjunto de $4+9=13$ elementos. Por tanto, tenemos un total de $\binom{13}{9}=\binom{13}{4}=715$ subconjuntos de $41$ elementos con la propiedad del enunciado.
Solución. Veamos en primer lugar cómo conseguir el máximo usando un razonamiento voraz. Supongamos que $k$ es el máximo y que $S$ es un subconjunto de $k$ elementos en el que no hay 6 números consecutivos. Tenemos dos propiedades importantes:
- Si $S$ omitiera dos o más números consecutivos $n,n+1,\ldots,n+a$, entonces podríamos restarle $a$ unidades a todos los elementos de $S$ mayores que $n+a$ y tendríamos un conjunto $S'$ con el mismo número de elementos y también cumpliendo la propiedad. Si $n+a=49$, podríamos añadirle más números a partir del $n+1$ y tendríamos $S'$ con más elementos, luego $S$ no sería el conjunto de más elementos.
- Si $S$ no contiene dos números $n$ y $n+a$ pero sí los intermedios $n+1,\ldots,n+a-1$, entonces tiene que ser $a\leq 6$ para que haya máximo cinco consecutivos. Si fuera $n+a\leq 6$, podemos añadir los números desde el $1$ hasta el $n$ y obtenemos un conjunto que cumple la propiedad con más elementos. Si fuera $a\lt 6$ (hay menos de 5 consecutivos), entonces podemos añadir $n+a$ al conjunto y sumarle una unidad a todos los elementos de $S$ mayores o iguales que $n+a$. Repitiendo el proceso, llegamos a un conjunto $S'$ con al menos el mismo número de elementos de $S$ y que tiene a $n+1,n+2,n+3,n+4,n+5$ pero no a $n$ ni $n+6$.
Estas idas nos dicen que un ejemplo de subconjunto $S\subset M$ con la mayor cantidad de números (sin 6 consecutivos) consiste en tomar 5 consecutivos, omitir el sexto, luego 5 consecutivos y omitir el sexto, y así sucesivamente. Como $49=8\cdot 6 +1$, tenemos que hay que omitir un mínimo de 8 números y que el mayor valor de $k$ es $49-8=41$.
Vamos ahora a contar cuántos subconjuntos de $41$ elementos tienen esta propiedad. La idea es que, al omitir 8 números, podemos transformar el problema en elegir 9 números $a_1,a_2,\ldots,a_9$ entre $1$ y $5$ que dirán la cantidad de números consecutivos que habrá entre cada uno de los 8 que se omiten. Como tiene que ser $a_1+a_2+\ldots+a_9=41$, podemos pensar en hacer $a_1=a_2=\ldots=a_9=5$ (el máximo) y luego restarle $1$ a cuatro de los nueve números (posiblemente con repetición). Esto no son más que combinaciones con repetición, que equivalen a su vez a elegir como separadores 9 elementos de un conjunto de $4+9=13$ elementos. Por tanto, tenemos un total de $\binom{13}{9}=\binom{13}{4}=715$ subconjuntos de $41$ elementos con la propiedad del enunciado.


