Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 769
OIM, 2003-P6
Se definen las sucesiones $\{a_n\}$ y $\{b_n\}$ como
\begin{align*}
a_0&=1,& a_{n+1}&=a_n^{2001}+b_n,\\
b_0&=4,& b_{n+1}&=b_n^{2001}+a_n,
\end{align*}
para todo $n\geq 0$. Demostrar que 2003 no divide a ninguno de los términos de estas sucesiones.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 768
OIM, 2003-P5
En el cuadrado $ABCD$, sean $P$ y $Q$ puntos pertenecientes a los lados $BC$ y $CD$, respectivamente, distintos de los extremos y tales que $BP=CQ$. Se consideran puntos $X$ e $Y$, $X\neq Y$, pertenecientes a los segmentos $AP$ y $AQ$, respectivamente. Demuestre que, cualesquiera que sean $X$ e $Y$, existe un triángulo cuyos lados tienen las longitudes de $BX$, $XY$ y $DY$.
pistasolución 1info
Pista. Dobla el papel en el que has dibujado el cuadrado.
Solución. Si recortamos el cuadrado y también el triángulo $CPQ$, podemos doblar por las líneas $AP$ y $AQ$ para formar una pirámide con vértice en $A$. Observemos que, de esta forma $B$ se identifica con $D$ ya que ambos puntos están a la misma distancia de $A$. No obstante, para comprobar que efectivamente la pirámide se cierra, observamos que el triángulo de vértices $B=D$, $P$ y $Q$ en el espacio es rectángulo ya que es congruente con el triángulo $CPQ$ que hemos quitado. Ahora la solución al problema es evidente ya que $BX$, $XY$ y $DY$ forman un triángulo en el espacio.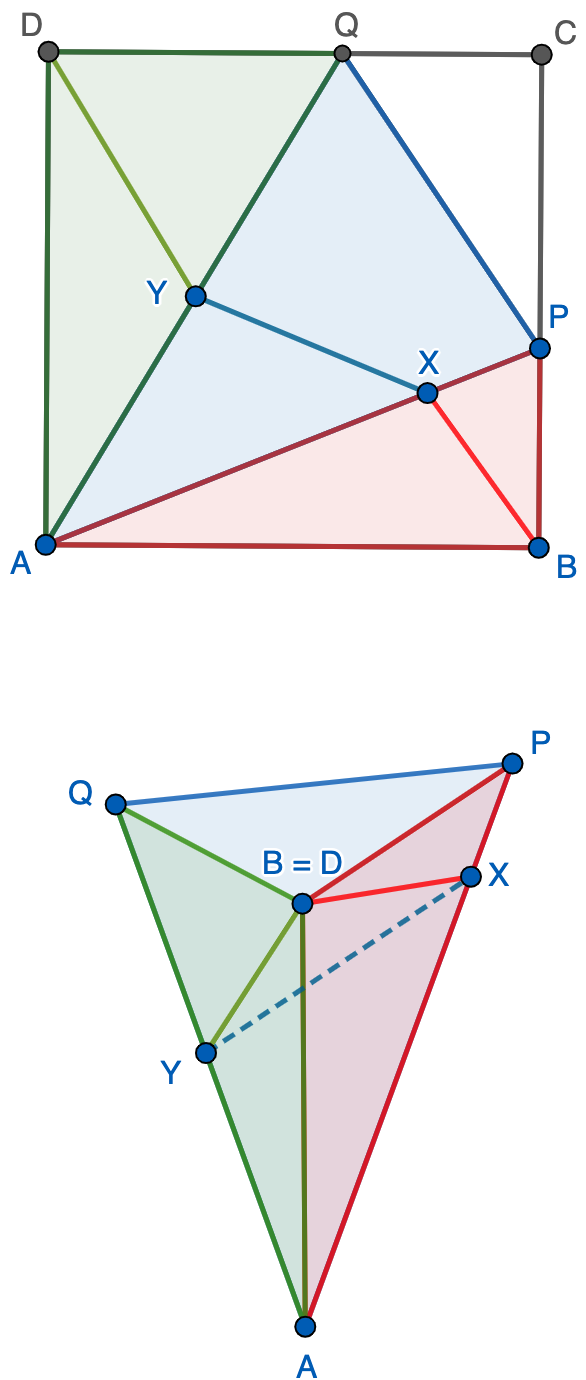

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 767
OIM, 2003-P2
Sean $C$ y $D$ dos puntos de la semicircunferencia de diámetro $AB$ tales que $B$ y $C$ están en semiplanos distintos respecto de la recta $AD$. Denotemos por $M$, $N$ y $P$ los puntos medios de $AC$, $DB$ y $CD$, respectivamente. Sean $O_A$ y $O_B$ los circuncentros de los triángulos $ACP$ y $BDP$. Demostrar que las rectas $O_AO_B$ y $MN$ son paralelas.
pistasolución 1info
Pista. Demuestra que $OO_AO_B$ y $OMN$ son semejantes, siendo $O$ el centro de la semicircunferencia. Te puede ser útil utilizar el teorema de Thales.
Solución. Las mediatriz de $AC$ pasa por $O_A$ y por el centro $O$ de la semicircunferencia y, de la misma forma, la mediatriz de $BD$ pasa por $O_B$ y por $O$. Por tanto, que $O_AO_B$ sea paralela a $MN$ equivale a que los triángulos $OO_AO_B$ y $OMN$ sean semejantes. Si trazamos perpendiculares a la recta $CD$ que pasan por $A$, $M$, $O_A$, $O_B$, $N$ y $B$ (en línea discontinua en la figura) y marcamos los puntos de intersección con $CD$ como $E$, $F$, $G$, $H$, $I$ y $J$, respectivamente, el teorema de Thales nos dice que
\[\frac{OO_A}{GP}=\frac{OM}{PF},\qquad \frac{OO_B}{HP}=\frac{ON}{PI}.\]
Utilizando que $G$ y $H$ son los puntos medios de $CP$ y $DP$ (ya que las perpendiculares por $O_A$ y $O_B$ son mediatrices de $CP$ y $DP$, respectivamente), las semejanzas anteriores se reescriben como
\[\frac{OO_A}{OM}=\frac{CP}{2PF},\qquad \frac{OO_B}{ON}=\frac{DP}{2PI}.\]
Como $CP=DP$ por ser $P$ el punto medio de $CD$, el problema estará resuelto si demostramso que $PF=PI$. Usando de nuevo que $CP=DP$, podemos reducir el problema aún más a probar que $PE=PJ$, pero esto último es sencillo ya que es consecuencia del teorema de Thales aplicado a las paralelas $BJ$, $OP$ y $AE$ que cortan a las rectas $AB$ y $AJ$, teniendo en cuenta que $O$ es el punto medio de $AB$.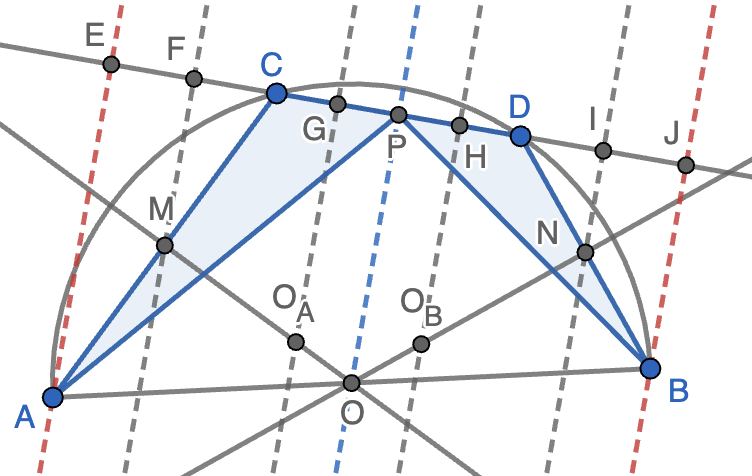

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 766
OIM, 2002-P6
Un policía intenta capturar a un ladrón en un tablero $2001\times 2001$. Cada uno de ellos, por turnos, deben moverse una casilla en uno de los tres siguientes sentidos:
\[\downarrow\text{ (abajo),}\quad \to\text{ (derecha),}\quad \nwarrow \text{(diagonal superior izquierda).}\]
Si el policía se encuentra en la casilla de la esquina inferior derecha, puede usar su jugada para pasar directamente a la casilla de la esquina superior izquierda (el ladrón no puede hacer esta jugada). Inicialmente, el policía está en la casilla central y el ladrón está en la casilla vecina diagonal superior derecha al policía. El policía comienza el juego. Demostrar las siguientes afirmaciones:
- El ladrón consigue moverse por lo menos $10000$ veces sin ser capturado.
- El policía posee una estrategia para capturar al ladrón.
Nota. El policía captura al ladrón cuando entra en la casilla en la que está el ladrón. Si el ladrón entra en la casilla del policía, no se produce captura.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 765
OIM, 2002-P5
La sucesión de números reales $\{a_1,a_2,\ldots,a_n,\ldots\}$ se define como
\[a_1=56,\qquad a_{n+1}=a_n-\frac{1}{a_n},\text{ para todo }n\geq 1.\]
Demostrar que existe un número entero $k$, $1\leq k\leq 2002$, tal que $a_k\lt 0$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre