Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 749
OIM, 1998-P3
Hallar el mínimo número natural $n$ con la siguiente propiedad: entre cualesquiera $n$ números distintos del conjunto $\{1,2,\ldots,999\}$ se pueden elegir cuatro números diferentes $a,b,c,d$ tales que $a+2b+3c=d$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 748
OIM, 1998-P2
La circunferencia inscrita de un triángulo $ABC$ es tangente a los lados $BC$, $CA$ y $AB$ en los puntos $D$, $E$ y $F$, respectivamente. $AD$ corta la circunferencia en un segundo punto $Q$. Demostrar que la recta $EQ$ pasa por el punto medio de $AF$ si y solamente si $AC = BC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 747
La figura se compone de seis pentágonos regulares de lado 1. Se dobla por las líneas de puntos hasta que coincidan las aristas no punteadas que confluyen en cada vértice. ¿Qué volumen de agua cabe en el recipiente formado?
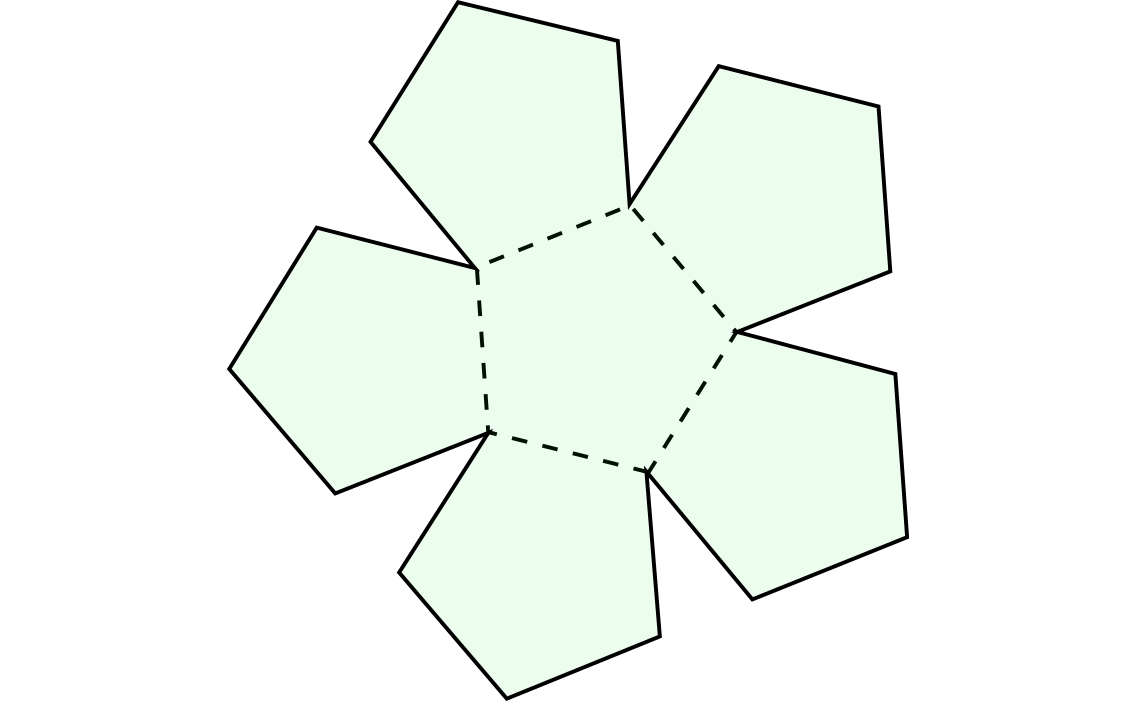
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 746
En Port Aventura hay 16 agentes secretos. Cada uno de ellos vigila a algunos de sus colegas. Se sabe que si el agente $A$ vigila al agente $B$, entonces $B$ no vigila a $A$. Además, 10 agentes cualesquiera pueden ser numerados de forma que forman un ciclo: el primero vigila al segundo, éste vigila al tercero y así hasta que el décimo vigila al primero. Demostrar que también se pueden numerar de este modo 11 agentes cualesquiera.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 745
Discutir la existencia de soluciones de la ecuación
\[\sqrt{x^2-p}+2\sqrt{x^2-1}=x\]
según los valores del parámetro $p\in\mathbb{R}$ y resolverla siempre que sea posible.
pistasolución 1info
Pista. Puedes dividir por $x$ para simplificar (observando previamente que ha de ser $x\geq 1$). Elevando varias veces al cuadrado, deberías obtener la solución. también puedes transformar en un sistema asignándole una variable nueva a cada raíz.
Solución. Observamos que tiene que ser $x\gt 0$ ya que el miembro de la izquierda no puede ser negativo, luego $x\geq 1$ para que la segunda raíz esté definida. Dividiendo entre $x$ ambos miembros y escribiendo $t=\frac{1}{x^2}$, la ecuación se reescribe como
\[\sqrt{1-pt}+2\sqrt{1-t}=1.\]
Si llamamos $y=\sqrt{1-pt}$ y $z=\sqrt{1-t}$, podemos reescribirlo de nuevo como el sistema
\[\left\{\begin{array}{l}y+2z=1\\y^2-pz^2=1-p\end{array}.\right.\]
Despejamos $y=1-2z$ en la primera ecuación y sustituimos en la segunda, lo que nos da una ecuación de segundo grado en $z$:
\[(1-2z)^2-pz^2=1-p\ \Longleftrightarrow\ 4z^2-(p+4)z+p=0.\]
Esta ecuación tiene soluciones $z=1$ y $z=\frac{p}{4-p}$. La primera hay que descartarla ya que nos lleva a que $\frac{1}{x^2}=t=0$, que no tiene soluciones. Para $z=\frac{p}{4-p}$, podemos despejar
\[\frac{1}{x^2}=t=1-z^2=1-\frac{p^2}{(4-p)^2}=\frac{8(2-p)}{(4-p)^2}.\]
Por tanto, tiene que ser $p\leq 2$, lo que nos da la única candidata a solución:
\[x=\frac{4-p}{2\sqrt{2}\sqrt{2-p}}.\]
Comprobamos ahora si cumple la condición:
\[\sqrt{x^2-p}+2\sqrt{x^2-1}=\sqrt{\frac{(4-3p)^2}{8(2-p)}}+2\sqrt{\frac{p^2}{8(2-p)}}=\frac{|4-3p|+2|p|}{2\sqrt{2}\sqrt{2-p}}.\]
La única forma de que el numerador anterior sea igual a $4-p$ (para que el resultado de la operación sea $x$), es que $4-3p\geq 0$ y $p\geq 0$, lo que nos dice que la ecuación tiene solución si y sólo si $0\leq p\leq \frac{4}{3}$, en cuyo caso la solución es única.
Nota. Otra forma de ver la existencia y unicidad de solución (aunque no de calcularla) es usar el teorema de Bolzano. La función $f(t)=\sqrt{1-pt}+2\sqrt{1-t}-1$ es continua y estrictamente decreciente. Nos interesa su valor en $[0,\min\{1,\frac{1}{p}\}]$. Tenemos que $f(0)=2\gt 0$. Si $p\geq 1$, entonces evaluamos $f(\frac{1}{p})=2\sqrt{1-\frac{1}{p}}-1$, que es negativo si y sólo si $p\leq\frac{4}{3}$. Si $p\leq 1$, entonces $f(1)=\sqrt{1-p}-1$ es negativo siempre que $p\gt 0$. En resumen, tenemos que $0\leq p\leq \frac{4}{3}$ y que la solución es única.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre