Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Informar de error en enunciado Informar de procedencia del problema
A la hora de calcular los perímetros, tenemos que hay $100$ elecciones para $a$, $100$ para $b$ y $100$ para $c$ de forma independiente (nos dicen que elijamos tres números ordenados del conjunto), luego hay $100^3=10^6$ posibilidades para la terna $(a,b,c)$, lo que nos da $3\cdot 10^6$ lados de triángulos. Como cada uno de los elementos $a_1,\ldots,a_{100}$ se usa el mismo número de veces, tendremos que usar $3\cdot 10^4$ veces cada uno de ellos y será $S(A)=3\cdot 10^4\cdot (a_1+a_2+\ldots+a_{100})$. Como entre $a_1$ y $\sqrt{2}a_1$ deben caber otros $99$ enteros distintos, ha de cumplirse que $a_1\sqrt{2}\geq a_1+99$, o equivalentemente $a_1\geq\frac{99}{\sqrt{2}-1}\approx 239.007$. El valor mínimo de $S(A)$ se obtiene tomando $a_1=240$, $a_2=241$,... y así hasta $a_{100}=339$. Esto nos da el valor mínimo \begin{align*} S(A)&=3\cdot 10^4\cdot (240+241+\ldots+339)\\ &=3\cdot 10^4\cdot (100\cdot 240+1+\ldots+99)\\ &=30000\cdot (24000+\tfrac{99\cdot 100}{2})=868500000. \end{align*}
Nota. En un triángulo de lados $a,b,c$, el ángulo $\alpha$ opuesto al lado $a$ verifica la siguiente igualdad por el teorema del coseno: \[a^2=b^2+c^2-2bc\cos(A)\ \Longleftrightarrow\ \cos(A)=\frac{b^2+c^2-a^2}{2bc}.\] El ángulo es obtuso cuando su coseno es negativo, luego no será obtusángulo cuando $b^2+c^2\geq a^2$. Esta es la desigualdad que hemos aplicado al triángulo de lados $a_1,a_1,a_{100}$, teniendo en cuenta que el ángulo más grande es el opuesto al lado más grande, $a_{100}$.
Informar de error en enunciado Informar de procedencia del problema
- Calcular las medidas de los ángulos del triángulo $BCD$.
- Expresar la medida del lado $BC$ en función de la medida del lado $AC$, sin que en la expresión aparezcan razones trigonométricas.
El triángulo $ABD$ también es isósceles por tener dos ángulos iguales a $36^\circ$, luego $BC=BD=AD$. Además, $BCD$ y $ABC$ son semejantes por tener los ángulos iguales, luego
\[\frac{AC}{BC}=\frac{BC}{CD}=\frac{BC}{AC-AD}=\frac{BC}{AC-BC}.\]
De esta igualdad, obtenemos que $AC^2-AC\cdot BC-BC^2=0$. Dividiendo entre $AC^2$, llegamos a la ecuación de segundo grado
\[\left(\frac{BC}{AC}\right)^2+\frac{BC}{AC}-1=0\ \Longrightarrow\ \frac{BC}{AC}=\frac{-1\pm\sqrt{5}}{2}.\]
Tenemos que descartar la solución negativa, lo que nos dice finalmente que
\[BC=\frac{\sqrt{5}-1}{2}AC.\]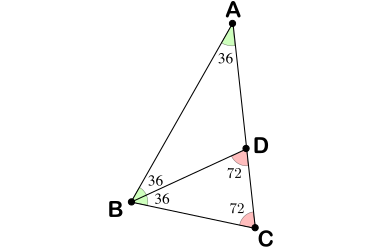
Informar de error en enunciado Informar de procedencia del problema
| Región | Soleados o lluviosos | Inclasificables |
|---|---|---|
| A | 336 | 29 |
| B | 321 | 44 |
| C | 335 | 30 |
| D | 343 | 22 |
| E | 329 | 36 |
| F | 330 | 35 |
Nota. En realidad, el argumento no prueba que el número de días lluviosos es la tercera parte del de soleados, sino que se basa en que la persona encargada sabe que esto ocurre para alguna región. Hemos visto que solo puede ser la F.
Informar de error en enunciado Informar de procedencia del problema
- El lugar geométrico de $W$ es el conjunto de ecuación $x+y=\frac{k}{2}$ con $x,y,z\gt 0$, es decir, la intersección del plano $x+y=2k$ con el primer cuadrante.
- El lugar geométrico de $W$ es el conjunto de ecuación $x+y=\frac{k}{2}$ y $z=0$ con $x,y\gt 0$, es decir, el segmento de recta que une los puntos $(\frac{k}{2},0,0)$ y $(0,\frac{k}{2},0)$ en el plano $OXY$.
Informar de error en enunciado Informar de procedencia del problema