Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Numeramos las casillas del tablero del $0$ al $9$ siguiendo las diagonales: \[\begin{bmatrix} 0&1&2&3&4&5&6&7&8&9\\ 1&2&3&4&5&6&7&8&9&0\\ 2&3&4&5&6&7&8&9&0&1\\ 3&4&5&6&7&8&9&0&1&2\\ 4&5&6&7&8&9&0&1&2&3\\ 5&6&7&8&9&0&1&2&3&4\\ 6&7&8&9&0&1&2&3&4&5\\ 7&8&9&0&1&2&3&4&5&6\\ 8&9&0&1&2&3&4&5&6&7\\ 9&0&1&2&3&4&5&6&7&8 \end{bmatrix}\] Al colocar $41$ torres, por el principio del palomar al menos cinco de ellas compartirán el número que hay en su casilla. Estas torres no se atacan entre sí ya que ningún número se repite en ninguna fila ni columna.

Solución. Podemos completar los cuadrados en cada incógnita para expresar de forma equivalente la ecuación como \[(x-\tfrac{1}{2})^2-\tfrac{1}{4}+(y-\frac{3}{2})^2-\tfrac{9}{4}-(z+\tfrac{1}{2})^2+\tfrac{1}{4}=4.\] Tras pasar los términos independientes al miembro de la derecha y multiplicar por 4, tenemos la ecuación equivalente \[(2x-1)^2+(2y-3)^2-(2z+1)^2=25.\] Por tanto, tomando $z=x-1$ e $y=4$, tenemos la familia infinita de soluciones $(x,y,z)=(a,4,a-1)$ para cualquier entero $a$.

Solución. Pongamos que hay $a$ chicos y $b$ chicas. Si todos hubieran comido el mínimo, habrían hecho falta $6a+2b$ porciones, mientras que el máximo sería $7a+3b$. Por tanto, se tiene que cumplir que \[48\lt 6a+2b,\qquad 7a+3b\lt 60.\] Observamos que las desigualdades son estrictas porque se dice que faltó con cuatro pizzas y sobró con cinco. Sumando siete veces la primera desigualdad y seis la segunda, tenemos que $336+42a+18b\lt 42a+14b+360$, de donde $b\lt 6$, es decir $b\leq 5$. Distingamos casos:

• Si $b=1$, las desigualdades quedan $46\lt 6a$ y $7a\lt 57$, es decir, $\frac{46}{6}\lt a\lt\frac{57}{7}$ que tiene por única solución entera $a=8$.
• Si $b=2$, queda $44\lt 6a$ y $7a\lt 54$, que no tiene soluciones enteras.
• Si $b=3$, queda $42\lt 6a$ y $7a\lt 51$, que no tiene soluciones enteras.
• Si $b=4$, queda $40\lt 6a$ y $7a\lt 48$, que no tiene soluciones enteras.
• Si $b=5$, queda $38\lt 6a$ y $7a\lt 45$, que no tiene soluciones enteras.

Deducimos que hay dos soluciones al problema: 8 chicos y 1 chica o bien 7 chicos y 2 chicas.

Solución. Cambiando $x$ por $1-x$, tenemos la ecuación \[(1-x)^2f(1-x)+f(x)=2(1-x)-(1-x)^4.\] Esta ecuación es cierta para todo $x\in\mathbb{R}$ y, junto con la ecuación dada en el enunciado, nos da un sistema lineal de dos ecuaciones si vemos a $f(x)$ y $f(1-x)$ como incógnitas. Restando a esta última ecuación la primera multiplicada por $(1-x)^2$ eliminamos el término $f(1-x)$, lo que nos da \[f(x)-x^2(1-x)^2f(x)=2(1-x)-(1-x)^4-(1-x)^2(2x-x^4).\] Tras simplificar y factorizar (observamos que $1-x^2(1-x)^2$ es diferencia de cuadrados), podemos despejar \[f(x)=\frac{-(x-1)(x+1)(x^2-x-1)(x^2-x+1)}{(x^2-x-1)(x^2-x+1)}.\] El factor $x^2-x+1$ es siempre positivo ya que la ecuación $x^2-x+1=0$ no tiene soluciones. Sin embargo $x^2-x-1=0$ tiene soluciones $x=\frac{1}{2}(1\pm\sqrt{5})$ en cuyo caso no podemos simplificar este factor. Distinguimos dos casos:

• Si $x\neq\frac{1}{2}(1\pm\sqrt{5})$, entonces tras simplificar todos los factores comunes obtenemos que $f(x)=1-x^2$.
• Para el caso $x=\frac{1}{2}(1\pm\sqrt{5})$, sustituimos estos valores en la ecuación inicial, lo que nos da el siguiente sistema lineal en las incógnitas $a=\frac{1}{2}(1-\sqrt{5})$ y $b=\frac{1}{2}(1-\sqrt{5})$: \[\left\{\begin{array}{l}2a+(3+\sqrt{5})b=-5-\sqrt{5},\\ (3-\sqrt{5})a+2b=-5+\sqrt{5}\end{array}\right.\] Es fácil ver que es compatible indeterminado y que podemos despejar \[b=\frac{-5+\sqrt{5}-(3-\sqrt{5})a}{2},\] de forma que $a$ es un parámetro real arbitrario.

Con todo esto, las funciones que verifican la igualdad del enunciado son las de la forma \[f(x)=\begin{cases}1-x^2&\text{si }x\neq\frac{1}{2}(1\pm\sqrt{5}),\\ a&\text{si }x=\frac{1}{2}(1-\sqrt{5}),\\ \frac{-5+\sqrt{5}-(3-\sqrt{5})a}{2}&\text{si }x=\frac{1}{2}(1+\sqrt{5}),\end{cases}\] para cualquier $a\in\mathbb{R}$.

Nota. Este problema se ha marcado con 2,5 estrellas porque es realmente fácil omitir el caso $x=\frac{1}{2}(1\pm\sqrt{5})$ y decir que $f(x)=1-x^2$ para todo $x\in\mathbb{R}$ (este fallo está incluso en la solución oficial), que se corresponde con el caso $a=\frac{-1+\sqrt{5}}{2}$.

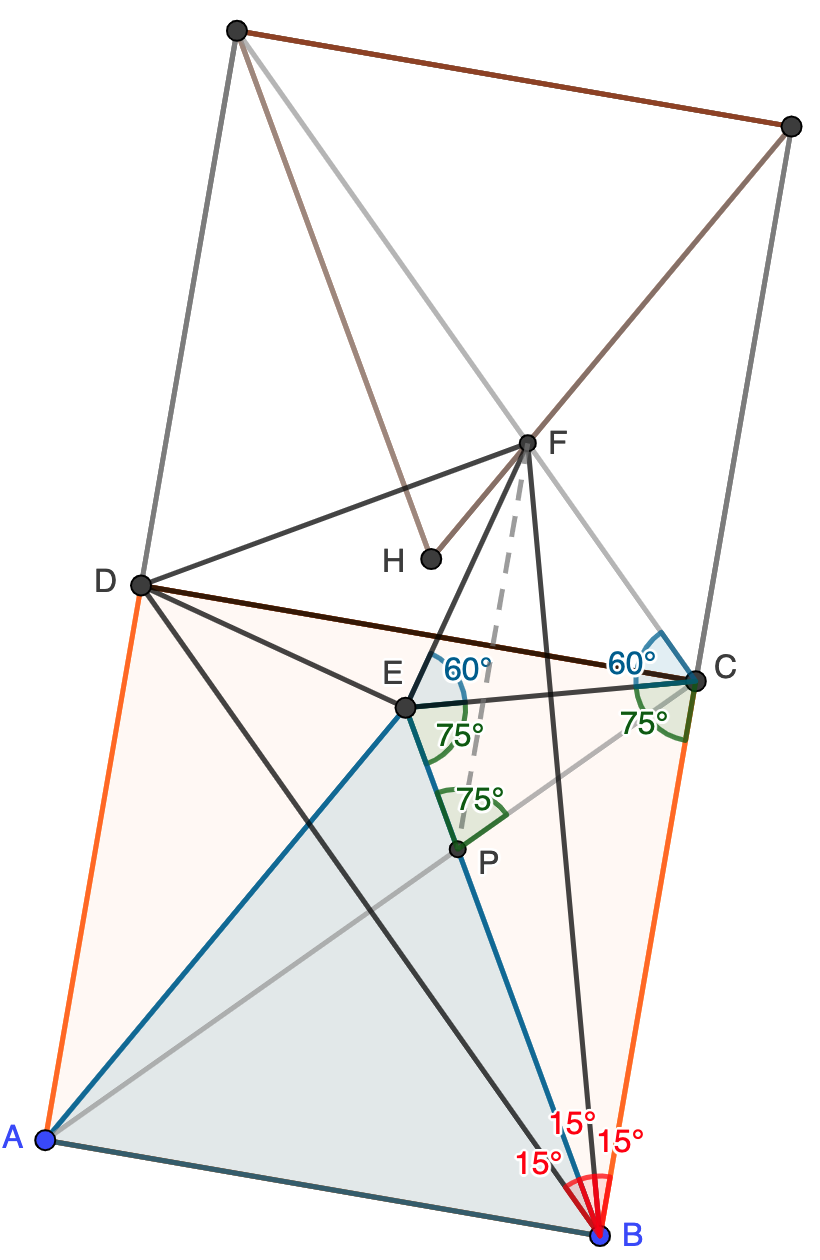
Solución. El triángulo $ECB$ es isósceles ya que tiene dos de sus lados iguales a los lados del cuadrado $ABCD$. Como $\angle EBC=90-60=30$, tenemos que $\angle BEC=\angle ECB=75$ (para que los ángulos de este triángulo sumen $180$). Esto nos dice que $\angle DCE=90-75=15$, con lo que $\angle FCE=15+45=60$. Ahora bien, también tenemos que $\angle EPC=\angle APB=180-\angle PAB-\angle PBA=180-60-45=75$, luego $PCE$ es un triángulo isósceles. Tenemos así que $CP=EC$, pero también tenemos que $CP=CF$ por simetría, luego $CEF$ es equilátero por tener dos lados iguales que forman un ángulo igual a $60$. Hemos respondido así al apartado (a).

Que $CEF$ es equilátero implica que $EF=CE=DE$, ya que $CDE$ es claramente isósceles. Además, esto último nos dice que $\angle DEF=180-15-15=150$, con lo que $\angle DEF=150-60=90$. Tenemos entonces probado el apartado (b): $DEF$ es rectángulo e isósceles porque tiene dos lados iguales que forman un ángulo recto.

Ahora observamos que $\angle DEB=60+75=\angle FEB$, luego la recta $EB$ es la bisectriz interior del ángulo recto $\angle DEF$. Esta bisectriz es mediatriz del triángulo isósceles $DEF$, luego cualquier punto de $BE$ está a la misma distancia de $D$ que de $F$. En particular, el triángulo $BDF$ es isósceles y ya tenemos (c).

Tenemos que $PDF$ es isósceles por el mismo motivo, luego será suficiente ver que $\angle DFP=60$ y habremos terminado (hay realmente muchas formas de hacerlo). Como $\angle DBE=60-45=15$, tenemos que $\angle EBF=15$, luego también tenemos que $\angle FBC=90-45-15-15=15$. En otras palabras, $FB$ es bisectriz (y por tanto mediatriz) en el triángulo isósceles $CBE$, luego también lo es del triángulo equilátero $EFC$. Esto nos lleva a que $\angle EFB=\angle BFE=30$. Si trazamos ahora el segmento $PF$, que es paralelo a $BC$ por la simetría, tenemos que $\angle PFB=\angle CBF=15$ por ser ángulos internos alternos, luego $\angle DFP=45+15=60$ como queríamos probar.