Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Llamemos $\alpha,\beta,\gamma$ a las raíces de $P(x)$, con lo que las raíces de $Q(x)$ son $\frac{1}{\alpha},\frac{1}{\beta},\frac{1}{\gamma}$. Desarrollando e igualando coeficientes en las identidades \begin{align*} P(x)&=(x-\alpha)(x-\beta)(x-\gamma)=x^3+ax^2+bx+c,\\ Q(x)&=(x-\frac{1}{\alpha})(x-\frac{1}{\beta})(x-\frac{1}{\gamma})=x^3+Ax^2+Bx+C, \end{align*} obtenemos las relaciones de Cardano-Vieta para ambos polinomios: \begin{align*} a&=-\alpha-\beta-\gamma&A&=-\frac{1}{\alpha}-\frac{1}{\beta}-\frac{1}{\gamma},\\ b&=\alpha\beta+\beta\gamma+\gamma\alpha&B&=\frac{1}{\alpha\beta}+\frac{1}{\beta\gamma}+\frac{1}{\gamma\alpha}. \end{align*} Ahora utilizamos la desigualdad entre las medias aritmética y armónica y el hecho de que $\alpha,\beta,\gamma\gt 0$ para estimar: \begin{align*} \frac{3}{-A}&=\frac{3}{\frac{1}{\alpha}+\frac{1}{\beta}+\frac{1}{\gamma}}\leq\frac{\alpha+\beta+\gamma}{3}=\frac{-a}{3},\\ \frac{3}{B}&=\frac{3}{\frac{1}{\alpha\beta}+\frac{1}{\beta\gamma}+\frac{1}{\gamma\alpha}}\leq\frac{\alpha\beta+\beta\gamma+\gamma\alpha}{3}=\frac{b}{3}. \end{align*} De aquí se obtienen las desigualdades $aA\geq 9$ y $b\beta\geq 9$ (teniendo en cuenta que $-A\geq 0$ y $B\geq 0$).

Nota. La primera igualdad se alcanza cuando $\alpha=\beta=\gamma$, es decir, cuando los polinomios son cubos perfectos con raíces inversas, esto es, \[P(x)=x^3-3rx^2+3r^2x-r^3,\qquad Q(x)=x^3-\tfrac{3}{r}x^2+\tfrac{3}{r^2}x-\frac{1}{r^3},\] para cierto $r\gt 0$. La segunda igualdad se alcanza cuando $\alpha\beta=\beta\gamma=\gamma\alpha$, que claramente equivale a $\alpha=\beta=\gamma$.

Solución. Vamos a denotar por $p_{X,Y}$ a la probabilidad de que gane el jugador $X$ cuando va a hacer su tirada el jugador $Y$. Observamos que cuando tira un jugador, tiene una probabilidad de ganar directamente $\frac{1}{6}$ y los otros $\frac{5}{6}$ son su probabilidad de ganar una vez le toca al siguiente. De esta forma, tenemos los siguientes tres sistemas de ecuaciones lineales para las nueve probabilidades que desconocemos: \[\left\{\begin{array}{l}p_{A,A}=\frac{1}{6}+\frac{5}{6}p_{A,B}\\p_{A,B}=\frac{5}{6}p_{A,C}\\p_{A,C}=\frac{5}{6}p_{A,A}\end{array}\right.\quad \left\{\begin{array}{l}p_{B,A}=\frac{5}{6}p_{B,B}\\p_{B,B}=\frac{1}{6}+\frac{5}{6}p_{B,C}\\p_{B,C}=\frac{5}{6}p_{B,A}\end{array}\right.\quad \left\{\begin{array}{l}p_{C,A}=\frac{5}{6}p_{C,B}\\p_{C,B}=\frac{5}{6}p_{C,C}\\p_{C,C}=\frac{1}{6}+\frac{5}{6}p_{C,A}\end{array}\right.\] Esto responde al diagrama indicado en la figura más abajo. En realidad, los tres sistemas lineales son el mismo (renombrando las incógnitas) y se pueden resolver fácilmente: \[\left\{\begin{array}{l}p_{A,A}=\frac{36}{91}\\p_{A,B}=\frac{25}{91}\\p_{A,C}=\frac{30}{91}\end{array}\right.\qquad \left\{\begin{array}{l}p_{B,A}=\frac{30}{91}\\p_{B,B}=\frac{36}{91}\\p_{B,C}=\frac{25}{91}\end{array}\right.\qquad \left\{\begin{array}{l}p_{C,A}=\frac{25}{91}\\p_{C,B}=\frac{30}{91}\\p_{C,C}=\frac{36}{91}\end{array}\right.\] Al empezar jugando $A$ la probabilidad que tiene de ganar es $\frac{36}{91}$, mientras que la probabilidad de $B$ es $\frac{30}{91}$ y la de $C$ es $\frac{25}{91}$. Si Carlos apuesta 1€, entonces Blas tiene que apostar $\frac{30}{25}=1.2$€ y Ana tiene que apostar $\frac{36}{25}=1.44$€ (la apuesta tiene que ser proporcional a la probabilidad de ganar si queremos que el juego sea equitativo).

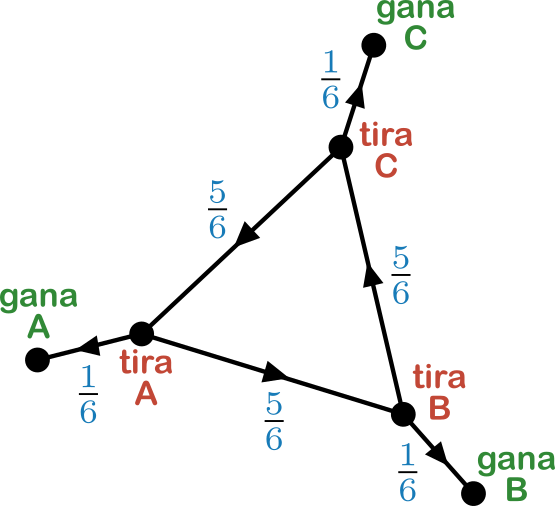
Nota. Este esquema para calcular probabilidades, aunque puede parecer sofisticado, es un método establecido en matemáticas conocido como cadenas de Markov. Si quisiéramos hacer un árbol con todas las posibilidades, sería infinito ya que podría ocurrir que nunca nadie saque un $6$. De esta manera, se entiende mucho mejor la logística del juego.

Solución. Que están en progresión aritmética nos dice que $\log_b(x)=\frac{1}{2}(\log_a(x)+\log_c(x))$. Utilizando que $\log_y(x)$ y $\log_x(y)$ son inversos, podemos expresarlo equivalentemente como \begin{align*} \frac{2}{\log_x(b)}=\frac{1}{\log_x(a)}+\frac{1}{\log_x(c)}&\ \Longleftrightarrow\ \frac{\log_x(b)}{2}=\frac{\log_x(a)\log_x(c)}{\log_x(ac)}\\ &\ \Longleftrightarrow\ \frac{\log_x(b)}{\log_x(a)}=\frac{\log_x(c^2)}{\log_x(ac)}\\ &\ \Longleftrightarrow\ \log_a(b)=\frac{\log_x(c^2)}{\log_x(ac)} \\ &\ \Longleftrightarrow\ \log_a(b)\log_x(ac)=\log_x(c^2) \end{align*} Esto nos dice finalmente que \[c^2=x^{\log_x(c^2)}=x^{\log_a(b)\log_x(ac)}=(x^{\log_x(ac)})^{\log_a(b)}=(ac)^{\log_a(b)}.\]

Solución. Para que los productos sean iguales, es fácil darse cuenta de que si en el tablero hay algún número divisible entre un primo $p$ pero ninguno entre $p^2$, hay un único patrón de casillas donde puede aparece el primo $p$, que están indicadas en la siguiente tabla: \[\begin{bmatrix}p&\cdot&\cdot&\cdot\\ \cdot&\cdot&p&\cdot\\ \cdot&\cdot&\cdot&p\\ \cdot&p&\cdot&\cdot\end{bmatrix}.\] Cuando decimos que es único, debe entenderse salvo rotaciones y simetrías. En este patrón, hay una única casilla marcada con el primo $p$ en cada fila, en cada columna y en cada diagonal principal. Ahora el truco es replicar el patrón con los primos $2,3,5,7,11,13,\ldots$, rotándolo y simetrizándolo para que, al multiplicar los resultados, se cumplan las siguientes dos condiciones:

• Todas las casillas tienen valores distintos.
• Ninguna casilla sobrepasa $99$.

Probando un poco (ver la nota), llegamos a la configuración de la siguiente tabla, lo que da una respuesta afirmativa al problema: \[\begin{bmatrix}2\cdot 3&5&7\cdot 11&13\\ 11&7\cdot 13&2\cdot 5&3\\ 5\cdot 13&3\cdot 11&1&2\cdot 7\\ 7&2&3\cdot 13&5\cdot 11\end{bmatrix}\equiv \begin{bmatrix} 6&5&77&13\\ 11&91&10&3\\ 65&33&1&14\\ 7&2&39&55 \end{bmatrix}\]

Nota. Para conseguir la configuración final, hemos puesto los dos primos menores ($2$ y $3$) en la misma esquina con configuraciones simétricas, los dos siguientes ($5$ y $7$) en la esquina opuesta y $11$ y $13$ en las otras dos esquinas. Al hacer esto, obteníamos en una casilla el número $11\cdot 13$, que se pasaba de $100$, pero hemos podido resolver el problema intercambiando los papeles del $7$ y el $11$.

Solución. Si llamamos $x=BD$ e $y=AD$, tenemos claramente que $x+y=c$ y, por el teorema de la bisectriz, también que $\frac{x}{b}=\frac{y}{c}$. Esto nos da un sistema de dos ecuaciones lineales con dos incógnitas $x$ e $y$, que se resuelve fácilmente, dando \[x=\frac{ac}{a+b},\qquad y=\frac{bc}{a+b}.\] El teorema del seno en los triángulos $ACD$ y $ABC$ nos dice que \[\frac{\mathrm{sen}(\frac{C}{2})}{y}=\frac{\mathrm{sen}(A)}{CD}=\frac{a\,\mathrm{sen}(C)}{c\cdot CD}.\] De aquí podemos despejar \[CD=\frac{ay\,\mathrm{sen}(C)}{c\,\mathrm{sen}(\frac{C}{2})}=\frac{2a\frac{bc}{a+b}\,\mathrm{sen}(\frac{C}{2})\cos(\frac{C}{2})}{c\,\mathrm{sen}(\frac{C}{2})}=\frac{2ab\cos(\frac{C}{2})}{a+b},\] donde hemos usado la fórmula del seno del ángulo doble $\mathrm{sen}(C)=2\mathrm{sen}(\frac{C}{2})\cos(\frac{C}{2})$.