Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. La cara de dimensiones $3^{2003}\times 5^{2003}$ del ortoedro grande tiene un área impar que debería ser rellenada con copias de las caras del ortoedro pequeño. Sin embargo, cada una de las caras del ortoedro pequeño tiene área par, luego el apilamiento es imposible (un número impar no se puede escribir como suma de números pares).

Solución. Pongamos que las raíces del polinomio son $\alpha,\beta,\gamma$, luego podemos expresar \[p(x)=x^3+Bx^2+Cx+D=(x-\alpha)(x-\beta)(x-\gamma).\] Desarrollando e igualando coeficientes, obtenemos las relaciones de Cardano-Vieta para este polinomio. Concretamente, tenemos que \[B=-(\alpha+\beta+\gamma),\quad C=\alpha\beta+\beta\gamma+\alpha\gamma,\quad D=\alpha\beta\gamma.\] Si imponemos la condición del enunciado de que $\alpha\beta=\gamma^2$, podemos entonces calcular \begin{align*} C^3=(\alpha\beta+\beta\gamma+\alpha\gamma)^3&=(\gamma^2+\beta\gamma+\alpha\gamma)^3\\ &=\gamma^3(\alpha+\beta+\gamma)^3=-\alpha\beta\gamma B^3=DB^3. \end{align*}

Solución. Pongamos los puntos $P,Q,R,S$ como se indica en la figura más abajo y también supongamos que el lado del cuadrado es $1$ haciendo una homotecia si fuera necesario (no hay pérdida de generalidad). Vamos a comenzar expresando los lados de $PDE$ en términos de $x$. Como $PE=AP=1-PD$, el teorema de Pitágoras en el triángulo $PDE$ nos dice que $(1-PD)^2=PD^2+x^2$. Por tanto, \[DE=x,\qquad PD=\frac{1-x^2}{2},\qquad PE=1-PD=\frac{1+x^2}{2}.\] Tenemos de esta forma que el triángulo $PDE$ tiene perímetro $x+1$.

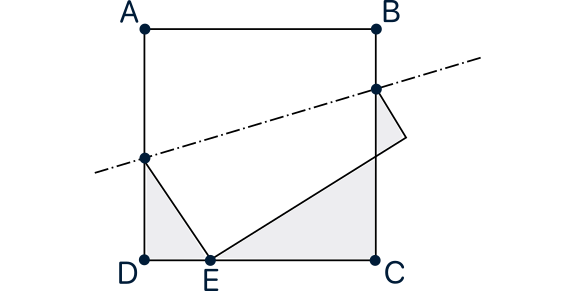
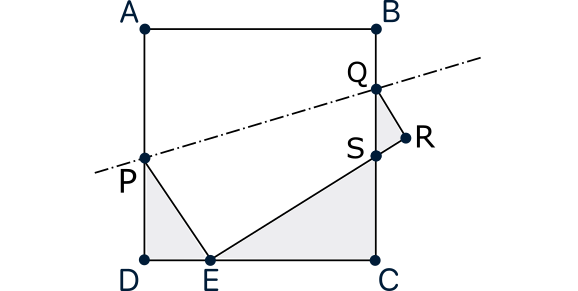
Los triángulos sombreados $PDE$, $SCE$ y $SRQ$ son semejantes (son rectángulos y es muy fácil ver que tienen otro ángulo igual). Como $EC=1-DE=1-x$ se corresponde en la semejanza con $PD= \frac{1-x^2}{2}$, el factor de proporcionalidad para pasar de $PDE$ a $SCE$ es $\frac{2}{1+x}$, luego deducimos que $SCE$ tiene perímetro $2$ (la mitad del perímetro del cuadrado, lo que responde a una de las preguntas del enunciado. Así, las longitudes de los lados de $SCE$ (nos las piden también en el enunciado) son \[CE=\frac{2x}{1+x},\qquad SC=1-x,\qquad SE=\frac{1+x^2}{1+x}.\] Ahora observamos que $SR=1-SE=\frac{x(1-x)}{1+x}$. Como este lado se corresponde con $SC=1-x$ en la semejanza, tenemos que el factor de semejanza para pasar de $SCE$ a $SRQ$ es $\frac{1-x}{2}$, por lo que el perímetro de $SRQ$ es $2\cdot \frac{1-x}{2}=1-x$ y sus lados vienen dados por \[RQ=\frac{x(1-x)}{1+x},\qquad SR=\frac{(1-x)^2}{2},\qquad SQ=\frac{(1+x^2)(1-x)}{2(1+x)}.\] La suma de los perímetros de $PDE$ y $SRQ$ es $(1+x)+(1-x)=2$, el perímetro de $SCE$, luego ya hemos demostrado todo lo que nos piden.

Solución. Expresamos todo en términos del seno y el coseno, teniendo en cuenta las definiciones de las funciones trigonométricas \begin{align*} \mathrm{tg}(x)&=\frac{\mathrm{sen}(x)}{\mathrm{cos}(x)},& \mathrm{cotg}(x)&=\frac{\mathrm{cos}(x)}{\mathrm{sen}(x)},\\ \sec(x)&=\frac{1}{\mathrm{cos}(x)},& \mathrm{cosec}(x)&=\frac{1}{\mathrm{sen}(x)}. \end{align*} Utilizando también la identidad fundamental $\mathrm{sen}^2(x)+\cos^2(x)=1$, podemos transformar la ecuación inicial como sigue: \begin{align*} -3&=\frac{1}{\mathrm{sen}^2(x)}-\frac{1}{\cos^2(x)}-\frac{\mathrm{sen}^2(x)}{\mathrm{cos}^2(x)}-\frac{\mathrm{cos}^2(x)}{\mathrm{sen}^2(x)}-\mathrm{sen}^2(x)-\cos^2(x)\\ &=\frac{\cos^2(x)-\mathrm{sen}^2(x)-\mathrm{sen}^4(x)-\cos^4(x)}{\mathrm{sen}^2(x)\cos^2(x)}-1\\ &=\frac{\cos^2(x)-\mathrm{sen}^2(x)-\mathrm{sen}^2(x)(1-\cos^2(x))-\cos^2(x)(1-\mathrm{sen}^2(x))}{\mathrm{sen}^2(x)\cos^2(x)}-1\\ &=\frac{-2\mathrm{sen}^2(x)+2\mathrm{sen}^2(x)\cos^2(x)}{\mathrm{sen}^2(x)\cos^2(x)}-1=\frac{-2}{\cos^2(x)}+1 \end{align*} Por tanto, podemos escribir finalmente nuestra ecuación como $\cos(x)=\pm\frac{\sqrt{2}}{2}$, lo que nos da las soluciones $x=45$, $x=135$, $x=225$ y $x=315$ en el intervalo $[0,360]$. El resto de soluciones se obtienen sumando a estas un múltiplo entero de $360$.

Si dividimos $2003$ entre $360$, obtenemos cociente $5$ y resto $203$, es decir, $2003^\circ$ consiste en dar 5 vueltas a la circunferencia goniométrica y añadir $203^\circ$, lo que nos da la solución más cercana $5\cdot 360^\circ+225^\circ=2025^\circ$ y esta es la respuesta buscada.

Solución. En un polígono regular de 21 lados hay 10 distancias posibles entre vértices ya que los 20 segmentos que salen de un vértice concreto tienen longitudes iguales por parejas simétricas. Por tanto, si elegimos $n\geq 6$ o más vértices, tendremos $\binom{n}{2}\geq\binom{6}{2}=15$ segmentos entre ellos y la respuesta será negativa. La pregunta es si se puede con 5 vértices, que definen justamente $\binom{5}{2}=10$ segmentos, es decir, ¿existen 5 vértices del 21-ágono regular tales que todas sus distancias son distintas? La respuesta es que sí, como se muestra en la figura.