Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Pongamos $x=AC$ y $r=AO$. Entonces, $CO=r-x$ y el teorema de la altura en el triángulo rectángulo $ADO$ nos dice que $CD^2=AC\cdot CO=x(r-x)$, de donde $AD^2=AC^2+CD^2=x^2+x(r-x)=rx$ por el teorema de Pitágoras. De forma similar, en el triángulo rectángulo $AEO$, el teorema de la altura nos dice que $CE^2=AC\cdot CB=x(2r-x)$, luego
\[AE^2=AC^2+CE^2=x^2+x(2r-x)=2xr=2AD^2,\]
como queríamos probar.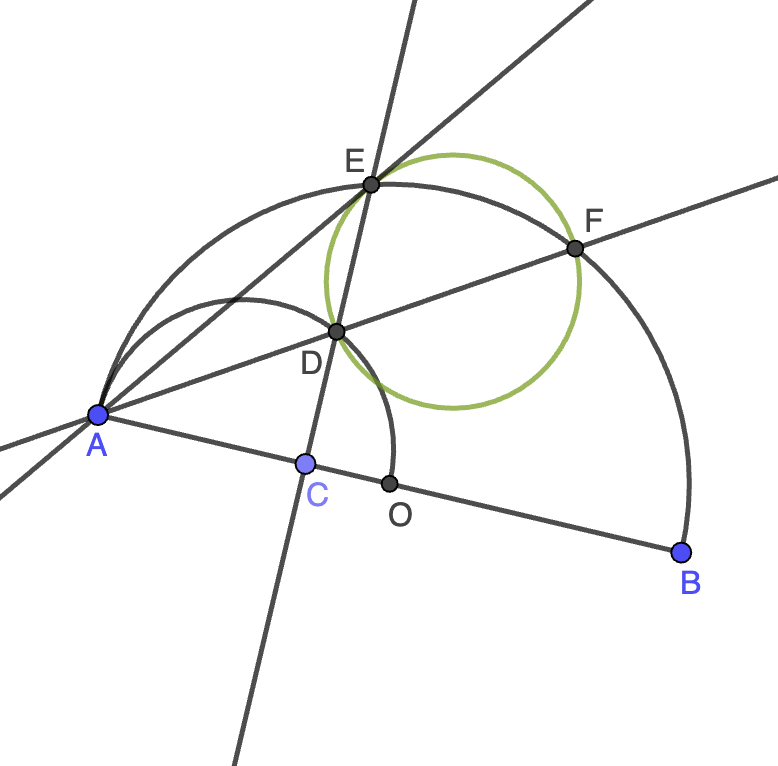
Informar de error en enunciado Informar de procedencia del problema
Nota. El problema también se puede resolver mediante combinaciones con repetición usando separadores. Expresando $x=1+x'$, $y=1+y'$ y $z=1+z'$, tenemos que encontrar la cantidad de ternas $x',y',z'\geq 0$ tales que $x'+y'+z'=36$, lo que equivale a elegir dos separadores en una lista de $36+2=38$ elementos, esto es, el número de soluciones es \[\binom{38}{2}=\frac{38\cdot 37}{2}=703.\]
Informar de error en enunciado Informar de procedencia del problema
Pongamos entonces que tenemos el triángulo equilátero y llamamos a sus vértices $V_1,V_2,V_3$. Cualquier otro de los 6 puntos tendrá la misma distancia a dos de estos vértices por el principio del palomar, luego estará en una de las mediatrices del triángulo equilátero. De hecho, hay exactamente cuatro puntos $V$ de la mediatriz de $V_1V_2$ tales que $\{V_1,V_2,V_3,V\}$ definen solo dos distancias, que están representados en la figura: el punto azul (circuncentro), los puntos rojo y amarillo (a distancia de $V_3$ igual al lado del triángulo equilátero) y el verde (simétrico de $V_3$ respecto de $V_1V_2$). Haciendo lo mismo con las otras mediatrices, tenemos solo 10 posibles puntos de donde elegir los 3 que nos quedan por poner. No es difícil descartar todas las posibilidades, teniendo en cuenta lo siguiente (se deja como ejercicio completar los detalles):
- No puede haber tres puntos alineados (salvo que uno sea el punto medio de los otros dos). Esto descarta que el punto azul pueda ser uno de los 3 puntos restantes.
- Si hay dos puntos del mismo color, entonces estos junto con dos de los vértices $V_1,V_2,V_3$ forman un trapecio y definen al menos tres distancias distintas. Si consideráramos 7 puntos en lugar de 6 ya podríamos terminar aquí porque al no ser el azul uno de ellos, en alguno de los otros dos colores habría al menos dos de los cuatro puntos restantes por el principio del palomar,
- Los tres puntos restantes tendrían que ser entonces un punto verde, otro rojo y otro amarillo, no alineados. Sólo hay una posible elección salvo movimientos rígidos. En este caso también tenemos muchas distancias distintas: el lado del triángulo, la distancia verde-amarillo y la distancia amarillo-vértice.

Nota. El resultado no es cierto con 5 puntos. Por ejemplo, los vértices de un pentágono regular definen 10 segmentos de solamente dos longitudes distintas: la del lado y la de la diagonal.
Informar de error en enunciado Informar de procedencia del problema
Nota. Es interesante preguntarse si realmente es que no se pueden calcular todas las soluciones, pero no es así. Si obviamos las soluciones $(2,2)$ y $(3,3)$ obtenidas, podemos sumar y restar las dos ecuaciones dadas para obtener el sistema cuadrático siguiente (tras simplificar el factor $x-y$ que aparece en la diferencia): \[\left\{\begin{array}{l} 2xy-x-y=7\\ x^2+y^2-5x-5y=-12 \end{array}\right.\] Despejando $x=\frac{7+y}{2y-1}$ en la primera ecuación y sustituyendo en la segunda, obtenemos la ecuación cuadrática $y^4-6 y^3+15 y^2-26 y+24=0$, cuyas únicas soluciones reales son $y=2$ e $y=3$ (se obtienen por Ruffini). Por tanto, el sistema del enunciado tiene cuatro soluciones: $(2,2)$, $(3,3)$, $(2,3)$ y $(3,2)$.
Informar de error en enunciado Informar de procedencia del problema
El teorema de Pitágoras en $ABH$ y $ACH$ nos da $8^2-CH^2=AH^2=11^2-BH^2$, luego \[(BH+CH)(BH-CH)=BH^2-CH^2=11^2-8^2=57.\] Como $BH+CH=a=\frac{38}{3}$, obtenemos que $BH-CH=57/\frac{38}{3}=\frac{9}{2}$. Esta ecuación junto con $BH+CH=\frac{38}{3}$ nos da un sistema lineal cuya solución es $BH=\frac{103}{12}$ y $CH=\frac{49}{12}$. Por otro lado, podemos calcular $CD=\frac{a}{2}-1=\frac{16}{3}$. Finalmente, todo esto nos dice que $DH=CD-CH=\frac{16}{3}-\frac{49}{12}=\frac{5}{4}$.

Informar de error en enunciado Informar de procedencia del problema