Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 669
OIM, 1993-P3
Hallar todas las funciones $f:\mathbb{N}\to\mathbb{N}$ que cumplen simultáneamente las siguientes dos condiciones:
- Si $x\lt y$, entonces $f(x)\lt f(y)$.
- $f(yf(x))= x^2 f(xy)$ para cualesquiera $x,y\in\mathbb{N}$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 668
OIM, 1993-P2
Demostrar que, para cualquier polígono convexo de área $1$, existe un paralelogramo de área $2$ que lo contiene.
pistasolución 1info
Pista. Toma el menor paralelogramo que contiene al polígono y con uno de sus lados paralelo al segmento que une los dos vértices más distantes.
Solución. Sean $A$ y $B$ los dos vértices más alejados entre sí del polígono y consideramos los dos vértices $C$ y $D$ más alejados de la recta $AB$ en sendos semiespacios definidos por $AB$. Trazamos por $A$ y $B$ perpendiculares $r_A$ y $r_B$ a $AB$ y por $C$ y $D$ paralelas $r_C$ y $r_D$ a $AB$. Estas cuatro rectas $r_A,r_B,r_C,r_D$ determinan un rectángulo $R$. Vamos a ver que $R$ (que es, en particular, paralelogramo) contiene al polígono y que tiene área menor o igual que $2$.
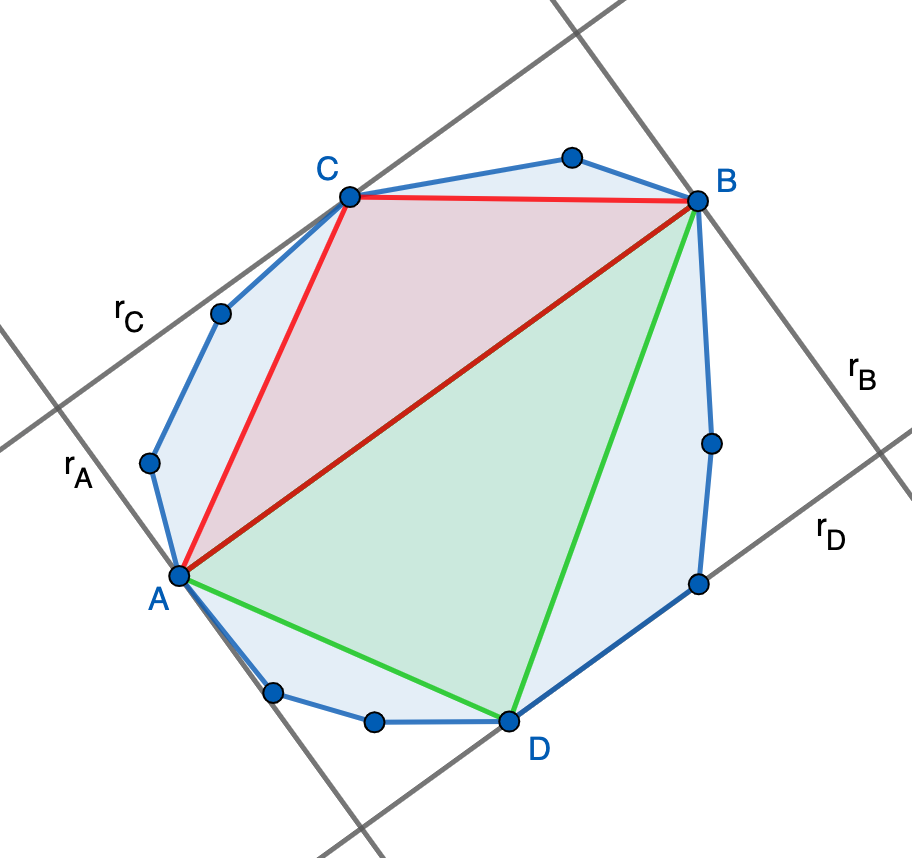
- En primer lugar, tenemos que ningún vértice se puede salir de la banda determinada por $r_A$ y $r_B$ ya que en tal caso dicho vértice tendría distancia con $A$ o con $B$ mayor que $AB$ (¿por qué?), contradiciendo que $AB$ es el segmento entre vértices de longitud máxima. Por otro lado, ningún vértice se puede salir de la banda determinada por $r_C$ y $r_D$ ya que en tal caso dicho vértice distaría de $AB$ más que $C$ o $D$, contradiciendo que estos son los puntos más alejados. Por tanto, todos los vértices del polígono están en $R$ y, por convexidad, todo el polígono debe estar en $R$.
- Finalmente, veamos que $\text{área}(R)\leq 2$. Para ello, observamos que los triángulos $ACB$ y $ADB$ están contenidos en el polígono (de nuevo, por convexidad), de donde \[1=\text{área}(\text{polígono})\geq\text{área}(ACB)+\text{área}(ADB)=\tfrac{1}{2}\text{área}(R).\]
Esto termina la demostración. Es importante observar que uno de los dos puntos $C$ o $D$ podría no estar definido porque no haya vértices a un lado de la recta $AB$. En tal caso, se razona de forma similar usando que $r_C=AB$ o $r_D=AB$.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 667
OIM, 1993-P1
Un número natural es capicúa si al escribirlo en el sistema decimal se puede leer de igual forma de izquierda a derecha que de derecha a izquierda. Por ejemplo, $8$, $23432$ y $6446$ son capicúas. Sean $x_1\lt x_2 \lt\ldots\lt x_i\lt x_{i+1}\lt\ldots$ todos los números capicúas ordenados de menor a mayor. ¿Cuántos números primos distintos se pueden expresar como $x_{i+1}-x_i$ para algún $i$?
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 666
OIM, 1992-P5
Sea $\Gamma$ una circunferencia y sean $h$ y $m$ números positivos tales que existe un trapecio $ABCD$ inscrito en $\Gamma$ de altura $h$ y tal que la suma de las bases $AB+CD$ es $m$. Construir el trapecio $ABCD$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 665
OIM, 1992-P3
En un triángulo equilátero $ABC$ cuyo lado tiene longitud $2$, se inscribe una circunferencia $\Gamma$.
- Demostrar que para cada punto $P$ de $\Gamma$, la suma de los cuadrados de sus distancias a los vértices $A$, $B$ y $C$ es $5$.
- Demostrar que para todo punto $P$ de $\Gamma$ es posible construir un triángulo cuyos lados tienen las longitudes de los segmentos $AP$, $BP$ y $CP$ y cuya área es $\frac{\sqrt{3}}{4}$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre