Olimpiadas de Matemáticas
Página de preparación y problemas

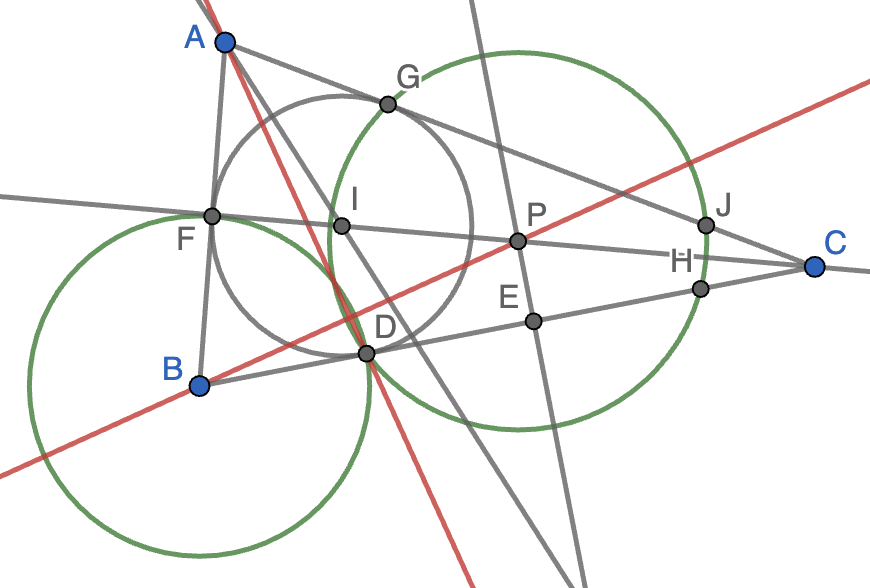
Solución. Sean $F$ y $G$ los puntos en que la circunferencia inscrita es tangente a los lados $AB$ y $AC$, respectivamente. Como $P$ está en la bisectriz $CI$, está a la misma distancia de $G$ y de $D$, luego hay una circunferencia de centro $P$ que pasa por $G$ y $D$, que corta de nuevo a los lados $BC$ y $AC$ en puntos $H$ y $J$, respectivamente, como se muestra en la figura. También está claro que hay una circunferencia de centro $B$ que pasa por $D$ y $F$. Vamos a ver que $AD$ es el eje radical de ambas circunferencias, luego será perpendicular a $BP$, la recta que une sus centros.

Para ver esto, será suficiente ver que $A$ tiene la misma potencia respecto de ambas circunferencias. La potencia de $A$ respecto de la circunferencia de centro $B$ es $AF\cdot(AF+2BF)$. La potencia de $A$ respecto de la circunferencia de centro $P$ es $AG\cdot AJ$. Ahora bien, tenemos que $AG=AF$ por estar $A$ en la bisectriz del ángulo $A$ y $GJ=DH$ por estar $P$ en la bisectriz del ángulo $C$. Además, $DH=2DE$ por ser $E$ el pie de la perpendicular a la cuerda $DH$ desde el centro $P$ y, finalmente, $DE=BD$ por la hipótesis del enunciado. Tenemos así que $AG\cdot AJ=AF\cdot(AF+2BF)$, como queríamos demostrar.

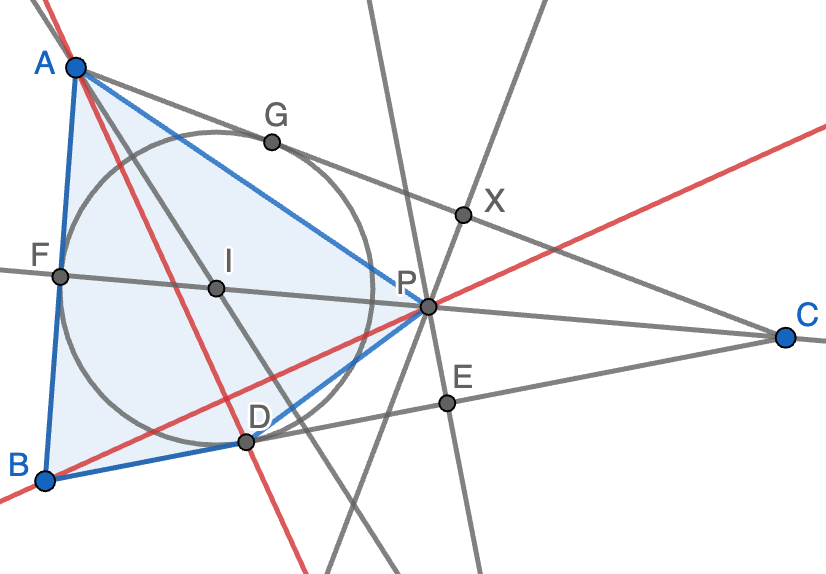
Solución. Vamos a probar que $AB^2+DP^2=AP^2+BD^2$, lo que implica que las dos diagonales del cuadrilátero $ABDP$ (sombreado en azul) son perpendiculares y se tiene el resultado deseado. Sea $X$ el pie de la perpendicular por $P$ al lado $AC$. Usando que $PX=PE$ y $BD=BE$, así como el teorema de Pitágoras en los triángulos rectángulos $AXP$ y $DPE$, tenemos que \[AB^2+DP^2=AB^2+DE^2+PE^2=AB^2+BD^2+PX^2=BD^2+AP^2+AB^2-AX^2,\] luego será suficiente con probar que $AB=AX$.

Para ello, sean $F$ y $G$ los puntos en que la circunferencia inscrita es tangente a los lados $AB$ y $AC$, respectivamente. Usando que $CX=CE$, $BF=BD=DE$, $AF=AG$ y $CG=CD$, tenemos que \[AX=AC-CX=AG+CG-CE=AF+CG-CD-BD+2BD=AF+BF=AB.\]

Solución. Hay que probar dos implicaciones. La más sencilla consiste en suponer que $a=b=c$, en cuyo caso para cualquier $x\in\mathbb{R}$ se cumple que \[p(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)=3(x-a)^2\geq 0.\] Recíprocamente, supongamos que $p(x)\geq 0$ para todo $x\in\mathbb{R}$. Podemos simplificar el polinomio operando todos los paréntesis y luego completar cuadrados para obtener que \begin{align*} p(x)&=x^2-ax-bx+ab+x^2-bx-cx+bc+x^2-cx-ax+ca\\ &=3x^2-2(a+b+c)x+(ab+bc+ca)\\ &=3\left(x^2-\tfrac{1}{3}(a+b+c)\right)^2-\tfrac{1}{3}(a+b+c)^2+(ab+bc+ca). \end{align*} Por tanto, este polinomio toma su mínimo valor en $x=\frac{1}{3}(a+b+c)$ y esto nos dice que $p(\frac{1}{3}(a+b+c))\geq 0$. De esta manera \begin{align*} 0\leq 3\, p(\tfrac{1}{3}(a+b+c))&=-(a+b+c)^2+3(ab+bc+ca)\\ &=-(a^2+b^2+c^2)-2(ab+bc+ac)+3(ab+bc+ca)\\ &=-(a^2+b^2+c^2)+(ab+bc+ac)\\ &=-(a-b)^2-(b-c)^2-(c-a)^2. \end{align*} La única forma de que se cumpla esta desigualdad es que $a-b=b-c=c-a=0$, es decir, que $a=b=c$, como queríamos demostrar.

Solución. La idea clave es darse cuenta de que la segunda ecuación se puede escribir equivalentemente como $(x-y)(y-z)(x-z)=0$, lo que nos dice que dos de las incógnitas tienen que ser iguales. Como no hay simetría, tendremos que distinguir tres casos:

• Si $x=y$, entonces la primera ecuación nos dice que $2x+z=1$. Sustituyendo $y=x$ y $z=1-2x$ en la tercera y simplificando, llegamos a la ecuación $3x^2-x=0$, que nos da soluciones $x=0$ y $x=\frac{1}{3}$. Deshaciendo las sustituciones, obtenemos la soluciones al sistema original $(x,y,z)=(0,0,1)$ y $(x,y,z)=(\frac{1}{3},\frac{1}{3},\frac{1}{3})$.
• Si $y=z$, la primera ecuación nos da $x+2y=1$, luego podemos sustituir $z=y$ y $x=1-2y$ en la tercera ecuación y después de simplificar nos queda $y(3y^2-4y+1)=0$, que tiene soluciones $y=0$, $y=1$ e $y=\frac{1}{3}$. En el sistema original, esto se corresponde con las soluciones $(1,0,0)$, $(-1,1,1)$ y $(\frac{1}{3},\frac{1}{3},\frac{1}{3})$, aunque esta última ya la hemos obtenido previamente.
• Si $z=x$, procedemos de forma análoga usando la primera ecuación para obtener $y=1-2x$. Sustituyendo en la tercera y simplificando, llegamos a que $x(9x^2-9x+2)=0$, ecuación que tiene por soluciones $x=0$, $x=\frac{1}{3}$ y $x=\frac{2}{3}$. Estas nos dan las soluciones del sistema $(0,1,0)$, $(\frac{1}{3},\frac{1}{3},\frac{1}{3})$ y $(\frac{2}{3},\frac{-1}{3},\frac{2}{3})$.

Se han obtenido así un total de $7$ soluciones distintas.