Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 460
Dados cuatro puntos en el interior o en el borde de un cuadrado de lado $1$, demostrar que al menos dos de ellos están a una distancia menor o igual que $1$.
pistasolución 1info
Pista. Busca ángulos obtusos formados por los puntos, Si no se cumple el enunciado, entonces esto te llevará a distancias mayores que la de la diagonal del cuadrado, lo cual es imposible.
Solución. Sean $A,B,C$ puntos tales que $\angle ABC>90$ y tal que las distancias entre ellos son mayores que $1$. Entonces, el teorema del coseno nos dice que
\[AC^2=AB^2+BC^2-2AB\cdot BC\cos\angle ABC\gt AB^2+BC^2\gt 2,\]
por lo que los puntos $A$ y $C$ están a distancia mayor que $\sqrt{2}$, lo cual es imposible en un cuadrado de lado $1$ (el segmento más largo contenido en él es la diagonal, ¿sabrías probarlo?).
Teniendo esto en cuenta, razonemos por reducción al absurdo suponiendo que todas las distancias entre los cuatro puntos dados son mayores que $1$. El problema se reduce, por tanto, a encontrar tres de los puntos que formen un ángulo obtuso. Distingamos dos casos:
- Si los cuatro puntos son los vértices de un cuadrilátero convexo, entonces no puede ser un cuadrado (porque no puede haber un cuadrado de lado mayor que $1$ contenido en otro de lado $1$). Como los cuatro ángulos del cuadrilátero suman $360º$, al menos uno de ellos será mayor que $90º$ y hemos terminado.
- Si no forman un cuadrilátero convexo, entonces uno de ellos estará dentro del triángulo que forman los otros tres, luego forma con cada par de ellos tres ángulos que suman $360º$ y, al menos uno de ellos será mayor o igual que $120º$, luego mayor que $90º$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 459
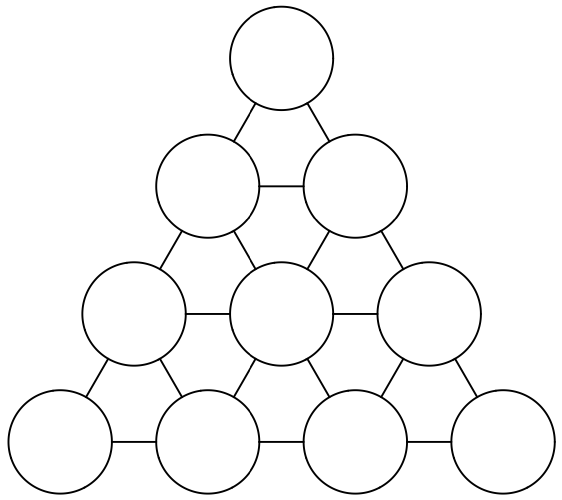
Sobre un tablero en forma de triángulo equilátero con un número par de filas $n$ (tal como se indica en la figura para $n=4$), se juega un solitario. Sobre cada casilla se coloca una ficha. Cada ficha es blanca por un lado y negra por el otro. Inicialmente, sólo una ficha, que está situada en un vértice, tiene la cara negra hacia arriba; las demás fichas tienen la cara blanca hacia arriba. En cada movimiento del juego se retira solamente una ficha negra del tablero y se da la vuelta a cada una de las fichas que ocupa una casilla vecina. Después de varios movimientos, ¿será posible quitar todas las fichas del tablero?
pistasolución 1info
Pista. Cada ficha es vecina de un número par de fichas.
Solución. Cada casilla es vecina de un número par de fichas (las del interior tienen 6 vecinas, las de los lados tienen 4 y las de los vértices tienen 2). Por tanto, si una ficha concreta resulta ser la última en retirarse, antes hemos tenido que quitar todas sus vecinas, lo que supone un número par de cambios de color. Esto nos dice que al proceder a retirar la última, su color es blanco y no puede retirarse. La respuesta a la pregunta del enunciado es, por tanto, negativa.
Nota. ¿Se pueden retirar todas las fichas menos una?
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 458
Demostrar que la siguiente suma
\[\sqrt[3]{\frac{a+1}{2}+\frac{a+3}{6}\sqrt{\frac{4a+3}{3}}}+\sqrt[3]{\frac{a+1}{2}-\frac{a+3}{6}\sqrt{\frac{4a+3}{3}}}\]
no depende del valor de $a\geq\frac{-3}{4}$ y calcular su valor.
pistasolución 1info
Pista. Encuentra una ecuación de tercer grado de la que la expresión del enunciado es solución.
Solución. La condición $a\geq\frac{-3}{4}$ asegura que las raíces cuadradas están bien definidas, luego toda la expresión está bien definida (las raíces cúbicas se pueden calcular para todo número real). Si llamamos $x$ e $y$ a los dos sumandos, no es difícil comprobar que
\[x^3+y^3=a+1,\qquad xy=\frac{-a}{3},\]
por lo que podemos escribir, usando el binomio de Newton,
\[(x+y)^3=x^3+y^3+3xy(x+y)=a+1-a(x+y).\]
En otras palabras, el número del enunciado es solución de la ecuación $z^3+az-a-1=0$. Esta ecuación de tercer grado se puede factorizar como $(z-1)(z^2+z+a+1)=0$ y la ecuación $z^2+z+a+1$ tiene discriminante $1-4(a+1)=-3-4a\leq 0$, siendo la igualdad únicamente para $a=\frac{-3}{4}$. Deducimos que $x+y=1$ para $a\neq\frac{-3}{4}$. Para $a=\frac{-3}{4}$, sustituimos en la expresión del enunciado y obtenemos también que $x+y=1$. Queda así demostrado que dicha expresión es igual a $1$ para todo $a\geq\frac{-3}{4}$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 457
Se llama parte entera de un número real $a$ al mayor número entero menor o igual que $a$. Si $n$ es un número natural, demostrar que la parte entera de $(4+\sqrt{11})^n$ es un número impar.
pistasolución 1info
Pista. Observa que $(4+\sqrt{11})^n+(4-\sqrt{11})^n$ es un entero par.
Solución. Consideremos el número
\[a_n=(4+\sqrt{11})^n+(4-\sqrt{11})^n.\]
Desarrollando por el binomio de Newton, tenemos que
\[a_n=\sum_{k=0}^n\binom{n}{k}4^{n-k}11^{k/2}(1+(-1)^k),\]
luego todos los términos en que $k$ es impar se anulan y el resto queda duplicado. Esto nos dice que $a_n$ es un número par para todo $n\in\mathbb{N}$. Otra forma de ver esto es comprobar que se cumple la relación $a_n=8a_{n-1}+5a_{n-2}$ y, como $a_0=2$ y $a_1=8$ son pares, se sigue que todos los $a_n$ son pares. Ahora bien, se cumple que $4-\sqrt{11}\approx 0.683375$, luego $(4-\sqrt{11})^n$ está entre $0$ y $1$ para todo $n\in\mathbb{N}$. En consecuencia, $(4+\sqrt{11})^n$ es igual al número par $a_n$ menos un número entre $0$ y $1$, luego su parte entera es impar.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 456
Dado un número natural $n\in\mathbb{N}$, demostrar que $1989^n$ se puede escribir como suma de dos cuadrados de enteros positivos como mínimo de dos formas diferentes.
pistasolución 1info
Pista. Observa la identidad $(a^2+b^2)(c^2+d^2)=(ac-bd)^2+(ad+bc)^2$.
Solución. Para $n=1$, tenemos que $1989=9\cdot 221= 3^2(10^2+11^2)=3^2(5^2+14^2)$. Para $n=2$, tenemos que
\[1989^2=9^2\cdot 221^2= 9^2\cdot 48841=9^2(85^2+204^2)=9^2(104^2+195^2).\]
De aquí el resultado es inmediato ya que basta multiplicar uno de estos dos números por el cuadrado perfecto $1989^{2n}=(1989^n)^2$ para obtener cualquier potencia de $1989$. Obviamente, los dos resultados obtenidos de las descomposiciones anteriores son distintos.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre