Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Fijado $k\in\mathbb{N}$, tenemos que $1=x_1\lt x_2\lt\ldots\lt x_{k+1}\leq 2k$. Por tanto, $x_1,x_2,\ldots x_{k+1}$ son $k+1$ elementos distintos de $[1,2k]\cap\Z$. Como este conjunto se descompone como unión de los $k$ subconjuntos $\{1,k+1\},\{2,k+2\},\ldots,\{k,2k\}$, el principio del palomar nos dice que uno de estos subconjuntos debe contener a dos de los números $x_1,x_2,\ldots x_{k+1}$. Estos dos elementos de la sucesión se diferencian en $k$ unidades y hemos terminado.

Solución. Para probar la primera desigualdad, vamos a aplicar la desigualdad entre las medias aritmética y geométrica a los números $x_1=x_2=\ldots=x_n=\frac{1}{n}$ y $x_{n+1}=\frac{1}{n+1}$. Como no todos estos números son iguales, tendremos una desigualdad estricta: \begin{align*} \sqrt[n+1]{\frac{1}{n}\cdots\frac{1}{n}\cdot\frac{1}{n+1}}\lt \frac{\frac{1}{n}+\ldots+\frac{1}{n}+\frac{1}{n+1}}{n+1}&\Longleftrightarrow \sqrt[n+1]{\frac{1}{n^n(n+1)}}\lt \frac{1+\frac{1}{n+1}}{n+1}\\ &\Longleftrightarrow \frac{1}{n^n(n+1)}\lt \frac{1}{(n+1)^{n+1}}\left(1+\frac{1}{n+1}\right)^{n+1}\\ &\Longleftrightarrow \left(\frac{n+1}{n}\right)^n\lt\left(1+\frac{1}{n+1}\right)^{n+1}, \end{align*} que es la desgiualdad que buscamos.

En cuanto a la segunda desigualdad, desarrollamos por el binomio de Newton \begin{align*} \left(1+\frac{1}{n+1}\right)^{n+1}&=\sum_{k=0}^{n+1}\binom{n+1}{k}\frac{1}{(n+1)^k}=2+\sum_{k=2}^{n+1}\frac{(n+1)n\cdots(n-k+2)}{k!(n+1)^k}\\ &\leq 2+\sum_{k=2}^{n+1}\frac{1}{k!}\leq 2+\sum_{k=2}^{n+1}\frac{1}{k(k-1)}\\ &\leq 2+\sum_{k=2}^{n+1}\left(\frac{1}{k-1}-\frac{1}{k}\right)=3-\frac{1}{n+1}\lt 3. \end{align*} En primer lugar, hemos usado que cada uno de los factores en $(n+1)n\cdots(n-k+2)$ es menor o igual que $n+1$. Después hemos despreciado todos los factores de $k!$ salvo los dos primeros. Finalmente, hemos expresado la suma como una suma telescópica para poder obtener su valor explícito.

Solución. Para cada $i$ entre $1$ y $n$, consideremos la circunferencia $\Gamma_i$ de centro $P_i$ y radio $|r_i|$. No puede haber dos de los $r_i$ que sean negativos o cero ya que entonces tendríamos una distancia negativa o cero (los puntos deben ser distintos). Distinguimos casos:

• Si todos los $r_i$ son positivos, entonces las circunferencias $\Gamma_1,\ldots,\Gamma_n$ son tangentes exteriores dos a dos. Es bien conocido que el número máximo de circunferencias mutuamente tangentes es cuatro (ver la nota), lo que nos da $n\leq 4$ en este caso.
• Si existe un $r_i$ cero y el resto son positivos, pongamos $r_1=0$, entonces las circunferencias $\Gamma_2,\ldots,\Gamma_n$ son mutuamente tangentes exteriormente y además $P_1$ pertenece a todas ellas. Como los puntos de tangencia de $\Gamma_2,\ldots,\Gamma_n$ son distintos, el punto $P_i$ no puede pertenecer a todas las circunferencias salvo que $n=3$. Esto nos dice que $n\leq 3$ en este caso.
• Si existe un $r_i$ negativo y el resto son positivos, pongamos $r_1\lt 0$, entonces las circunferencias $\Gamma_2,\ldots,\Gamma_n$ son mutuamente tangentes exteriormente, mientras que $\Gamma_1$ es tangente interior a todas las demás (siendo $r_1+r_i\gt 0$, se tiene que $|r_1|\leq |r_i|$ para todo $i$). Esto nos dice que $n\geq 2$ en este caso ya que $\Gamma_1$ no puede ser interior a dos o más circunferencias tangentes exteriormente.

Hemos probado así que el máximo buscado es $n=4$.

Nota. El hecho de que el máximo número de circunferencias mutuamente tangentes es cuatro es consecuencia, por ejemplo, del teorema de los círculos de Descartes (aunque puede razonarse independientemente de forma más elemental).

Solución. Está claro que no pueden sentarse más de $n^2$ personas cumpliendo esta condición, ya que en tal caso habría al menos $n+1$ de algún país por el principio del palomar y alguna de las personas a su lado tendría que ser del mismo país ya que sólo hay $n$ países (de nuevo por el principio del palomar. Vamos a ver que efectivamente pueden sentarse $n^2$ personas cumpliendo la propiedad, luego este será el máximo.

Vamos a encontrar la forma de sentarse por inducción sobre $n$. Para el caso base $n=2$, la forma de sentarse es 1221 (cíclicamente), siendo 1 un representante del primer país y 2 un representante del segundo. Ahora bien, para añadir un tercer país añadimos 33231 al inicio de la cadena, para añadir un cuarto país añadimos 4434241, para añadir un quinto país añadimos 554535251 y así sucesivamente, obteniendo las cadenas cíclicas \begin{align*} 1221,\\ 332311221,\\ 4434241332311221,\\ 5545352514434241332311221,\ldots \end{align*} En el paso $n$ se añade la cadena $nn(n-1)n(n-2)\ldots n1$ formada por $2n-1$ números. Como la suma de los impares entre $1$ y $2n-1$ es $n^2$, deducimos que tenemos así $n^2$ números para $n$ países. Ahora bien, cada número $k\lt n$ tiene a su derecha a cada uno de los números entre $1$ y $n-1$ una única vez por hipótesis de inducción y una vez al $n$ en la cadena añadida en el paso $n$. Por su parte, el número $n$ tiene a su derecha una vez a cada uno de los números entre $1$ y $n$ en la cadena añadida en el paso $n$. Por lo tanto, hemos probado que el número máximo es $n^2$.

Solución. La desigualdad de Jensen con pesos $x,y\geq 0$ tales que $x+y=1$, nos dice que si $f:\mathbb{R}\to\mathbb{R}$ es una función estrictamente convexa, entonces \[f(ax+by)\leq xf(a)+yf(b).\] ya que, en el intervalo $[a,b]$, la gráfica de la función se queda por debajo del segmento de recta que une los puntos $(a,f(a)$ y $(b,f(b))$. Ahora bien, fuera del intervalo $[a,b]$, la gráfica se queda por encima de la recta, lo que nos dice que, para $x,y\in\mathbb{R}$ tales que $x+y=1$, si uno de estos dos números es negativo, se cumple la desigualdad contraria: \[f(ax+by)\gt xf(a)+yf(b).\] Por ser un poco más explícitos en este punto, basta mirar la figura y tener en cuenta que:

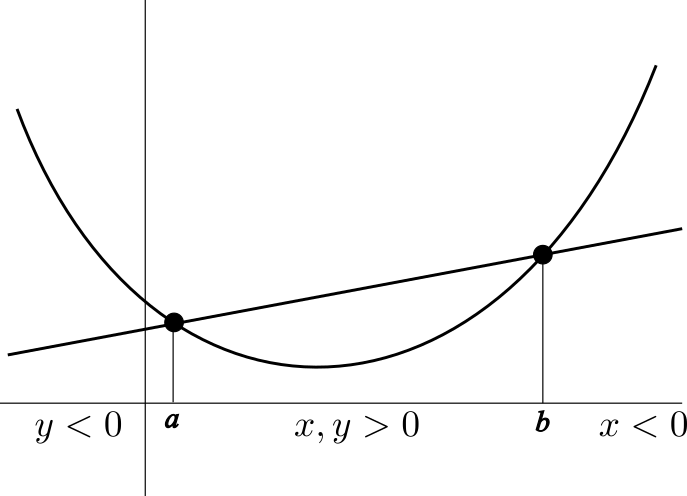
• Si $x+y=1$ y $a\lt b$, entonces el número $ax+by$ está entre $a$ y $b$ para $x,y\geq 0$, a la derecha de $b$ para $x\lt 0$ y a la izquierda de $a$ para $y\lt 0$.
• $f(ax+by)$ es el valor de la función en $ax+by$.
• $xf(a)+yf(b)$ es el valor de la recta en $ax+by$.

Aplicando este razonamiento a las funciones $f(t)=t^2$ y $f(t)=t^4$, que son ambas estrictamente convexas, deducimos que el conjunto de soluciones son los puntos $(x,y)$ que cumplen $x,y\geq 0$ y $x+y=1$. En otras palabras, son los puntos del segmento que une $(1,0)$ y $(0,1)$ en el plano.