Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Observemos que en la figura se forman tres pentagonos y dos cuadrados. Evidentemente, nuestra curva tendría que empezar fuera de (al menos) dos de los pentágonos. Cada vez que la curva atraviesa un lado de uno de estos pentágonos pasará de estar en el interior a estar en el exterior o del exterior al interior. Por tanto, como cada pentágono tiene un número impar de lados, la curva debería terminar en el interior de dos de los pentágonos, lo cual es absurdo. Concluimos que no existe dicha curva.

Solución. Esta es una solución muy estándar usando algo de teoría de grafos. La figura del enunciado es un grafo plano y podemos considerar el grafo dual, que tiene un vértice por cada cara del grafo original y en el que dos vértices se unen por una arista cuando representan a caras adyacentes (ver figura).

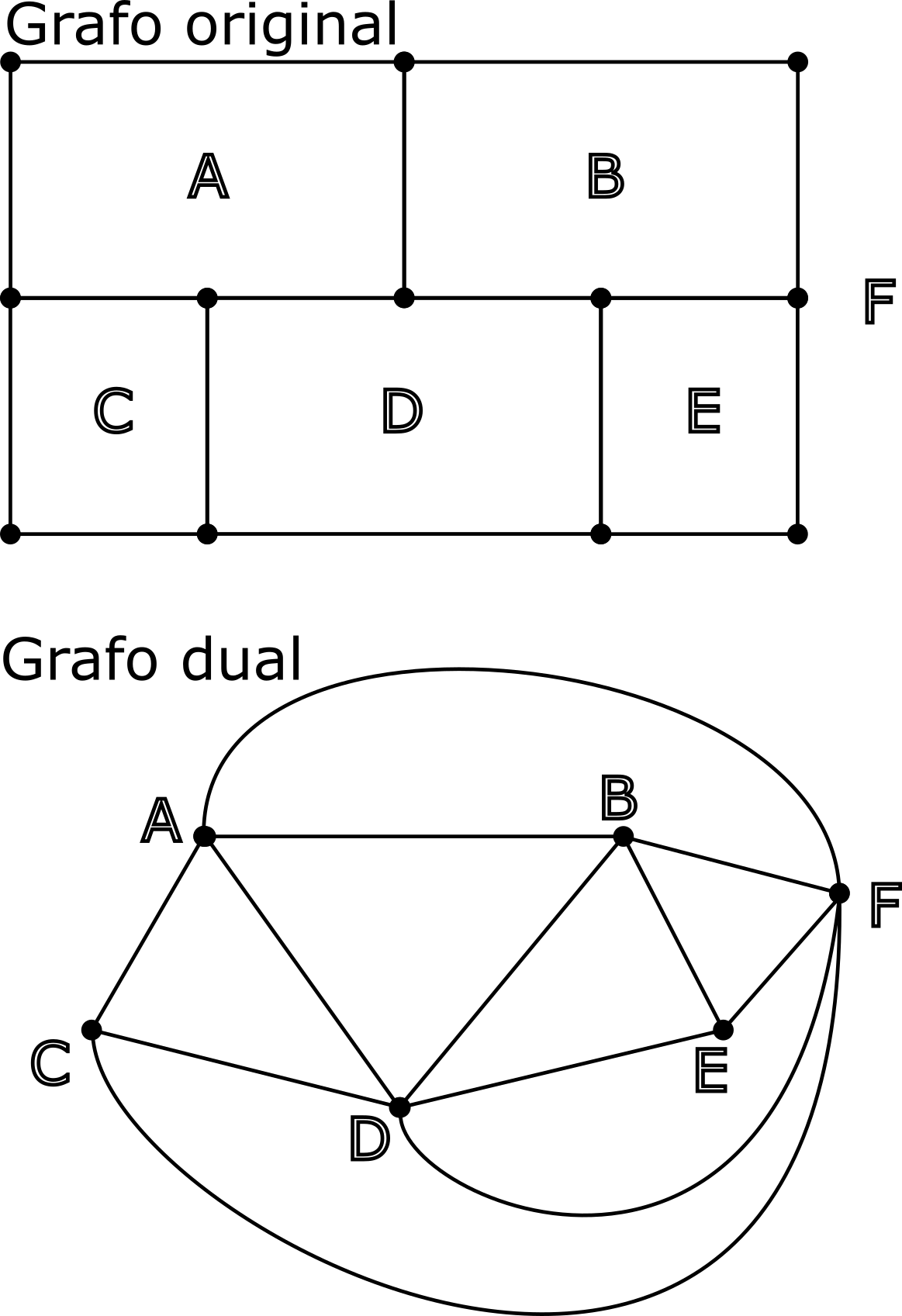
Atravesar una arista del grafo original equivale a recorrer una arista del grafo dual, por lo que el problema se reduce a encontrar un camino que pase por todas las aristas del grafo dual una sola vez. Esto no puede hacerse ya que eso implicaría que hay como máximo dos vértices del grafo dual a los que llegan un número par de aristas (Teorema de Euler). Sin embargo, el grafo dual tiene 4 vértices (C, D, E y F) a los que llegan un número par de aristas, por lo que concluimos que la curva buscada no puede existir.

Solución. Una vez se han elegido los 999 primeros números, su suma tendrá un cierto resto $r$ módulo $n$. Como el último número recorre todos los restos módulo $n$, habrá $1$ posibilidad entre $n$ de que el resto sea $n-r$ y esto no depende de $r$. En otras palabras, la probabilidad sólo depende de la elección del último número y es igual a $\frac{1}{n}$.

Solución. Dado que $a\gt 0$ y el polinomio tiene dos raíces reales, el hecho de que ambas raíces tengan valor absoluto menor que $1$ (es decir, que estén en el intervalo $[-1,1]$) es lo mismo que decir que $p(-1)\geq 0$ y $p(1)\geq 0$ y además que el vértice de la parábola ocurra en un punto del intervalo $[-1,1]$. Las dos primeras condiciones nos dan \begin{align*} p(-1)=a-b+c\geq 0\ &\Leftrightarrow\ a+c\geq b,\\ p(1)=a+b+c\geq 0\ &\Leftrightarrow\ a+c\geq -b, \end{align*} que pueden expresarse conjuntamente como $a+c\geq |b|$. Por otro lado, la parábola tiene su vértice en $x=\frac{-b}{2a}$, luego la tercera condición se traduce en que $|\frac{-b}{2a}|\leq 1$. Elevando al cuadrado, esta condición equivale a que $b^2\leq 4a^2$. Con todo esto en mente, veamos el si y sólo si que se plantea en el enunciado:

• Si las dos raíces tienen valor absoluto menor o igual que $1$, acabamos de ver que debe cumplirse que $a+c\geq|b|$ y $b^2\leq 4a^2$, luego $4ac\leq b^2\leq 4a^2$ (ya que el polinomio tiene dos raíces reales y, por tanto, su discriminante $b^2-4ac$ es no negativo). Simplificando el factor positivo $4a$, se llega a que $c\leq a$.
• Supongamos ahora que $a+c\geq|b|$ y también que $a\geq c$. La primera de estas dos condiciones se traduce en que $p(1)$ y $p(-1)$ son no negativos. Ahora bien, elevándola al cuadrado y usando que $a\geq c$, tenemos que $b^2\leq (a+c)^2\leq(a+a)^2=4a^2$, por lo que el vértice de la parábola está en $[-1,1]$. Deducimos de todo esto que ambas raíces están en $[-1,1]$.

Nota. Podríamos haber empezado de la forma obvia, expresando la condición sobre las raíces como \[\frac{-b-\sqrt{b^2-4ac}}{2a}\geq -1,\qquad \frac{-b+\sqrt{b^2-4ac}}{2a}\leq 1.\] Estas desigualdades se traducen en que $\sqrt{b^2-4ac}\gt 2a+b$ y $\sqrt{b^2-4ac}\gt 2a-b$. Elevando al cuadrado, llegamos a que $a+c\geq |b|$ fácilmente. No obstante, puede ser difícil llegar a partir de aquí a la condición $a\geq c$... ¿Sabrías completar la demostración?

Solución. Llamemos $a_1,\ldots,a_8$ a las longitudes de los ocho lados del octógono, escritos de forma consecutiva. Vamos a demostrar que $a_1=a_5$ puesto que las otras igualdades $a_2=a_6$, $a_3=a_7$ y $a_4=a_8$ se demuestran de forma similar.

Para ello, vamos a tomar las rectas que contienen a los lados impares $a_1,a_3,a_5,a_7$. Como los ángulos interiores son iguales a $45º$, estas rectas son paralelas dos a dos y forman un rectángulo $R$. Además, si a $R$ le quitamos el octógono, quedarán cuatro triángulos rectángulos isósceles de hipotenusas $a_2,a_4,a_6,a_8$, por lo que sus catetos serán $\frac{a_2}{\sqrt{2}},\frac{a_4}{\sqrt{2}},\frac{a_6}{\sqrt{2}},\frac{a_8}{\sqrt{2}}$, respectivamente. Imponiendo ahora que los lados opuestos de $R$ deben tener igual longitud, nos quedan las relaciones $$\frac{a_4+a_6}{2}\sqrt{2}+a_5=\frac{a_8+a_2}{2}\sqrt{2}+a_1,\qquad \frac{a_2+a_4}{2}\sqrt{2}+a_3=\frac{a_6+a_8}{2}\sqrt{2}+a_7.$$ Si usamos finalmente que los lados tienen longitudes enteras, entonces los términos que multiplican a $\sqrt{2}$ deben ser iguales (ya que $\sqrt{2}$ es irracional, mientras que el resto de términos son racionales), lo que nos lleva a reformular las igualdades anteriores como $$\frac{a_4+a_6}{2}=\frac{a_8+a_2}{2},\qquad a_5=a_1,\qquad \frac{a_2+a_4}{2}\sqrt{2}=\frac{a_6+a_8}{2},\qquad a_3=a_7,$$ probando así la igualdad que queríamos.

Nota. ¿Es cierto el mismo resultado para un hexágono?

Solución. Como $2022=3\cdot674$ es múltiplo de $3$, podemos colocar $674$ personas dejando dos huecos entre ellas. De esta forma, cada silla libre está a la derecha o a la izquierda de una persona sentada y se cumple lo que dice el enunciado.

Sólo queda por ver que no se puede cumplir si se sientan $673$ personas o menos. Para verlo, dividimos los $2022$ asientos en $674$ grupos de $3$ asientos consecutivos. Si hay $673$ personas o menos, entonces no habrá ninguna persona sentada en alguno de esos grupos y la silla central de dicho grupo tendrá otra silla libre tanto a su derecha como a su izquierda.

Nota. El mismo razonamiento funciona con $3n$ sillas, siendo $n$ un número natural.