Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 435
Si $n\geq 3$ es un número impar, demostrar que la fracción $\frac{2}{n}$ se puede escribir como suma de dos fracciones con numerador $1$ y cuyos denominadores son números enteros distintos.
pistasolución 1info
Pista. Observa que $\frac{1}{n}=\frac{1}{n+1}+\frac{1}{n(n+1)}$.
Solución. Basta darse cuenta de la siguiente expresión:
$$\frac{2}{n}=\frac{1}{\frac{n+1}{2}}+\frac{1}{\frac{n(n+1)}{2}},$$
donde los números $\frac{n+1}{2}$ y $\frac{n(n+1)}{2}$ son ambos enteros por ser $n$ impar. Además, estos dos números son distintos por ser $n\geq 3$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 434
Sea $p(x)=x^n+nx^{n-1}+a_{n-2}x^{n-2}+\ldots+a_1x+a_0$ un polinomio de grado $n$ que tiene todas sus raíces reales $r_1,r_2,\ldots,r_n$. Encontrar dichas raíces si sabemos que $r_1^{16}+r_2^{16}+\ldots+r_n^{16}=n$.
pistasolución 1info
Pista. Usar la desigualdad de Cauchy-Schwarz para probar que $r_1^{16}+r_2^{16}+\ldots+r_n^{16}\geq n$ usando que $r_1+\ldots+r_n=-n$ y analizar en qué casos se da la igualdad.
Solución. El hecho de que el coeficiente del término de grado $n-1$ sea igual a $n$ nos dice que la suma de las raíces es $r_1+\ldots+r_n=-n$ (por las relaciones de Cardano-Vieta). La desigualdad de Cauchy-Schwarz aplicada a los vectores $(r_1,r_2,\ldots,r_n)$ y $(1,1,\ldots,1)$ nos dice que
$$n^2=(r_1+r_2+\ldots+r_n)^2\leq n(r_1^{2}+r_2^2+\ldots+r_n^2)$$
luego deducimos que $r_1^{2}+r_2^2+\ldots+r_n^2\geq n$. Volvemos a aplicar la desigualdad de Cauchy-Schwarz para obtener que
$$n^2\leq(r_1^2+r_2+\ldots+r_n^2)^2\leq n(r_1^{4}+r_2^2+\ldots+r_n^4),$$
de donde ahora deducimos que $r_1^{4}+r_2^4+\ldots+r_n^4\geq n$. Repitiendo el proceso dos veces más, tenemos que
\begin{align*}
n^2\leq(r_1^4+r_2^4+\ldots+r_n^4)^2\leq n(r_1^{8}+r_2^{8}+\ldots+r_n^8)\\
n^2\leq(r_1^8+r_2^8+\ldots+r_n^8)^2\leq n(r_1^{16}+r_2^{16}+\ldots+r_n^{16}),\\
\end{align*}
luego $r_1^{16}+r_2^{16}+\ldots+r_n^{16}\geq n$. El enunciado nos dice que se da la igualdad en esta desigualdad, luego también se debe dar en cada desigualdad de Cauchy-Schwarz, lo que nos dice que todos las raíces $r_1,\ldots,r_n$ son iguales. Como su suma es $-n$, llegamos finalmente a que $r_1=r_2=\ldots=r_n=-1$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 433
Para cada número natural $n\in\mathbb{N}$, definimos $a_n$ como el número real con parte entera $0$ y parte decimal las potencias $n$-ésimas de los naturales. Por ejemplo,
\begin{align*}
a_1&=0.1234567891011121314151617...\\
a_2&=0.149162536496481100121144...\\
a_3&=0.1827641252163435127291000...
\end{align*}
¿Es $a_n$ un número racional para algún valor de $n$?
pistasolución 1info
Pista. ¿Qué pasa con los números de la forma $10^{kn}$ contenidos en la expresión decimal de $a_n$?
Solución. Supongamos que $a_n$ es racional para cierto valor de $n$ y, por tanto, que su expresión decimal es periódica. Si llamamos $r$ a la longitud del período, como $10^{rn}$ tiene al menos $r$ ceros consecutivos y está contenido en la mantisa de $a_n$, deducimos necesariamente que el período es cero, es decir, que el número es un decimal exacto. Esto es una contradicción ya que hay infinitos decimales no nulos en $a_n$. Esta contradicción nos asegura que $a_n$ no es racional para ningún valor de $n$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 432
IMO, 1972-P1
Dado un subconjunto $A$ formado por $10$ elementos del conjunto $\{10,11,\ldots,99\}$, demostrar que existen dos subconjuntos disjuntos de $A$ cuyos elementos suman la misma cantidad.
pistasolución 1info
Pista. Usa el principio del palomar: ¡hay más subconjuntos que sumas posibles!
Solución. El conjunto $A$ tiene $10$ elementos, luego hay $2^{10}-1=1023$ subconjuntos distintos de $A$ no vacíos. Por otro lado, la suma mínima de elementos de uno de tales subconjuntos es $10+11+\ldots+19=185$ y la suma máxima $90+91+\ldots+99=945$, luego no hay más de $945-184=771$ sumas posibles distintas. Por el principio del palomar, habrá dos subconjuntos $B$ y $C$ de $A$ con la misma suma. Ahora basta con eliminar de $B$ y $C$ los elementos comunes, con lo que obtendremos los subconjuntos que queremos.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 431
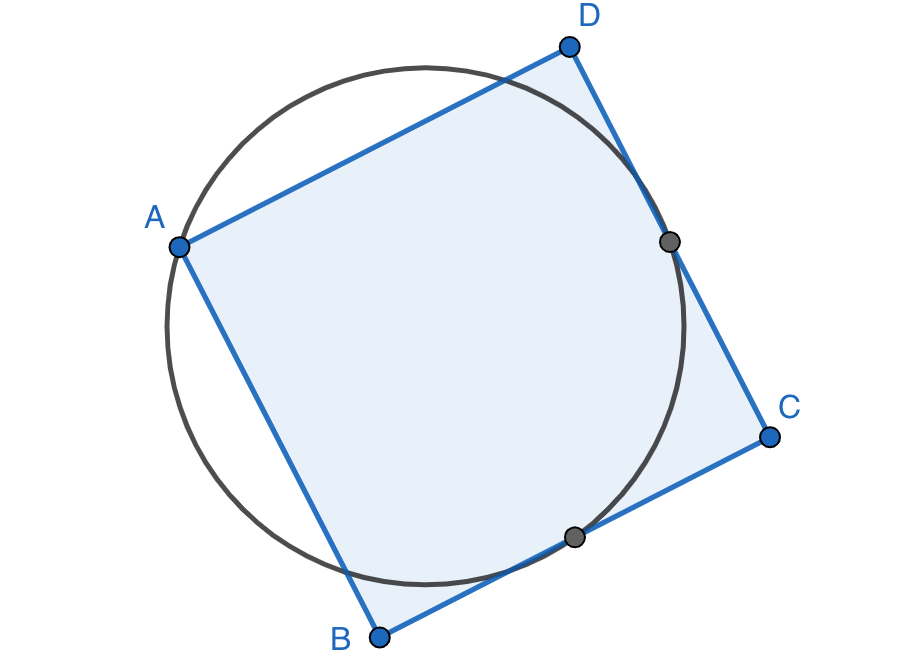
En un cuadrado $ABCD$ se traza una circunferencia que pasa por el vértice $A$ y por los puntos medios de los lados $BC$ y $CD$. Determinar si es mayor la longitud de la circunferencia o el perímetro del cuadrado.
pistasolución 1info
Pista. El teorema de Pitágoras puede ser útil.
Solución. Supongamos que el cuadrado tiene lado 1 sin perder generalidad. Sea $O$ el centro de la circunferencia y sean $M$ y $N$ los puntos medios de los lados $BC$ y $CD$. Llamando $P$ al punto medio de $MN$ y usando el teorema de Pitágoras se calcula fácilmente $AM=\frac{\sqrt{5}}{2}$ y $MP=\frac{1}{2}MN=\frac{\sqrt{2}}{4}$. Además, $AO=OM=R$, el radio de la circunferencia. Por lo tanto, el teorema de Pitágoras en los triángulos rectángulos $AMP$ y $OMP$ nos dice que
\[\frac{5}{4}=\frac{1}{8}+(R+OP)^2,\qquad R^2=OP^2+\frac{1}{8}.\]
Este sistema de dos ecuaciones con incógnitas $OP$ y $R$ se resuelve fácilmente, obteniendo como únicas soluciones positivas:
\[OP=\frac{\sqrt{2}}{3},\qquad R=\frac{5\sqrt{2}}{12}.\]
Por lo tanto, la longitud de la circunferencia es $2\pi R=\frac{5\sqrt{2}\pi}{6}$, mientras que el perímetro del cuadrado es $4$. Como $\pi^2<10<\frac{576}{50}$, tomando raíces cuadradas obtenemos que $\frac{5\sqrt{2}\pi}{6}<4$, es decir, la longitud de la circunferencia es menor que el perímetro del cuadrado.
Nota. El valor de $R$ también se deduce de la fórmula para el radio de la circunferencia circunscrita al triángulo $AMN$, es decir, \[R=\frac{MN\cdot AM\cdot AN}{\sqrt{p(p-MN)(p-AM)(p-AN)}},\] donde $p=\frac{1}{2}(AM+MN+AN)$ es el semiperímetro del triángulo.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre