Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 425
ASU, 1961-P7
En cada casilla de un tablero $m\times n$ se encuentra un número real. Se permite cambiar todos los números de una fila o de una columna de signo tantas veces como queramos. Demostrar que puede conseguirse que las sumas de los elementos cada fila y cada columna sean no negativas independientemente de la configuración inicial.
pistasolución 1info
Pista. Analiza la suma total de los elementos cuando cambias de signo una fila o una columna de suma negativa.
Solución. Sea $S$ la suma total de los elementos de la tabla. Cada vez que nos encontremos una fila o columna con suma negativa la cambiamos de signo. Cada una de estas operaciones incrementa el valor de $S$ y, como hay un número limitado de combinaciones de signos (es menor o igual que $2^{mn}$, el número de elecciones de signos $\pm$ en los $mn$ elementos de la tabla), este proceso no puede continuar indefinidamente, es decir, llegamos a un punto en el que todas las filas y columnas tienen suma positiva.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 424
OIM, 1989-P2
Sean $x,y,z$ tres números reales tales que $0\lt x\lt y\lt z\lt\frac{\pi}{2}$. Demostrar la siguiente desigualdad:
\[\frac{\pi}{2}+2\sin(x)\cos(y)+2\sin(y)\cos(z)\gt \sin(2x)+\sin(2y)+\sin(2z).\]
pistasolución 1info
Pista. Interpreta cada uno de los términos como el área de una figura plana.
Solución. Consideremos un cuarto de circunferencia donde hemos representado los valores de $x,y,z$ como ángulos tal y como muestra la figura. Entonces, el área del rectángulo rojo está dada por $\cos(z)\mathrm{sen}(z)=\frac{1}{2}\mathrm{sen}(2z)$, el área del rectángulo verde por $(\cos(y)-\cos(z))\mathrm{sen}(y)=\frac{1}{2}\mathrm{sen}(2y)-\mathrm{sen}(z)\cos(y)$ y la del rectángulo azul por $(\cos(x)-\cos(y))\mathrm{sen}(x)=\frac{1}{2}\mathrm{sen}(2x)-\mathrm{sen}(x)\cos(y)$. Entre todas suman menos que el área del cuarto de círculo $\frac{\pi}{4}$, de donde claramente se deduce la desigualdad del enunciado.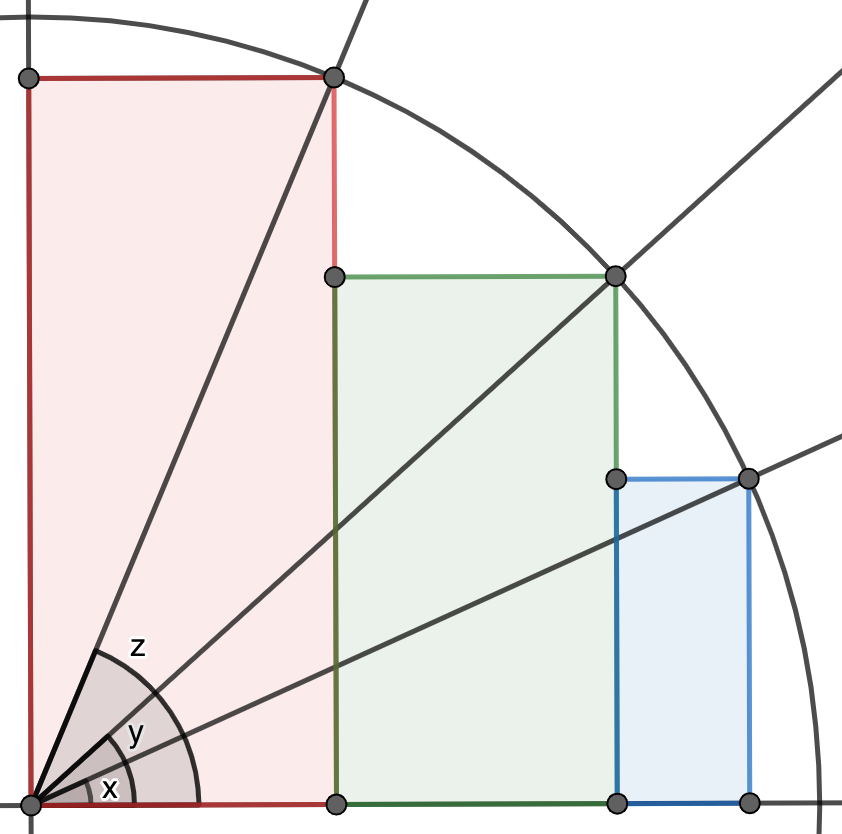

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 423
OIM, 1985-P4
Si $x$ e $y$ son números reales distintos y distintos de $1$ y además
\[\frac{yz-x^2}{1-x}=\frac{xz-y^2}{1-y},\]
demostrar que ambas fracciones son iguales a $x+y+z$.
pistasolución 1info
Pista. Resta $x+y+z$ de ambas fracciones y opera.
Solución. Restando $x+y+z$ de ambas fracciones, obtenemos la igualdad
\begin{eqnarray*}
\frac{yz-x^2}{1-x}-(x+y+z)&=&\frac{yz-x^2-(1-x)(x+y+z)}{1-x}=\frac{yz+xz+xy-x-y-z}{1-x},\\
\frac{xz-y^2}{1-y}-(x+y+z)&=&\frac{xz-y^2-(1-y)(x+y+z)}{1-y}=\frac{yz+xz+xy-x-y-z}{1-y}.\\
\end{eqnarray*}
Como estas fracciones han de ser iguales pero los denominadores son distintos (y distintos de cero), el numerador común debe ser cero, luego las fracciones iniciales eran iguales a $x+y+z$, como queríamos probar.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 422
OIM, 1985-P2
Sea $P$ un punto interior del triángulo equilátero $ABC$ tal que $PA=5$, $PB=7$ y $PC=8$. Hallar la longitud de un lado del triángulo $ABC$.
pistasolución 1solución 2info
Pista. Haz una rotación de $60º$ respecto del vértice $A$ e investiga relaciones entre áreas en la figura resultante.
Solución. Consideremos un giro de centro en $C$ y ángulo $60º$ que transforma $ABC$ en otro triángulo equilátero $A'B'C'$ con $B'=A$ y $C'=C$. Llamemos $P'$ al punto en el que se transforma $P$ por dicho giro. Entonces, está claro que $PP'C$ es es equilátero (ya que $PC=P'C$ y $\angle PCP'=60ª$) y $APP'$ tiene por lados $AP$, $AP'=BP$ y $PP'=CP$. Además, se cumple que
\[\text{área}(APP')+\text{área}(CPP')=\text{área}(AP'C)+\text{área}(APC)=\text{área}(BPC)+\text{área}(APC).\]
Si llamamos $\Delta_a$ a un triángulo equilátero de lado $a$ y $T$ al triángulo de lados $5$, $7$ y $8$, tenemos que
\[\text{área}(\Delta_8)+\text{área}(T)=\text{área}(BPC)+\text{área}(APC).\]
Análogamente, haciendo giros de $60º$ respecto de los vértices $A$ y $B$, tenemos que
\begin{eqnarray*}
\text{área}(\Delta_7)+\text{área}(T)&=\text{área}(APB)+\text{área}(BPC),\\
\text{área}(\Delta_5)+\text{área}(T)&=\text{área}(APB)+\text{área}(APC).
\end{eqnarray*}
Sumando las tres igualdades y teniendo en cuenta que las áreas de los tres triángulos $APB$, $BPC$ y $APC$ suman el área de $\Delta_\ell$, siendo $\ell$ el lado del triángulo $ABC$, llegamos a la identidad
\[\text{área}(\Delta_5)+\text{área}(\Delta_7)+\text{área}(\Delta_8)+3\cdot\text{área}(T)=2\cdot\text{área}(\Delta_\ell).\]
Usando que $\text{área}(\Delta_a)=\frac{\sqrt{3}}{4}a^2$ y que la fórmula de Herón nos dice que $\text{área}(T)=\sqrt{p(p-5)(p-7)(p-8)}=10\sqrt{3}$, siendo $p=10$ el semiperímetro de $T$, podemos transformar la identidad anterior en la ecuación
\[(5^2+7^2+8^2)\frac{\sqrt{3}}{4}+30\sqrt{3}=\frac{\sqrt{3}}{2}\ell^2,\]
de donde deducimos que $\ell=\sqrt{129}$.
Solución. Vamos a introducir coordenadas para resolver el problema. Para simplificar los cálculos, tomemos el origen de coordenadas en el vértice $C$ y el eje de abscisas sobre el lado $BC$, de forma que los tres vértices tengan coordenadas
\[A=\left(\frac{\ell}{2},\frac{\sqrt{3}}{2}\ell\right),\qquad B=(\ell,0),\qquad C=(0,0),\]
siendo $\ell$ el lado del triángulo equilátero $ABC$. Si tomamos $P=(x,y)$, las condiciones dadas en el enunciado pueden reescribirse como
\begin{eqnarray*}
d(A,P)=5&\Leftrightarrow&\left(x-\frac{\ell}{2}\right)^2+\left(y-\frac{\sqrt{3}}{2}\ell\right)^2=25,\\
d(B,P)=7&\Leftrightarrow&(x-\ell^2)+y^2=49,\\
d(C,P)=8&\Leftrightarrow&x^2+y^2=64.\\
\end{eqnarray*}
Usando la tercera ecuación para eliminar los cuadrados de $x$ en $y$ en las dos primeras, podemos despejar $x$ e $y$ en función de $\ell$ como
\[x=\frac{\ell^2+15}{2\ell},\qquad y=\frac{\ell^2+63}{2\sqrt{3}\ell}.\]
Imponiendo finalmente que $x^2+y^2=64$, obtenemos la ecuación
\[\left(\frac{\ell^2+15}{2\ell}\right)^2+\left(\frac{\ell^2+63}{2\sqrt{3}\ell}\right)^2=64\ \Leftrightarrow\ \ell^4-138\ell^2+1161=0.\]
Esta ecuación bicuadrada tiene como soluciones positivas $\ell=\sqrt{129}$ y $\ell=3$, aunque ésta última debe descartarse ya que el punto $P$ ha de ser interior al triángulo.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 421
Encontrar todos los polinomios $P(x)$ y $Q(x)$ con coeficientes reales que cumplen que
\[P(Q(x))=(x-1)(x-2)(x-3)(x-4).\]
pistasolución 1info
Pista. ¿Qué grados pueden tener los polinomios $P$ y $Q$?
Solución. Observamos que el grado de $P(Q(x))$ es el producto de los grados de $P(x)$ y $Q(x)$. Llamando $R(x)=(x-1)(x-2)(x-3)(x-4)$, como el grado de $R(x)$ es $4$, tenemos varias posibilidades:
- Si $P(x)$ tiene grado $1$, entonces $P(x)=ax+b$ para ciertos $a,b\in\mathbb{R}$ con $a\neq 0$ y, por consiguiente, $Q(x)=\frac{1}{a}(R(x)-b)$.
- Si $P(x)$ tiene grado $4$, entonces $Q(x)$ tiene grado $1$, es decir, $Q(x)=ax+b$ para ciertos $a,b\in\mathbb{R}$ con $a\neq 0$. Por tanto, $P(x)=R(\frac{1}{a}x-b)$.
- Si $P(x)$ y $Q(x)$ tienen ambos grado 2 y escribimos $P(x)=a(x-\alpha_1)(x-\alpha_2)$ para ciertos valores de $a\in\mathbb{R}$ no nulo y $\alpha_1,\alpha_2\in\mathbb{C}$, entonces tenemos que \[P(Q(x))=a(Q(x)-\alpha_1)(Q(x)-\alpha_2)=(x-1)(x-2)(x-3)(x-4).\] Sustituyendo $x=1,2,3,4$ obtenemos que los números $Q(1),Q(2),Q(3),Q(4)$ son iguales a $\alpha_1$ ó $\alpha_2$. Como $Q$ tiene grado 2, no puede tomar más de dos veces el mismo valor, luego dos de los números $Q(1),Q(2),Q(3),Q(4)$ serán iguales a $\alpha_1$ y dos a $\alpha_2$. Para que esto ocurra, la parábola dada por $Q(x)$ ha de tener su vértice en $x=\frac{5}{2}$, es decir, $Q(x)=b(x-\frac{5}{2})^2+c$ para ciertos valores de $b,c\in\mathbb{R}$ con $b\neq 0$. Y además $\alpha_1=Q(1)=Q(4)=\frac{9}{4}b+c$ y $\alpha_2=Q(2)=Q(3)=\frac{1}{4}b+c$. Finalmente, para que el coeficiente líder de $P(Q(x))$ sea igual a $1$, tenemos que tomar $a=\frac{1}{b^2}$, con lo que queda \[P(x)=\frac{1}{b^2}\left(x-\frac{9}{4}b-c\right)\left(x-\frac{1}{4}b-c\right),\qquad Q(x)=b\left(x-\frac{5}{2}\right)^2+c,\] para cualesquiera $b,c\in\mathbb{R}$ con $b\neq 0$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre