Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
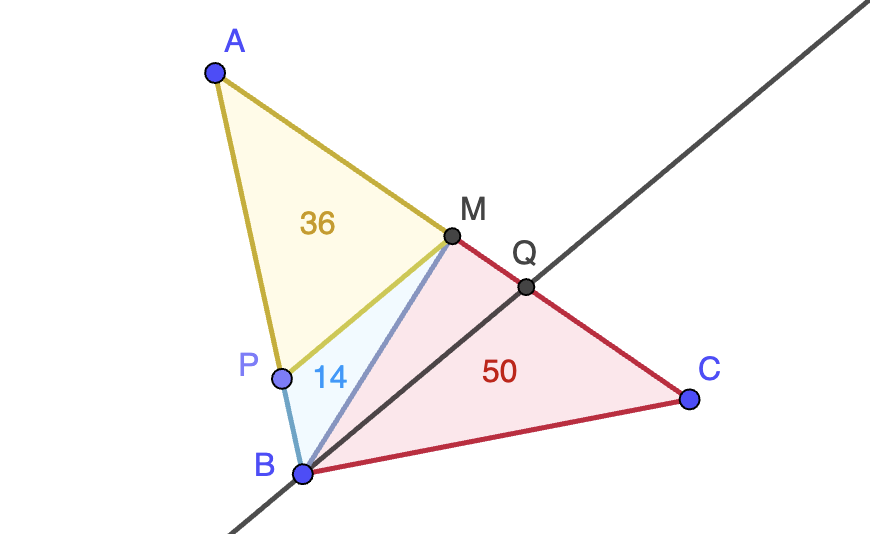
Informar de error en enunciado Informar de procedencia del problema
Nota. No es difícil terminar el razonamiento y ver que las soluciones al problema son \[(a,b)=\left(21\sqrt{3},5\sqrt{3}\right)\qquad\text{y}\qquad (a,b)=\left(-21\sqrt{3},-5\sqrt{3}\right).\]
Informar de error en enunciado Informar de procedencia del problema
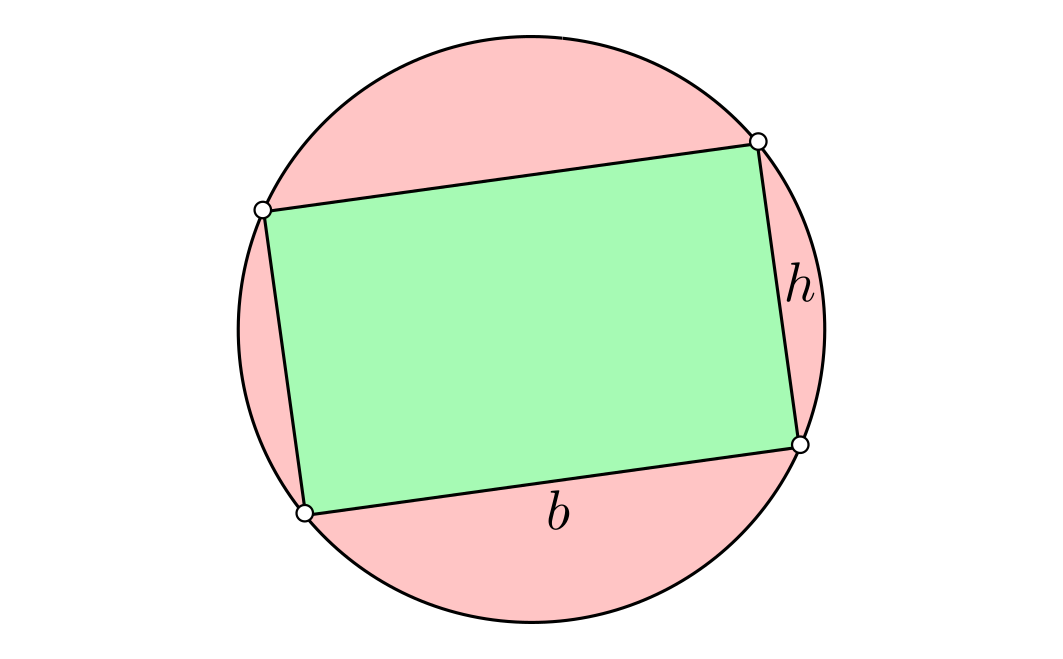
Nota. Otra opción para finalizar el ejercicio es darse cuenta de que el siguiente cociente es mayor que $1$: \[\frac{A}{A'}=\frac{\frac{b}{h}}{\frac{\pi}{4}((\frac{b}{h})^2+1)-\frac{b}{h}}=\frac{\frac{1+\sqrt{5}}{2}}{\frac{\pi}{4}((\frac{1+\sqrt{5}}{2})^2+1)-\frac{1+\sqrt{5}}{2}}\approx 1.32,\] donde hemos dividido numerador y denominador por $h^2$ para poder aplicar ($\star$). Una alternativa a esto último es suponer a lo largo de todo el razonamiento que $h=1$ haciendo previamente una homotecia.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Nota. No se puede expresar el resultado final en términos de funciones trigonométricas.
En el pentágono regular de lado $1$ de la figura, los triángulos $ACD$ y $DEP$ son semejantes pues sus lados son paralelos. Si llamamos $d$ a la longitud de la diagonal del pentágono, la semejanza $\frac{AD}{CD}=\frac{DE}{PE}$ se escribe como $\frac{d}{1}=\frac{1}{d-1}$, de donde $d$ cumple la ecuación $d^2-d-1=0$, de la que nos quedamos con la única solución positiva $d=\frac{1+\sqrt{5}}{2}$, la razón áurea. Ahora bien, el triángulo $ABQ$ de la figura es rectángulo y cumple $\angle BAQ=54$, luego \begin{align*}
\mathrm{sen}(54)&=BD=\frac{d}{2}=\frac{1+\sqrt{5}}{4},\\
\cos(54)&=AQ=\sqrt{1-BQ^2}=\sqrt{1-\left(\tfrac{1+\sqrt{5}}{4}\right)^2}=\frac{\sqrt{5-\sqrt{5}}}{2\sqrt{2}}.
\end{align*}
De esta forma, tenemos que el área del triángulo es
\[8\,\mathrm{sen}(54)\cos(54)=8\frac{1+\sqrt{5}}{4}\cdot\frac{\sqrt{5-\sqrt{5}}}{2\sqrt{2}}=\sqrt{10+2\sqrt{5}}.\]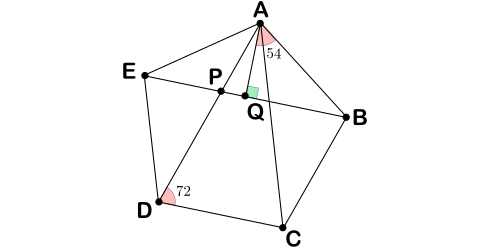
Informar de error en enunciado Informar de procedencia del problema