Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Consideremos un triángulo $ABC$, su circuncentro $O$ y su ortocentro $H$. Si llamamos $M$ al punto medio del lado $BC$, tendremos que demostrar que $AH=2BC$. Para ello, trazamos el diámetro de la circunferencia circunscrita que pasa por $B$ y su punto diametralmente opuesto, que llamaremos $P$, como se indica en la figura. Por ser $BP$ un diámetro, se tiene que $PC$ es perpendicular a $BC$ y, por tanto, paralela a la mediatriz $OM$. Entonces, los triángulos $BOM$ y $BPC$ son semejantes y se cumple que $PC=2OM$, luego tendremos que demostrar que $PC=AH$. Esto último se sigue de que $APCH$ es un paralelogramo ya que $PC$ es paralela a la altura $AH$ y $AP$ es paralela a la altrua $CH$ (ya que el ángulo $\angle BAP$ es recto por comprender al diámetro $BP$).

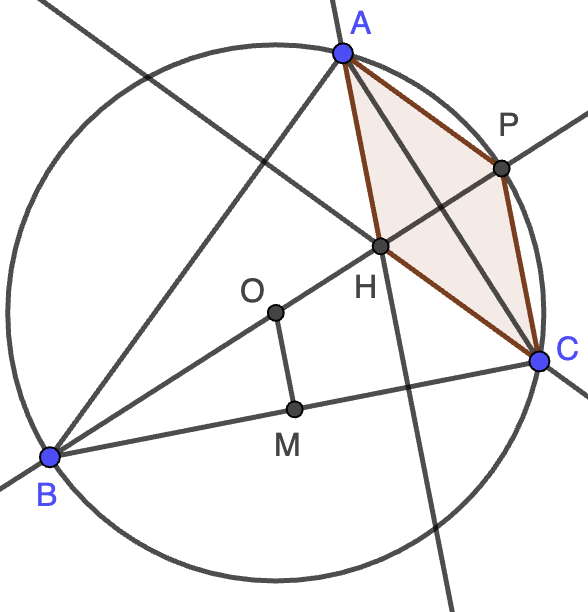
Nota. Este es un resultado relativamente conocido en el ámbito de la geometría de olimpiadas. ¿Sabrías probar que $AH=2R\cos A$ y $OM=R\cos A$, siendo $R$ el radio de la circunferencia circunscrita? ¿Sabrías probar a partir de este resultado que las rectas $OA$ y $MH$ se cortan en un punto de la circunferencia circunscrita?

Solución. Consideremos los seis triángulos en que la figura queda dividida por las cevianas $AF$, $BD$ y $CE$ y llamemos a sus áreas $S_1,\ldots,S_6$ tal y como se indica en la figura. Vamos a obtener relaciones entre estas áreas usando que las áreas de dos triángulos que tienen la misma altura son proporcionales a las bases.

• El triángulo $APC$ tiene el triple del área de $AEP$ ya que tienen el altura común en $A$ y las bases son $9$ y $3$, respectivamente. Esto nos dice que $S_1+S_2=3S_6$.
• Los triángulos $BPC$ y $EPB$ están en la misma situación, lo que nos dice que $S_3+S_4=3S_5$.
• Los triángulos $APB$ y $APD$ tienen el mismo área ya que tienen iguales la base y la altura desde el vértice común $A$. Deducimos así que $S_5+S_6=S_1$.
• Los triángulos $EPB$ y $CPD$ tienen un ángulo igual (opuesto por el vértice $P$), luego rotando uo de ellos $180^\circ$ respecto de $P$, como $BP=PD$, deducimos que $S_2=3S_3$ (también puede usarse que el área es $\frac{1}{2}$ del producto de dos lados por el seno del ángulo que forman).

Con todo esto, tenemos tres ecuaciones lineales que involucran a las incógnitas $S_1$, $S_2$, $S_5$, $S_6$ y $S_3+S_4$. El sistema no es compatible determinado pero nos permite despejar en términos de $S_1$ el resto de áreas (¡compruébalo!): \[S_2=S_1,\qquad S_6=\frac{2}{3}S_2,\qquad S_5=\frac{1}{3}S_1,\qquad S_3+S_4=S_1.\] Ahora bien, si llamamos $x=AP$ y $20-x=PF$, podemos hacer un truco similar a los anteriores ya que las áreas de $APC$ y $PFC$ son proporcionales a $x$ y $20-x$ y también lo son las de $APB$ y $PBF$. Esto nos da las relaciones siguientes: \[\frac{S_1+S_2}{x}=\frac{S_3}{20-x},\qquad \frac{S_5+S_6}{x}=\frac{S_4}{20-x}.\] Sumando ambas expresiones y poniendo todo en función de $S_1$, nos queda \[\frac{S_1+S_2+S_5+S_6}{x}=\frac{S_4+S_5}{20-x}\ \Longleftrightarrow\ \frac{3S_1}{x}=\frac{S_1}{20-x}.\] Eliminando $S_1$ de ambos miembros, la ecuación se resuelve fácilmente y nos da $x=15$. Por lo tanto, también podemos despejar $S_3$ y $S_4$ en términos de $S_1$: \[S_3=\frac{20-x}{x}(S_1+S_2)=\frac{2}{3}S_1,\qquad S_4=\frac{20-x}{x}(S_5+S_6)=\frac{1}{3}S_1.\]

Ya solamente nos queda calcular $S_1$ y esta es la parte difícil. Como $S_1=S_2$, se sigue que $D$ es el punto medio de $AC$, luego $PD$ es la mediana de $APC$. La mediana puede calcularse en función de los lados como \[36=AD^2=\frac{AP^2+PC^2}{2}-\frac{AC^2}{4}=\frac{15^2+9^2}{2}-\frac{AC^2}{4}\ \Leftrightarrow\ AC^2=468,\] de donde $CD=\frac{1}{2}AC=\sqrt{117}$. Como $PC^2+PD^2=9^2+6^2=117$, el triángulo $DPC$ es rectángulo. y podemos calcular $S_1=S_2=\frac{1}{2}\cdot 6\cdot 9=27$. Por tanto, el área de $ABC$ es \[S_1+S_2+S_3+S_4+S_5+S_6=S_1+S_1+\frac{2}{3}S_1+\frac{1}{3}S_1+\frac{1}{3}S_1+\frac{2}{3}S_1=4S_1=108.\]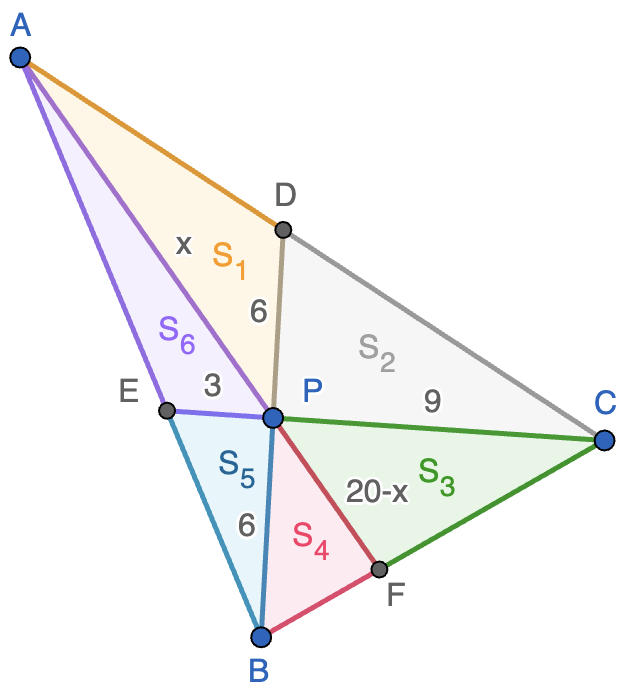

Nota. Si no nos damos cuenta en el paso final de que el triángulo es rectángulo, siempre podríamos haber usado la fórmula de Herón en $APD$. Es relativamente difícil caer en la cuenta de que $DPC$ es rectángulo (al escribir esta solución, se vio lo del triángulo rectángulo por haberlo dibujado previamente con Geogebra).

Solución. Vamos a ver que es imposible incluso si son de distinto tamaño por reducción al absurdo. Si el cubo se pudiera descomponer en un cierto número (finito) de tetraedros, como tales tetraedros definirán un número finito de vértices, habrá algún punto $P$ de una arista del cubo donde no llegará ningún vértice de ninguno de los tetraedros, lo que nos dice que a $P$ sólo llegan aristas de los tetraedros (no pueden llegar puntos interiores ni interiores a las caras ya que en tal caso los tetraedros se saldrían del cubo). De hecho, las aristas tienen que estar contenidas en las aristas del cubo, lo que nos dice que el ángulo diedro de $90^\circ$ que forman las dos caras del cubo que se encuentran en $P$ debe ser suma de un cierto número de veces el ángulo diedro $\alpha$ que forman las caras de un tetraedro regular $T$.

Para calcular $\alpha$, podemos suponer que $T$ tiene lado $1$. Seccionando $T$ por un plano que contiene a una de sus aristas y al punto medio de la arista opuesta. El triángulo en la intersección es isósceles y tiene un lado de longitud $1$, la arista de $T$, y los otros dos de longitud $\frac{\sqrt{3}}{2}$, la altura de una de las caras de $T$. El ángulo que buscamos es el que forman estos dos lados iguales, que puede calcularse como \[\alpha=2\,\mathrm{arcsen}\left(\frac{1/2}{\sqrt{3}/2}\right)=2\,\mathrm{arcsen}\left(\frac{1}{\sqrt{3}}\right)\gt 2\,\mathrm{arcsen}\left(\frac{1}{2}\right)=60^\circ.\] Además, está claro que $\alpha\lt 90^\circ$, por lo que no pueden completarse $90^\circ$ sumando un cierto número entero de ángulos iguales a $\alpha$.

Solución. Por comodidad, llamamos $\alpha=\angle CAL=\angle ABH=\angle BCM$. Como $AL$ es bisectriz, tenemos que $\angle BAH=2\alpha$, luego la suma de los ángulos del triángulo $ABH$ es $90^\circ+3\alpha=180^\circ$, de donde obtenemos que $\alpha=30^\circ$.

Sea $X$ el punto de la recta $AC$ tal que $H$ es el punto medio de $AX$, luego el triángulo $ABX$ es equilátero. Por un lado, como $MH$ y $BX$ son paralelas, ya que $M$ y $H$ son los puntos medios de los lados $AB$ y $AX$, el triángulo $AMH$ es equilátero y se tiene que $\angle MHB=90^\circ-\angle AHM=30^\circ$. Por otro lado, $\angle BMH=30^\circ$ ya que $XM$ es bisectriz en el triángulo equilátero $ABX$. La propiedad del arco capaz nos dice ahora que el cuadrilátero $BMHX$ tiene circunferencia circunscrita (los puntos desde los que $BM$ se ve con un ángulo de $30^\circ$) y que el punto $C$ tiene que estar sobre dicha circunferencia. Como la intersección de la circunferencia con la recta $AC$ son los puntos $H$ y $X$, la propiedad deseada se cumple si, y sólo si, $C=H$ o bien $C=X$. Tenemos así dos casos:

• Si $C=H$, entonces $ABC$ tiene ángulos $A=60^\circ$, $B=30^\circ$ y $C=90^\circ$.
• Si $C=X$, entonces $ABC$ tiene ángulos $A=B=C=60^\circ$.

Solución. Consideramos el circuncentro $O$ y el triángulo $OBC$, que está sombreado en la figura. Por un lado, tenemos que $\angle BCD=\frac{C}{2}$, por ser $BD$ la bisectriz, luego $\angle OCB=\frac{C}{4}$ ya que $OC$ es bisectriz del triángulo $BCD$. Por otro lado, tenemos que $\angle OBC=\frac{B}{2}$ ya que $OB$ es bisectriz de $BCD$. Finalmente, tenemos que $\angle BOC=2A$ ya que se trata del ángulo central del ángulo $A$ en el triángulo $ABC$.

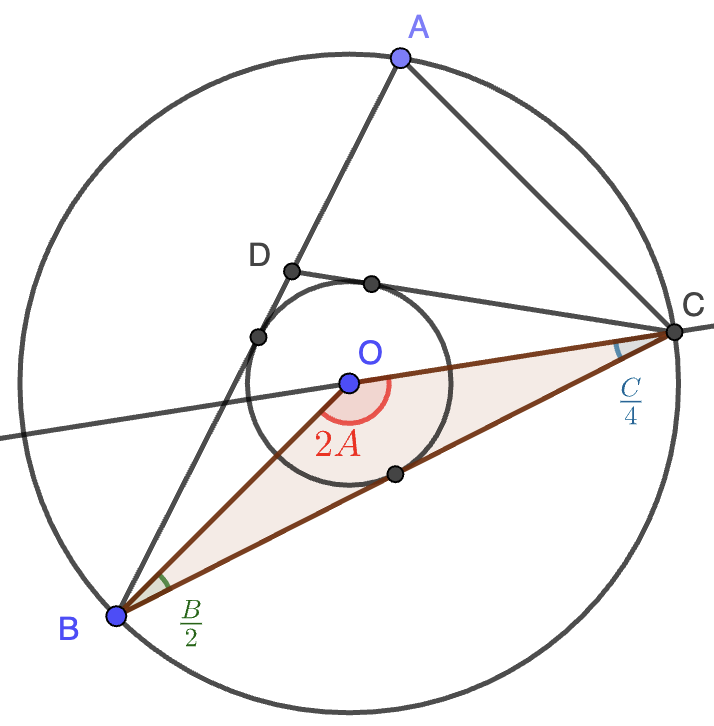
Tenemos así que $OBC$ tiene ángulos $2A$, $\frac{B}{2}$ y $\frac{C}{4}$. Este triángulo es isósceles dado que $OB=OC$ (son el radio de la circunferencia circunscrita), luego $\frac{C}{4}=\frac{B}{2}$. Nos quedan por tanto, tres ecuaciones sobre las incógnitas $A,B,C$, que forman el sistema lineal: \[\left\{\begin{array}{c} A+B+C=180\\ 2A+\frac{B}{2}+\frac{C}{4}=180\\ \frac{C}{4}=\frac{B}{2} \end{array}\right.\] Se resuelve fácilmente, dando solución única $A=C=72^\circ$ y $B=36^\circ$.