Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Vamos a ver que es imposible incluso si son de distinto tamaño por reducción al absurdo. Si el cubo se pudiera descomponer en un cierto número (finito) de tetraedros, como tales tetraedros definirán un número finito de vértices, habrá algún punto $P$ de una arista del cubo donde no llegará ningún vértice de ninguno de los tetraedros, lo que nos dice que a $P$ sólo llegan aristas de los tetraedros (no pueden llegar puntos interiores ni interiores a las caras ya que en tal caso los tetraedros se saldrían del cubo). De hecho, las aristas tienen que estar contenidas en las aristas del cubo, lo que nos dice que el ángulo diedro de $90^\circ$ que forman las dos caras del cubo que se encuentran en $P$ debe ser suma de un cierto número de veces el ángulo diedro $\alpha$ que forman las caras de un tetraedro regular $T$.

Para calcular $\alpha$, podemos suponer que $T$ tiene lado $1$. Seccionando $T$ por un plano que contiene a una de sus aristas y al punto medio de la arista opuesta. El triángulo en la intersección es isósceles y tiene un lado de longitud $1$, la arista de $T$, y los otros dos de longitud $\frac{\sqrt{3}}{2}$, la altura de una de las caras de $T$. El ángulo que buscamos es el que forman estos dos lados iguales, que puede calcularse como \[\alpha=2\,\mathrm{arcsen}\left(\frac{1/2}{\sqrt{3}/2}\right)=2\,\mathrm{arcsen}\left(\frac{1}{\sqrt{3}}\right)\gt 2\,\mathrm{arcsen}\left(\frac{1}{2}\right)=60^\circ.\] Además, está claro que $\alpha\lt 90^\circ$, por lo que no pueden completarse $90^\circ$ sumando un cierto número entero de ángulos iguales a $\alpha$.

Solución. Por comodidad, llamamos $\alpha=\angle CAL=\angle ABH=\angle BCM$. Como $AL$ es bisectriz, tenemos que $\angle BAH=2\alpha$, luego la suma de los ángulos del triángulo $ABH$ es $90^\circ+3\alpha=180^\circ$, de donde obtenemos que $\alpha=30^\circ$.

Sea $X$ el punto de la recta $AC$ tal que $H$ es el punto medio de $AX$, luego el triángulo $ABX$ es equilátero. Por un lado, como $MH$ y $BX$ son paralelas, ya que $M$ y $H$ son los puntos medios de los lados $AB$ y $AX$, el triángulo $AMH$ es equilátero y se tiene que $\angle MHB=90^\circ-\angle AHM=30^\circ$. Por otro lado, $\angle BMH=30^\circ$ ya que $XM$ es bisectriz en el triángulo equilátero $ABX$. La propiedad del arco capaz nos dice ahora que el cuadrilátero $BMHX$ tiene circunferencia circunscrita (los puntos desde los que $BM$ se ve con un ángulo de $30^\circ$) y que el punto $C$ tiene que estar sobre dicha circunferencia. Como la intersección de la circunferencia con la recta $AC$ son los puntos $H$ y $X$, la propiedad deseada se cumple si, y sólo si, $C=H$ o bien $C=X$. Tenemos así dos casos:

• Si $C=H$, entonces $ABC$ tiene ángulos $A=60^\circ$, $B=30^\circ$ y $C=90^\circ$.
• Si $C=X$, entonces $ABC$ tiene ángulos $A=B=C=60^\circ$.

Solución. Consideramos el circuncentro $O$ y el triángulo $OBC$, que está sombreado en la figura. Por un lado, tenemos que $\angle BCD=\frac{C}{2}$, por ser $BD$ la bisectriz, luego $\angle OCB=\frac{C}{4}$ ya que $OC$ es bisectriz del triángulo $BCD$. Por otro lado, tenemos que $\angle OBC=\frac{B}{2}$ ya que $OB$ es bisectriz de $BCD$. Finalmente, tenemos que $\angle BOC=2A$ ya que se trata del ángulo central del ángulo $A$ en el triángulo $ABC$.

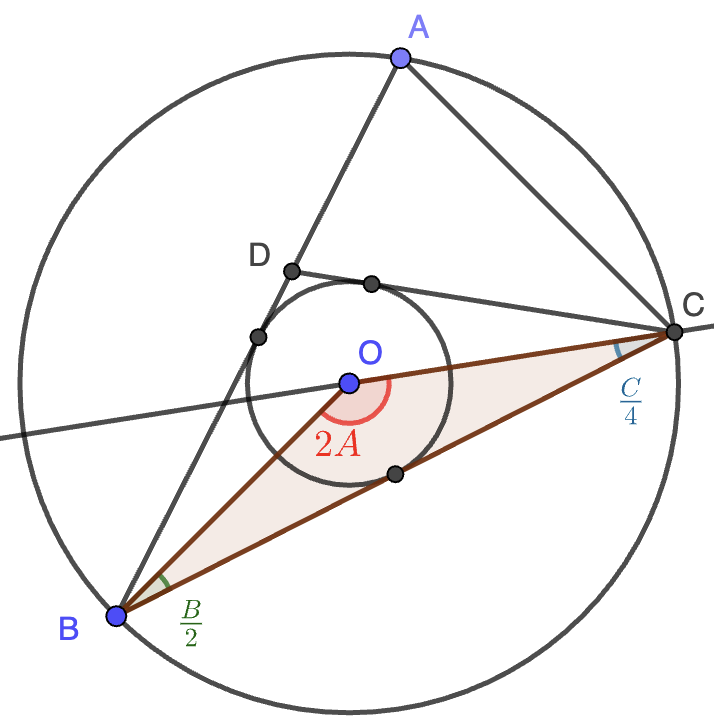
Tenemos así que $OBC$ tiene ángulos $2A$, $\frac{B}{2}$ y $\frac{C}{4}$. Este triángulo es isósceles dado que $OB=OC$ (son el radio de la circunferencia circunscrita), luego $\frac{C}{4}=\frac{B}{2}$. Nos quedan por tanto, tres ecuaciones sobre las incógnitas $A,B,C$, que forman el sistema lineal: \[\left\{\begin{array}{c} A+B+C=180\\ 2A+\frac{B}{2}+\frac{C}{4}=180\\ \frac{C}{4}=\frac{B}{2} \end{array}\right.\] Se resuelve fácilmente, dando solución única $A=C=72^\circ$ y $B=36^\circ$.

Solución. El área del triángulo es $2$ y el área del sector circular de arco $\ell$ (en azul en la figura) es $\frac{1}{8}\pi r^2$, siendo $r$ su radio. Esto viene de que es un octavo del círculo de radio $r$ ya que el ángulo $A$ del triángulo rectángulo isósceles $ABC$ es $45^\circ$. Igualando a la mitad del área del triángulo, obtenemos \[\tfrac{1}{8}\pi r^2=1\ \Longleftrightarrow\ r=2\sqrt{\tfrac{2}{\pi}}.\] Observamos que $r\lt 2$, lo que nos dice que el sector realmente está bien definido. Ahora bien, el radio $s$ del sector de arco $m$ (en naranja en la figura) sumado con $r$ nos da la hipotenusa $AB=2\sqrt{2}$, luego podemos despejar \[s=AB-r=2\sqrt{2}-2\sqrt{\tfrac{2}{\pi}}=2\sqrt{2}(1-\tfrac{1}{\sqrt{\pi}}).\] Tenemos entonces que el área que nos piden (en verde en la figura) es \[2-\tfrac{\pi}{8}r^2-\tfrac{\pi}{8}s^2=2-1-\tfrac{8\pi}{8}(1-\tfrac{1}{\sqrt{\pi}})^2=2\sqrt{\pi}-\pi.\]

Solución. Si recortamos el cuadrado y también el triángulo $CPQ$, podemos doblar por las líneas $AP$ y $AQ$ para formar una pirámide con vértice en $A$. Observemos que, de esta forma $B$ se identifica con $D$ ya que ambos puntos están a la misma distancia de $A$. No obstante, para comprobar que efectivamente la pirámide se cierra, observamos que el triángulo de vértices $B=D$, $P$ y $Q$ en el espacio es rectángulo ya que es congruente con el triángulo $CPQ$ que hemos quitado. Ahora la solución al problema es evidente ya que $BX$, $XY$ y $DY$ forman un triángulo en el espacio.