Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 767
OIM, 2003-P2
Sean $C$ y $D$ dos puntos de la semicircunferencia de diámetro $AB$ tales que $B$ y $C$ están en semiplanos distintos respecto de la recta $AD$. Denotemos por $M$, $N$ y $P$ los puntos medios de $AC$, $DB$ y $CD$, respectivamente. Sean $O_A$ y $O_B$ los circuncentros de los triángulos $ACP$ y $BDP$. Demostrar que las rectas $O_AO_B$ y $MN$ son paralelas.
pistasolución 1info
Pista. Demuestra que $OO_AO_B$ y $OMN$ son semejantes, siendo $O$ el centro de la semicircunferencia. Te puede ser útil utilizar el teorema de Thales.
Solución. Las mediatriz de $AC$ pasa por $O_A$ y por el centro $O$ de la semicircunferencia y, de la misma forma, la mediatriz de $BD$ pasa por $O_B$ y por $O$. Por tanto, que $O_AO_B$ sea paralela a $MN$ equivale a que los triángulos $OO_AO_B$ y $OMN$ sean semejantes. Si trazamos perpendiculares a la recta $CD$ que pasan por $A$, $M$, $O_A$, $O_B$, $N$ y $B$ (en línea discontinua en la figura) y marcamos los puntos de intersección con $CD$ como $E$, $F$, $G$, $H$, $I$ y $J$, respectivamente, el teorema de Thales nos dice que
\[\frac{OO_A}{GP}=\frac{OM}{PF},\qquad \frac{OO_B}{HP}=\frac{ON}{PI}.\]
Utilizando que $G$ y $H$ son los puntos medios de $CP$ y $DP$ (ya que las perpendiculares por $O_A$ y $O_B$ son mediatrices de $CP$ y $DP$, respectivamente), las semejanzas anteriores se reescriben como
\[\frac{OO_A}{OM}=\frac{CP}{2PF},\qquad \frac{OO_B}{ON}=\frac{DP}{2PI}.\]
Como $CP=DP$ por ser $P$ el punto medio de $CD$, el problema estará resuelto si demostramso que $PF=PI$. Usando de nuevo que $CP=DP$, podemos reducir el problema aún más a probar que $PE=PJ$, pero esto último es sencillo ya que es consecuencia del teorema de Thales aplicado a las paralelas $BJ$, $OP$ y $AE$ que cortan a las rectas $AB$ y $AJ$, teniendo en cuenta que $O$ es el punto medio de $AB$.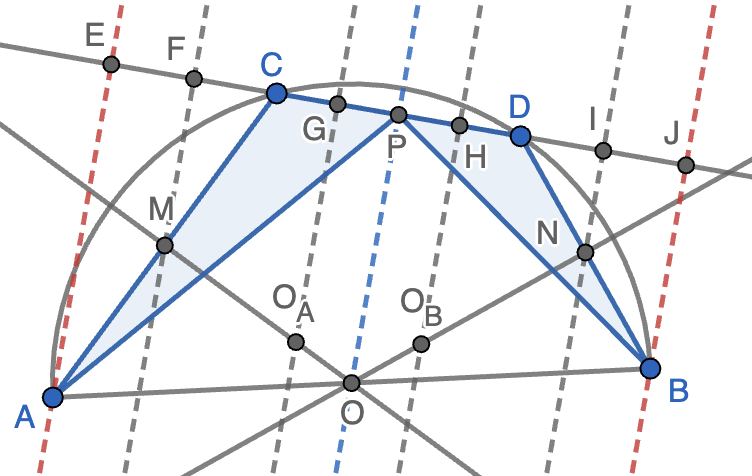

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 764
OIM, 2002-P4
En un triángulo escaleno $ABC$ se traza la bisectriz interior $BD$, con $D$
sobre $AC$. Sean $E$ y $F$, respectivamente, los pies de las perpendiculares trazadas desde $A$ y $C$ hacia la recta $BD$ y $M$ el punto sobre el lado $BC$ tal que $DM$ es perpendicular a $BC$. Demostrar que $\angle EMD=\angle DMF$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 763
OIM, 2002-P3
Un punto $P$ interior al triángulo equilátero $ABC$ es tal que $\angle APC=120^\circ$. Sean $M$ la intersección de $CP$ con $AB$ y $N$ la intersección de $CP$ con $BC$. Hallar el lugar geométrico del circuncentro del triángulo $MBN$ al variar $P$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 759
OIM, 2001-P2
La circunferencia inscrita en el triángulo $ABC$ tiene centro $O$ y es tangente a los lados $BC$, $AC$ y $AB$ en los puntos $X$, $Y$ y $Z$, respectivamente. Las rectas $BO$ y $CO$ cortan a la recta $YZ$ en los puntos $P$ y $Q$, respectivamente. Si los segmentos $XP$ y $XQ$ tienen la misma longitud, demostrar que el triángulo $ABC$ es isósceles.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 757
OIM, 2000-P6
Un hexágono convexo se denomina bonito si tiene cuatro diagonales de longitud $1$ cuyos extremos incluyen todos los vértices del hexágono.
- Dado cualquier número $k$ mayor que $0$ y menor que $1$, encontrar un hexágono bonito de área $k$.
- Demostrar que el área de cualquier hexágono bonito es menor que $\frac{3}{2}$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre