Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
- Calcular las medidas de los ángulos del triángulo $BCD$.
- Expresar la medida del lado $BC$ en función de la medida del lado $AC$, sin que en la expresión aparezcan razones trigonométricas.
El triángulo $ABD$ también es isósceles por tener dos ángulos iguales a $36^\circ$, luego $BC=BD=AD$. Además, $BCD$ y $ABC$ son semejantes por tener los ángulos iguales, luego
\[\frac{AC}{BC}=\frac{BC}{CD}=\frac{BC}{AC-AD}=\frac{BC}{AC-BC}.\]
De esta igualdad, obtenemos que $AC^2-AC\cdot BC-BC^2=0$. Dividiendo entre $AC^2$, llegamos a la ecuación de segundo grado
\[\left(\frac{BC}{AC}\right)^2+\frac{BC}{AC}-1=0\ \Longrightarrow\ \frac{BC}{AC}=\frac{-1\pm\sqrt{5}}{2}.\]
Tenemos que descartar la solución negativa, lo que nos dice finalmente que
\[BC=\frac{\sqrt{5}-1}{2}AC.\]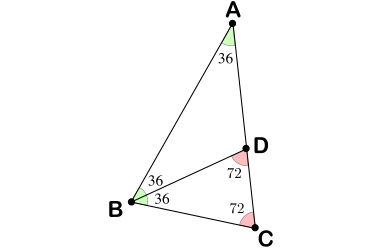
Informar de error en enunciado Informar de procedencia del problema
- El lugar geométrico de $W$ es el conjunto de ecuación $x+y=\frac{k}{2}$ con $x,y,z\gt 0$, es decir, la intersección del plano $x+y=2k$ con el primer cuadrante.
- El lugar geométrico de $W$ es el conjunto de ecuación $x+y=\frac{k}{2}$ y $z=0$ con $x,y\gt 0$, es decir, el segmento de recta que une los puntos $(\frac{k}{2},0,0)$ y $(0,\frac{k}{2},0)$ en el plano $OXY$.
Informar de error en enunciado Informar de procedencia del problema
Nota. Este no es un problema actual de olimpiada ya que apela a un resultado conocido como la desigualdad de Euler. De hecho, en la solución oficial, se menciona solamente que es consecuencia del teorema de Euler que nos dice que la distancia entre el incentro y el circuncentro de cualquier triángulo es $IO^2=R(R-2r)$.
Informar de error en enunciado Informar de procedencia del problema
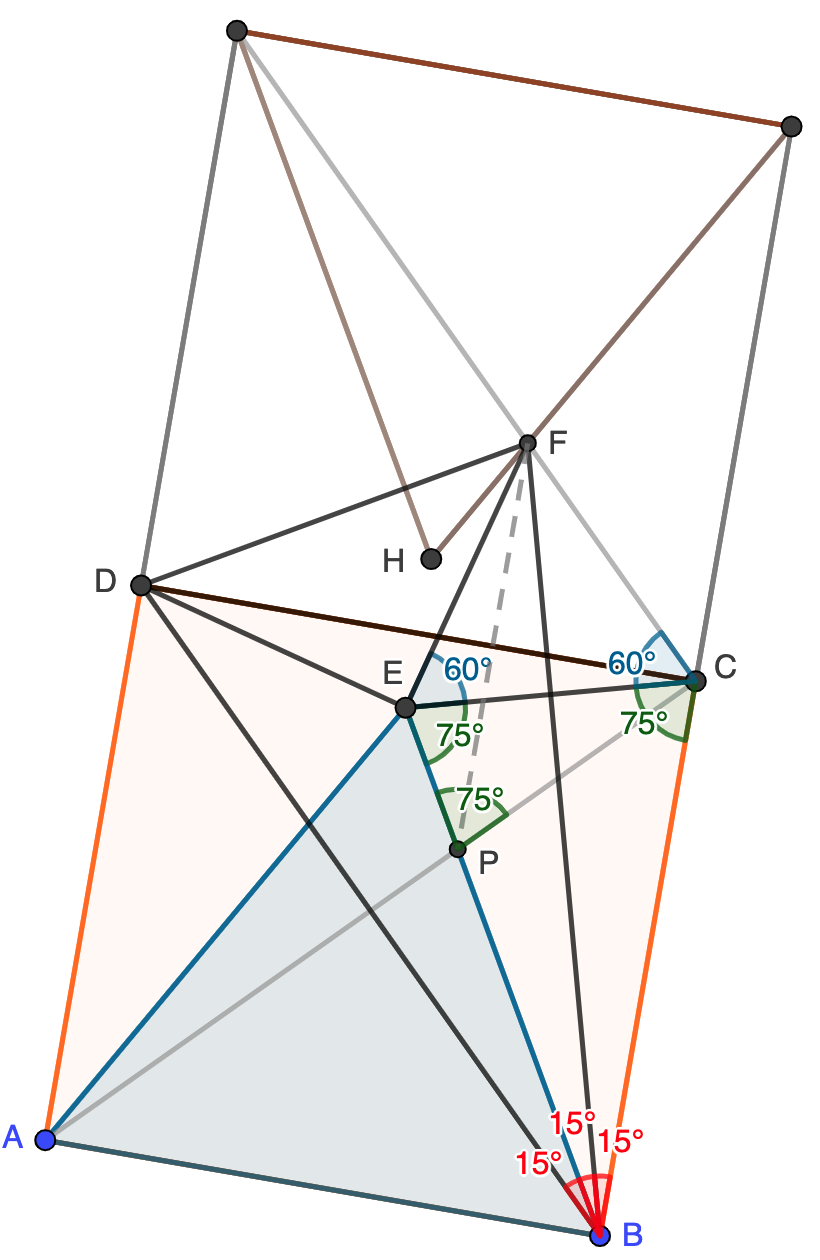
- El triángulo $CEF$ es equilátero.
- El triángulo $DEF$ es rectángulo e isósceles.
- El triángulo $BDF$ es isósceles.
- El triángulo $PDF$ es equilátero.
Que $CEF$ es equilátero implica que $EF=CE=DE$, ya que $CDE$ es claramente isósceles. Además, esto último nos dice que $\angle DEF=180-15-15=150$, con lo que $\angle DEF=150-60=90$. Tenemos entonces probado el apartado (b): $DEF$ es rectángulo e isósceles porque tiene dos lados iguales que forman un ángulo recto.
Ahora observamos que $\angle DEB=60+75=\angle FEB$, luego la recta $EB$ es la bisectriz interior del ángulo recto $\angle DEF$. Esta bisectriz es mediatriz del triángulo isósceles $DEF$, luego cualquier punto de $BE$ está a la misma distancia de $D$ que de $F$. En particular, el triángulo $BDF$ es isósceles y ya tenemos (c).
Tenemos que $PDF$ es isósceles por el mismo motivo, luego será suficiente ver que $\angle DFP=60$ y habremos terminado (hay realmente muchas formas de hacerlo). Como $\angle DBE=60-45=15$, tenemos que $\angle EBF=15$, luego también tenemos que $\angle FBC=90-45-15-15=15$. En otras palabras, $FB$ es bisectriz (y por tanto mediatriz) en el triángulo isósceles $CBE$, luego también lo es del triángulo equilátero $EFC$. Esto nos lleva a que $\angle EFB=\angle BFE=30$. Si trazamos ahora el segmento $PF$, que es paralelo a $BC$ por la simetría, tenemos que $\angle PFB=\angle CBF=15$ por ser ángulos internos alternos, luego $\angle DFP=45+15=60$ como queríamos probar.
Informar de error en enunciado Informar de procedencia del problema
Para ver que el ángulo $x=\angle AMB$ es $45^\circ$, probaremos que su seno al cuadrado es $\frac{1}{2}$ (como $x\lt 90^\circ$, esto termina la demostración). Usando el teorema del seno en el triángulo $ABM$, tenemos que \begin{align*} \frac{c}{\mathrm{sen}(x)}=\frac{m}{\mathrm{sen}(105)}&\ \Longleftrightarrow\ \mathrm{sen}^2(x)=\frac{c^2\,\mathrm{sen}^2(105)}{m^2}=\frac{\frac{1}{2}\cdot\frac{2+\sqrt{3}}{4}}{\frac{2+\sqrt{3}}{4}}=\frac{1}{2}. \end{align*}
Informar de error en enunciado Informar de procedencia del problema