Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Nota. Este no es un problema actual de olimpiada ya que apela a un resultado conocido como la desigualdad de Euler. De hecho, en la solución oficial, se menciona solamente que es consecuencia del teorema de Euler que nos dice que la distancia entre el incentro y el circuncentro de cualquier triángulo es $IO^2=R(R-2r)$.
Informar de error en enunciado Informar de procedencia del problema
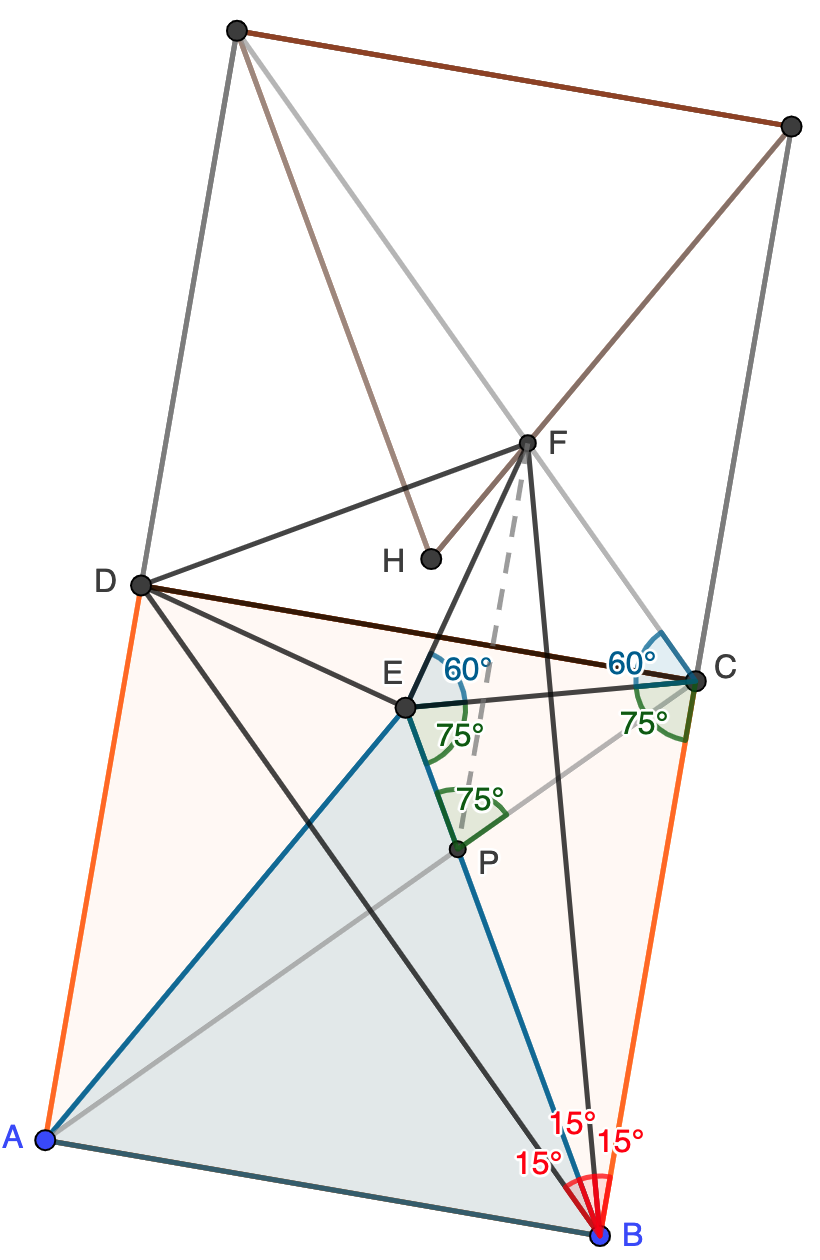
- El triángulo $CEF$ es equilátero.
- El triángulo $DEF$ es rectángulo e isósceles.
- El triángulo $BDF$ es isósceles.
- El triángulo $PDF$ es equilátero.
Que $CEF$ es equilátero implica que $EF=CE=DE$, ya que $CDE$ es claramente isósceles. Además, esto último nos dice que $\angle DEF=180-15-15=150$, con lo que $\angle DEF=150-60=90$. Tenemos entonces probado el apartado (b): $DEF$ es rectángulo e isósceles porque tiene dos lados iguales que forman un ángulo recto.
Ahora observamos que $\angle DEB=60+75=\angle FEB$, luego la recta $EB$ es la bisectriz interior del ángulo recto $\angle DEF$. Esta bisectriz es mediatriz del triángulo isósceles $DEF$, luego cualquier punto de $BE$ está a la misma distancia de $D$ que de $F$. En particular, el triángulo $BDF$ es isósceles y ya tenemos (c).
Tenemos que $PDF$ es isósceles por el mismo motivo, luego será suficiente ver que $\angle DFP=60$ y habremos terminado (hay realmente muchas formas de hacerlo). Como $\angle DBE=60-45=15$, tenemos que $\angle EBF=15$, luego también tenemos que $\angle FBC=90-45-15-15=15$. En otras palabras, $FB$ es bisectriz (y por tanto mediatriz) en el triángulo isósceles $CBE$, luego también lo es del triángulo equilátero $EFC$. Esto nos lleva a que $\angle EFB=\angle BFE=30$. Si trazamos ahora el segmento $PF$, que es paralelo a $BC$ por la simetría, tenemos que $\angle PFB=\angle CBF=15$ por ser ángulos internos alternos, luego $\angle DFP=45+15=60$ como queríamos probar.
Informar de error en enunciado Informar de procedencia del problema
Para ver que el ángulo $x=\angle AMB$ es $45^\circ$, probaremos que su seno al cuadrado es $\frac{1}{2}$ (como $x\lt 90^\circ$, esto termina la demostración). Usando el teorema del seno en el triángulo $ABM$, tenemos que \begin{align*} \frac{c}{\mathrm{sen}(x)}=\frac{m}{\mathrm{sen}(105)}&\ \Longleftrightarrow\ \mathrm{sen}^2(x)=\frac{c^2\,\mathrm{sen}^2(105)}{m^2}=\frac{\frac{1}{2}\cdot\frac{2+\sqrt{3}}{4}}{\frac{2+\sqrt{3}}{4}}=\frac{1}{2}. \end{align*}
Informar de error en enunciado Informar de procedencia del problema
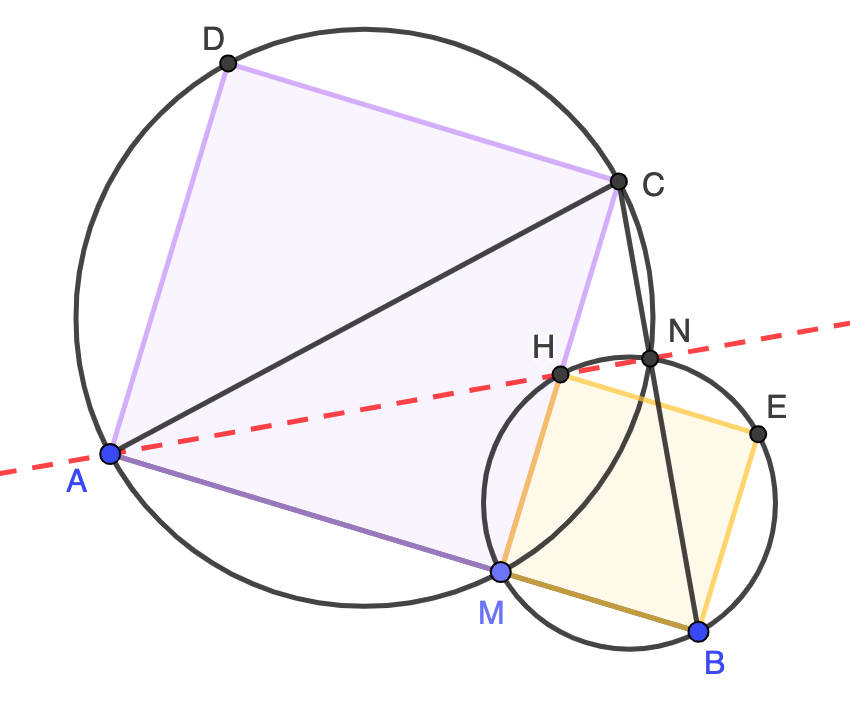
- Probar que los puntos $B$, $N$ y $C$ están alineados.
- Probar que el punto $H$ es el ortocentro del triángulo $ABC$.
- El ángulo $\angle HNB$ es recto ya que $HB$ es un diámetro de la circunferencia circunscrita al cuadrado $MBEH$. Por tanto, tanto $\angle HNB$ como $\angle HNC$ son rectos, lo que nos dice que $B$, $N$ y $C$ están alineados.
- Con lo ya demostrado, tenemos que $AN$ es la altura que pasa por $A$ en el triángulo $ABC$ y es obvio que $CM$ es la altura que pasa por el vértice $C$. Su intersección es $H$ y, por consiguiente, $H$ es el ortocentro de $ABC$.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema