Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
La base de datos contiene 1154 problemas y 775 soluciones.
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |
Problema 720
Sea $M$ un punto interior del segmento $AB$. Se construyen cuadrados $AMCD$ y $BEHM$ en el mismo lado de $AB$. Sea $N$ el punto de intersección (distinto de $M$) de las circunferencias circunscritas a dichos cuadrados.
- Probar que los puntos $B$, $N$ y $C$ están alineados.
- Probar que el punto $H$ es el ortocentro del triángulo $ABC$.
pistasolución 1info
Pista. ¿Qué relación hay entre los triángulos $AMH$ y $CMB$?
Solución. Los dos triángulos $AHM$ y $CMB$ son congruentes por ser rectángulos y tener los catetos iguales (son iguales a los lados de los cuadrados). Además, podemos pasar de $AHM$ a $CMB$ mediante una rotación de $90^\circ$ con centro en $M$, luego la recta $AH$ (en rojo discontinuo) es perpendicular a $BC$. Ahora bien, la recta $BC$ también es perpendicular a $AN$ ya que $AC$ es un diámetro de la circunferencia circunscrita al cuadrado $AMCD$. Por tanto $AN$ y $AH$ son la misma recta, es decir, $A$, $H$ y $N$ están alineados. Respondemos ahora a las dos cuestiones:
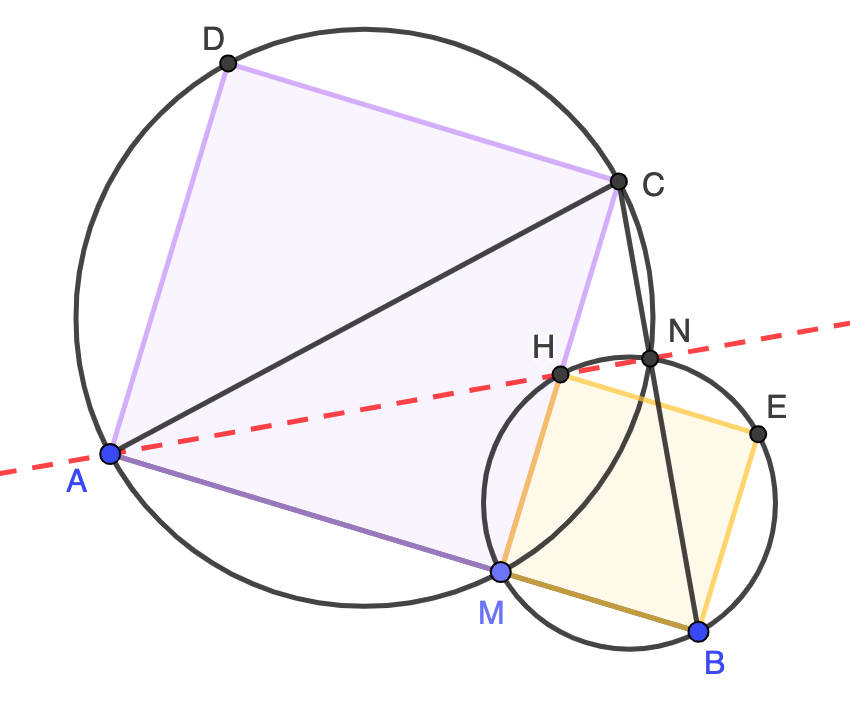
- El ángulo $\angle HNB$ es recto ya que $HB$ es un diámetro de la circunferencia circunscrita al cuadrado $MBEH$. Por tanto, tanto $\angle HNB$ como $\angle HNC$ son rectos, lo que nos dice que $B$, $N$ y $C$ están alineados.
- Con lo ya demostrado, tenemos que $AN$ es la altura que pasa por $A$ en el triángulo $ABC$ y es obvio que $CM$ es la altura que pasa por el vértice $C$. Su intersección es $H$ y, por consiguiente, $H$ es el ortocentro de $ABC$.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 719
En un triángulo $ABC$, las alturas desde los vértice $A$, $B$ y $C$ cortan a las rectas $BC$, $CA$ y $AB$ en los puntos $D$, $E$ y $F$, respectivamente. Las perpendiculares a los lados $AB$ y $AC$ que pasan por $D$ cortan a estos lados en $P$ y $Q$, respectivamente. Las perpendiculares a los lados $BC$ y $AB$ que pasan por $E$ cortan a estos lados en $R$ y $S$, respectivamente. Las perpendiculares a los lados $CA$ y $BC$ que pasan por $F$ cortan a estos lados en $U$ y $V$, respectivamente. Demostrar que hay una circunferencia que pasa por los seis puntos $P,Q,R,S,U,V$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 718
OIM, 1997-P5
En un triángulo acutángulo $ABC$, sean $AE$ y $BF$ dos alturas y sea $H$ el ortocentro. La recta simétrica de $AE$ respecto de la bisectriz interior del ángulo $A$ y la recta simétrica de $BF$ respecto de la bisectriz interior del ángulo $B$ se cortan en un punto $O$. Las rectas $AE$ y $AO$ cortan por segunda vez a la circunferencia circunscrita al triángulo $ABC$ en los puntos $M$ y $N$, respectivamente. Sea $P$ la intersección de $BC$ con $HN$, $R$ la intersección de $BC$ con $OM$ y $S$ la intersección de $HR$ con $OP$. Demostrar que $AHSO$ es un paralelogramo.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 716
OIM, 1997-P2
Con centro en el incentro $I$ de un triángulo $ABC$ se traza una circunferencia que corta en dos puntos a cada uno de los tres lados del triángulo: al segmento $BC$ en $D$ y $P$ (siendo $D$ el más cercano a B) ; al segmento $CA$ en $E$ y $Q$ (siendo $E$ el más cercano a $C$); y al segmento $AB$ en $F$ y $R$ (siendo $F$ el más cercano a $A$). Sea $S$ el punto de intersección de las diagonales del cuadrilátero $EQFR$. Sea $T$ el punto de intersección del cuadrilátero $FRDP$. Sea $U$ el punto de intersección de las diagonales del cuadrilátero $DPEQ$. Demostrar que las circunferencias circunscritas a los triángulos $FRT$ , $DPU$ y $EQS$ tienen un único punto común.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 714
OIM, 1996-P6
Se tienen $n$ puntos distintos $A_1,A_2,\ldots,A_n$ en el plano y a cada punto $A_i$ se le ha asignado un número real $\lambda_i$ distinto de cero, de manera que el cuadrado de la distancia entre $A_i$ y $A_j$ es igual a $\lambda_i+\lambda_j$ para todo $i,j$ con $i\neq j$.
- Demostrar que $n\leq 4$.
- Si $n=4$, demostrar que $\frac{1}{\lambda_1}+\frac{1}{\lambda_2}+\frac{1}{\lambda_3}+\frac{1}{\lambda_4}=0$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2024. Esta página ha sido creada mediante software libre