Olimpiadas de Matemáticas
Página de preparación y problemas

Todos los problemas
Competiciones
| OME Local |
| OME Nacional |
| OIM |
| OME Andalucía |
| Retos UJA |

Informar de error en enunciado Informar de procedencia del problema
De vuelta al problema en cuestión, se trata de ver si el ángulo $\alpha$ opuesto a $ar^2$ es agudo, recto u obtuso. Por el teorema del coseno, este ángulo verifica \[(ar^2)^2=a^2+(ar)^2-2a(ar)\cos(\alpha)\ \Leftrightarrow\ \cos(\alpha)=\frac{1+r^2-r^4}{2r}\] y buscamos saber cuándo esta última cantidad es negativa (obtusángulo), cero (rectángulo) o positiva (acutángulo). Para ello, resolvemos la ecuación bicuadrada $1+r^2-r^4=0$, que nos da soluciones \[r^2=\frac{1\pm\sqrt{5}}{2}\ \Rightarrow\ r=\pm\sqrt{\frac{1+\sqrt{5}}{2}},\] donde hemos descartado las dos soluciones (complejas) en que $r^2$ era negativo. Deducimos que el polinomio $p(r)=1+r^2-r^4$ cambia de signo en estos dos valores (son raíces simples). Como el coeficiente de mayor grado es negativo, $p(r)$ pasa de negativo a positivo y luego a negativo. Tenemos así la solución al problema:
- acutángulo: $1\leq r\lt \sqrt{\frac{1+\sqrt{5}}{2}}$,
- rectángulo: $r=\sqrt{\frac{1+\sqrt{5}}{2}}$,
- obtusángulo: $\sqrt{\frac{1+\sqrt{5}}{2}}\lt r\lt \frac{1+\sqrt{5}}{2}$.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
- Si $P$ y $Q$ están en $S$, entonces $m(PQ)$ corta a $S$.
- Si $P_1Q_1$, $P_2Q_2$ y $P_3Q_3$ son tres segmentos diferentes cuyos extremos son puntos de $S$, entonces no existe ningún punto de $S$ en la intersección de $m(P_1Q_1)$, $m(P_2Q_2)$ y $m(P_3Q_3)$.
Informar de error en enunciado Informar de procedencia del problema
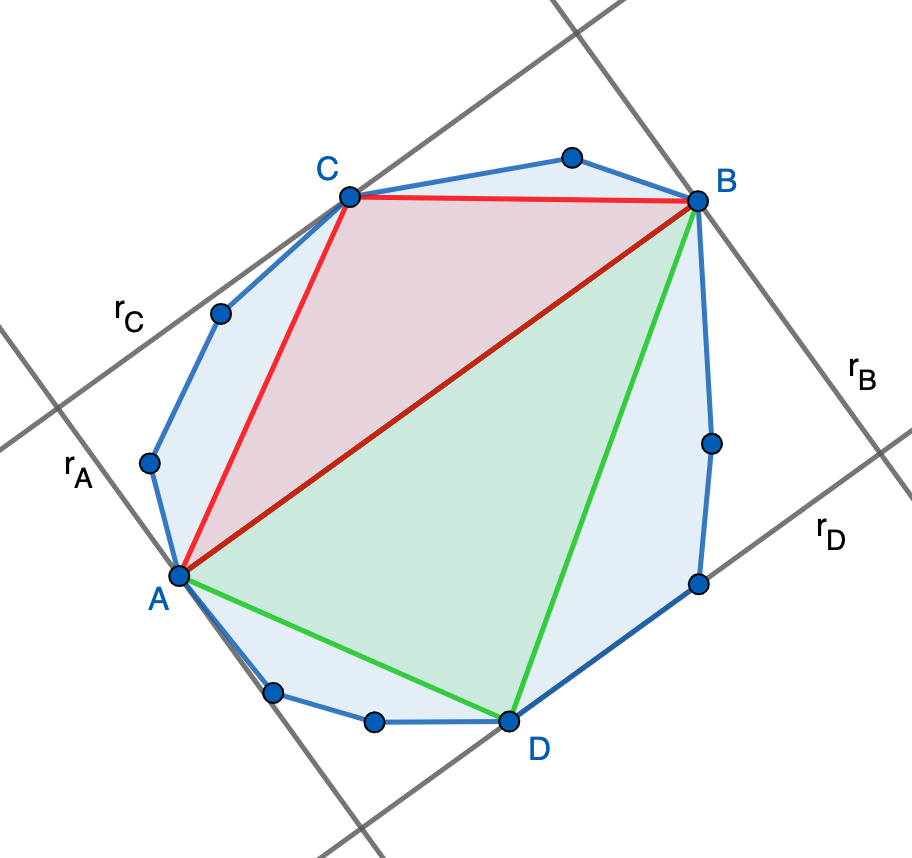
- En primer lugar, tenemos que ningún vértice se puede salir de la banda determinada por $r_A$ y $r_B$ ya que en tal caso dicho vértice tendría distancia con $A$ o con $B$ mayor que $AB$ (¿por qué?), contradiciendo que $AB$ es el segmento entre vértices de longitud máxima. Por otro lado, ningún vértice se puede salir de la banda determinada por $r_C$ y $r_D$ ya que en tal caso dicho vértice distaría de $AB$ más que $C$ o $D$, contradiciendo que estos son los puntos más alejados. Por tanto, todos los vértices del polígono están en $R$ y, por convexidad, todo el polígono debe estar en $R$.
- Finalmente, veamos que $\text{área}(R)\leq 2$. Para ello, observamos que los triángulos $ACB$ y $ADB$ están contenidos en el polígono (de nuevo, por convexidad), de donde \[1=\text{área}(\text{polígono})\geq\text{área}(ACB)+\text{área}(ADB)=\tfrac{1}{2}\text{área}(R).\]
Esto termina la demostración. Es importante observar que uno de los dos puntos $C$ o $D$ podría no estar definido porque no haya vértices a un lado de la recta $AB$. En tal caso, se razona de forma similar usando que $r_C=AB$ o $r_D=AB$.
Informar de error en enunciado Informar de procedencia del problema